Tarjan 求割边

割边

割边还有另一种叫法：桥。

定义

在学习割边的求法前，肯定要了解一下割边的定义：

在一个连通分量中，若删除某一条边，该连通分量就变成了两个，则该边被称作割边。

例如，在下图中，标有红色三角形的就是一条割边。

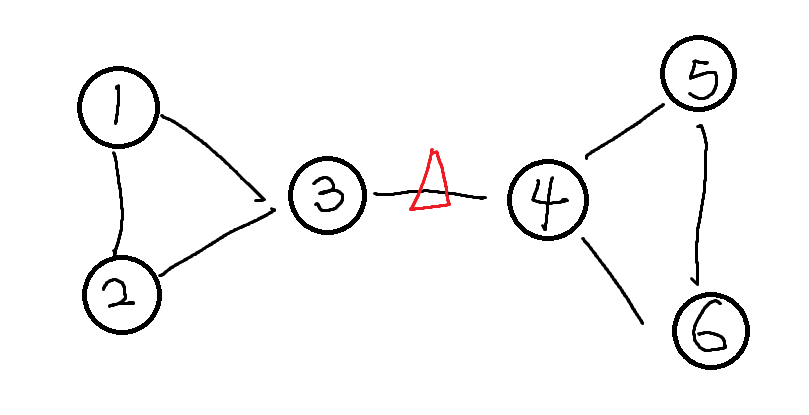
求解方法

前面的强连通分量求解、求割点都用到了 Tarjan 算法，那么在求割边中，是否也能够使用割边呢？答案是肯定的。

先考虑比较简单的情况：无重边。

割边与是否是根节点时没有关系的因为没有根边这种东西（狗头。当一个点 $v$ 不能回到它的祖先也没有另一条能够回到它的父节点 $u$ 的路径，则 $u-v$ 这条边时割边。

代码中把割点代码改成 $lo{w}_v>df{n}_u$。

P1656 炸铁路代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int low[N], dfn[N], idx;
bool isbridge[N];
vector<int> G[N];
int cnt_bridge;
int father[N];
void Tarjan(int u,int fa) 
{
    father[u]=fa;
    low[u]=dfn[u]=++idx;
    for(const auto &v:G[u]) 
    {
        if(!dfn[v]) 
        {
            Tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]) 
            {
                isbridge[v]=true;
                ++cnt_bridge;
            }
        } 
        else if(v!=fa) 
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
}
int m;
struct Edge{
    int x,y;
}bian[N],ans[N];
bool cmp(Edge aa,Edge bb)
{
    if(aa.x==bb.x) return aa.y<bb.y;
    else return aa.x<bb.x;
}
int n; 
int main(){
	cin>>n>>m;
    if(n==10&&m==9)
    {
        cout<<"1 2\n1 3\n1 4\n3 5\n3 6\n3 7\n3 8\n4 9\n4 10";
        return 0;
    }
	for(int i=1; i<=m; i++)
    {
        cin>>bian[i].x>>bian[i].y;
        G[bian[i].x].push_back(bian[i].y);
        G[bian[i].y].push_back(bian[i].x);
    }
	for(int i=1; i<=n; i++)
    {
        if(!dfn[i])
        {
            Tarjan(i,i);
        }
    }
    int cnt_ans=0;
	for(int i=1; i<=m; i++)
	{
		if(isbridge[i]) 
		{
			ans[++cnt_ans]=Edge{father[i],i};
			ans[cnt_ans]=Edge{min(ans[cnt_ans].x,ans[cnt_ans].y),max(ans[cnt_ans].x,ans[cnt_ans].y)};
		}
	}
    sort(ans+1,ans+1+cnt_ans,cmp);
    for(int i=1; i<=cnt_ans; i++)
    {
        cout<<ans[i].x<<" "<<ans[i].y<<"\n";
    }
}	

注：代码中的 $isbridge$ 标记是否为割边，$isbridg{e}_i$ 为 $true$ 则表示节点 $i$ 是割边，否则不是。