HDU 2364 Escape（bfs+三维标记）

Escape

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1228    Accepted Submission(s): 521

Problem Description

You find yourself trapped in a large rectangular room, made up of large square tiles; some are accessible, others are blocked by obstacles or walls. With a single step, you can move from one tile to another tile if it is horizontally or vertically adjacent (i.e. you cannot move diagonally).
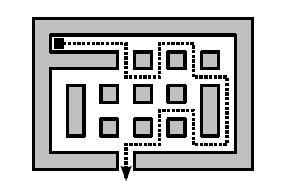
To shake off any people following you, you do not want to move in a straight line. In fact, you want to take a turn at every opportunity, never moving in any single direction longer than strictly necessary. This means that if, for example, you enter a tile from the south, you will turn either left or right, leaving to the west or the east. Only if both directions are blocked, will you move on straight ahead. You never turn around and go back!
Given a map of the room and your starting location, figure out how long it will take you to escape (that is: reach the edge of the room).

 

Input

On the first line an integer t (1 <= t <= 100): the number of test cases. Then for each test case:

a line with two integers separated by a space, h and w (1 <= h, w <= 80), the height and width of the room;

then h lines, each containing w characters, describing the room. Each character is one of . (period; an accessible space), # (a blocked space) or @ (your starting location).
There will be exactly one @ character in each room description.

 

Output

For each test case:

A line with an integer: the minimal number of steps necessary to reach the edge of the room, or -1 if no escape is possible.

 

Sample Input

2

9 13

#############

#@..........#

#####.#.#.#.#

#...........#

#.#.#.#.#.#.#

#.#.......#.#

#.#.#.#.#.#.#

#...........#

#####.#######

4 6

#.####

#.#.##

#...@#

######

 

Sample Output

31

-1

 

这道题在谷歌翻译的帮助下题意是很好理解，思路很清晰，就是敲起来有点麻烦，一下敲了一百八十多行，但是没过样例，把走过的点都输出出来，发现有的时候没拐，想不清之后就搜了博客，博客上代码写的真是少啊，八十多行，九十多行，虽然都是bfs，但是没看懂。通过观察还是有所发现的，别人都是三维标记。题中的不能反向走，我理解错了，我以为走过的不能再走了，这样不就是没有反向了，其实是对于每个点，有四个方向可以到达此点，也就是每个点有四种状态。改了标记数组之后，终于A了~.~  然后又精简了我的代码，虽然比起别人的还是多，但是我的是一步一步来的，都能看懂！

#include<string.h>
#include<stdio.h>
#include<queue>
#include<string>
#include<algorithm>
using namespace std;
int x1,y1;
int n,m;
char mat[85][85];
int vis[85][85][4];
int f[4][2]={0,1,0,-1,-1,0,1,0};//左，右，上，下； 
struct node{
	int x,y;//坐标 
	int ff;//方向 
	int temp;
};
int judge(int a,int b,int c,int d)
{//判断符不符合拐弯的条件 
	if(mat[a][b]=='#'&&mat[c][d]=='#')
	{
		return 0;
	}
	return 1;
}
void bfs()
{
	node s,t;
	queue<node>q;
	s.x=x1;
	s.y =y1;
	s.temp=0;
	s.ff=-1;//起始方向为-1 
	vis[x1][y1][0]=vis[x1][y1][1]=vis[x1][y1][2]=vis[x1][y1][3]=1;
	q.push(s);
	while(!q.empty())
	{
		int flag=0;
		t=q.front();
		q.pop();
		if((t.x==0||t.x==n-1||t.y==0||t.y==m-1))
		{//到达边缘 
			printf("%d\n",t.temp );
			return;
		}
		int x2,x3,y2,y3;
		if(t.ff==0||t.ff==1)
		{//当从左，或从右到达t点时，判断上下方向能不能拐弯 
			x2=t.x+1;
			y2=t.y;
			x3=t.x-1;
			y3=t.y;
			if(judge(x2,y2,x3,y3))
			{//如果能拐
				for(int i=2;i<4;i++)
				{//向上或向下拐 
					s.x=t.x+f[i][0];
					s.y=t.y+f[i][1];
					s.temp=t.temp+1;
					s.ff=i;//记录s点从哪个方向过来的 
					if(s.x>=n||s.x<0||s.y>=m||s.y<0||vis[s.x][s.y][s.ff]||mat[s.x][s.y]=='#')
						continue;
					vis[s.x][s.y][i]=1;
					q.push(s);	
				}
			}
			else flag=1;//不能拐，标记 
		}
			
		else if(t.ff==3||t.ff==2)
		{//从上或下到达t点时，判断左右方向能不能拐弯 
			x2=t.x;
			y2=t.y+1;
			x3=t.x;
			y3=t.y-1;
			if(judge(x2,y2,x3,y3))
			{//能拐 
				for(int i=0;i<2;i++)
				{//就两个方向，向左或向右拐 
					s.x=t.x+f[i][0];
					s.y=t.y+f[i][1];
					s.temp=t.temp+1;
					s.ff=i;
					if(s.x>=n||s.x<0||s.y>=m||s.y<0||vis[s.x][s.y][s.ff]||mat[s.x][s.y]=='#')
						continue;
					vis[s.x][s.y][s.ff]=1;
					q.push(s);
				}
			}
			else flag=1;//不能拐，标记 
		}
		
		else if(t.ff==-1)
		{//这是起点的时候，任意方向都可以 
			for(int i=0;i<4;i++)
			{
				s.x=t.x+f[i][0];
				s.y=t.y+f[i][1];
				s.temp=t.temp+1;
				s.ff=i;
				if(s.x>=n||s.x<0||s.y>=m||s.y<0||vis[s.x][s.y][s.ff]||mat[s.x][s.y]=='#')
					continue;
				vis[s.x][s.y][s.ff]=1;
				q.push(s);	
			}
		}
		
		if(flag==1)
		{//如果不能拐，就按原方向前进 
			s.x=t.x+f[t.ff][0];
			s.y=t.y+f[t.ff][1];
			s.temp=t.temp+1;
			s.ff=t.ff;
			if(s.x>=n||s.x<0||s.y>=m||s.y<0||vis[s.x][s.y][s.ff]||mat[s.x][s.y]=='#')
				continue;
			vis[s.x][s.y][s.ff]=1;
			q.push(s);
		}
	}
	printf("-1\n");
	return;
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		memset(vis,0,sizeof(vis));
		scanf("%d%d",&n,&m);
		for(int i=0;i<n;i++)
			scanf("%s",mat[i]);
		for(int i=0;i<n;i++)
			for(int j=0;j<m;j++)
			{
				if(mat[i][j]=='@')
				{//起点 
					x1=i;y1=j;
				}
			}
			if(x1==0||x1==n-1||y1==0||y1==m-1)
			{//起点在边缘，就是0 
				printf("0\n");
				continue;
			}
			bfs();
	}
	return 0; 
}