深入解析生成式大语言模型中的激活函数：从ReLU到SiLU，理解神经网络的核心组件！

最新推荐文章于 2025-12-13 20:58:45 发布

原创最新推荐文章于 2025-12-13 20:58:45 发布 · 771 阅读

34 ·

CC 4.0 BY-SA版权

文章标签：

#语言模型 #神经网络 #人工智能 #transformer #深度学习 #自然语言处理 #大模型学习

激活函数是神经网络中的核心组件，它决定了神经元是否被激活以及如何将输入信号转换为输出信号，也是将神经网络引入非线性表达能力的关键组件。

在大型语言模型（LLM）中，用于引入非线性变换，使模型能够学习复杂的模式和关系。

它们在模型的每一层（尤其是前馈网络部分）中起核心作用，直接影响模型的表达能力和训练效果。趁着最近在学习生成式 LLM 的契机，分享自己对激活函数的理解和思考。

本文主要介绍现在主流生成式 LLM 所用的激活函数：ReLU（GPT2 中使用，现在主流 LLM，如 llama3、DeepSeek 等不再使用，但是它是其他激活函数的改进的源头，所以个人认为有必要介绍，如有熟知的同学自行跳过），GELU、Sigmod-GELU（是 GELU 的近似版本）、Swish、SiLU（是 Swish 的特例）。

一、ReLU

ReLU（Rectified Linear Unit，修正线性单元）是一种广泛使用的激活函数，尤其在深度学习中表现优异，它的数学形式非常简单，但在神经网络中解决了传统激活函数（如 Sigmoid、Tanh）的一些关键问题。

如计算复杂、输入值的绝对值较大的区域（即饱和区）容易发生梯度消失等问题。

ReLU 的数学表达式如下：

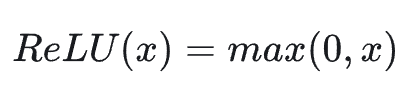
当输入 x≥0 时，输出为 x，否则输出为 0。

ReLU 的梯度数学表达式如下：

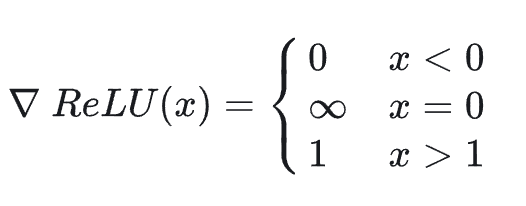
由此可知，当输入 x 小于 0 时，梯度为 0，即发生梯度消失，当输入 x 为 0 时，梯度为无穷大，梯度爆炸，输入 x 大于 0 时，梯度为 1。

（1）ReLU 图像和梯度图像

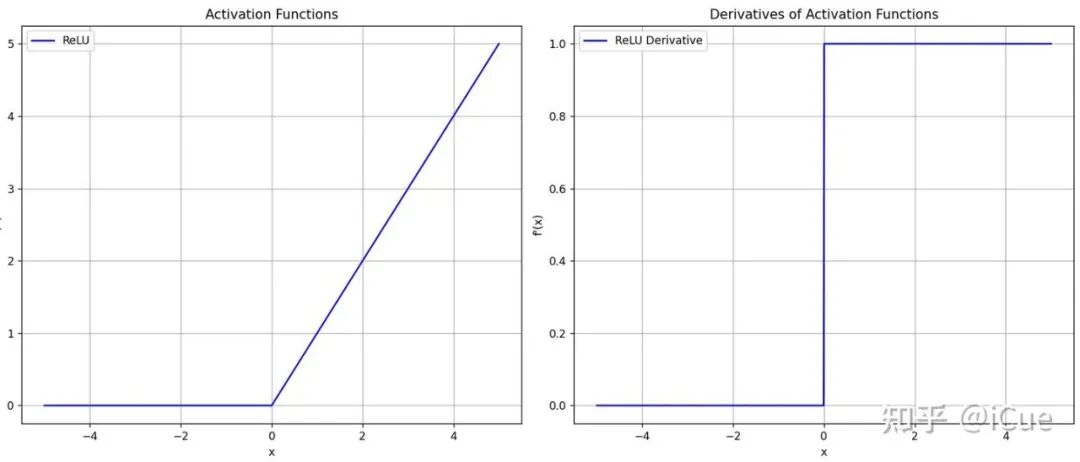
ReLU 图像和梯度图像

ReLU 优点：

计算高效：ReLU 的计算仅需判断输入是否大于零，没有复杂的指数运算（如 Sigmoid/Tanh），因此在训练和推理时速度极快
缓解梯度消失问题：传统激活函数（如 Sigmoid）在输入较大或较小时会进入“饱和区”，梯度接近零，导致反向传播时梯度消失（Vanishing Gradient，ReLU 在正区间（x>0）的梯度恒为 1，避免了梯度消失问题，使得深层网络更容易训练
稀疏激活：ReLU 会使负值输入直接输出零，导致神经元的“稀疏激活”（部分神经元不激活）。这种特性可以：减少参数之间的依赖性，增强模型的泛化能力
生物学合理性：ReLU 的稀疏激活特性类似于生物神经元的“全或无”（All-or-None）激活模式，被认为更接近人脑的工作机制。

ReLU 缺点：

神经元死亡（Dead Neurons）：当输入为负数时，ReLU 的梯度为零。如果某个神经元在训练中始终输出负数（例如权重初始化不当或学习率过高），其梯度将永远为零，导致该神经元永久失效（“死亡”）, 这种现象称为 Dying ReLU Problem。
非零中心化：ReLU 的输出范围为 [0,+∞)，导致激活值的分布不对称（非零中心化），可能影响梯度下降的效率。

（2）ReLU 使用注意事项

如下：

权重初始化：建议使用 He 初始化（针对 ReLU 设计），以缓解神经元死亡问题；
学习率调整：过高的学习率可能导致大量神经元死亡，需谨慎选择；
结合 Batch Normalization：可以进一步稳定训练过程。

二、GELU

GELU（Gaussian Error Linear Unit，高斯误差线性单元）是一种近年来被广泛使用的激活函数，尤其在 Transformer 架构（如BERT、GPT）中表现优异。

它结合了随机正则化的思想，通过概率权重对输入进行非线性变换，比传统激活函数（如 ReLU、Sigmoid）更符合神经网络的概率特性，有点类似于自适应的 Dropout 机制，因此 LLM 广泛使用类似这种激活函数或其变体。

数学公式定义如下：

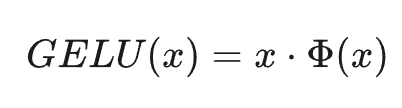
其中：Φ(x) 是标准高斯分布（正态分布）的累积分布函数(CDF)，即 Φ(x)=P(X≤x)，X∼N(0,1)，由于高斯分布计算较为复杂，一般会使用如下第二个公式来近似。

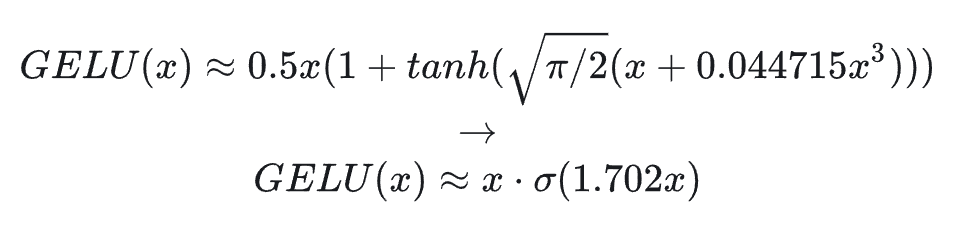
其中 Φ(x) 是标准正态分布的累积分布函数 (CDF)，ϕ(x) 是标准正态分布的概率密度函数（PDF），它的梯度表达如下：

GELU 梯度表达式如下：

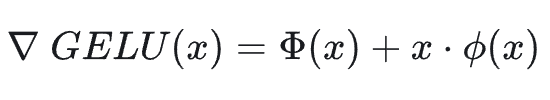
其中 Φ(x) 表示输入 x被激活的概率权重，x⋅ϕ(x) 是输入对概率密度的动态调整项。

（1）GELU 图像和梯度图像

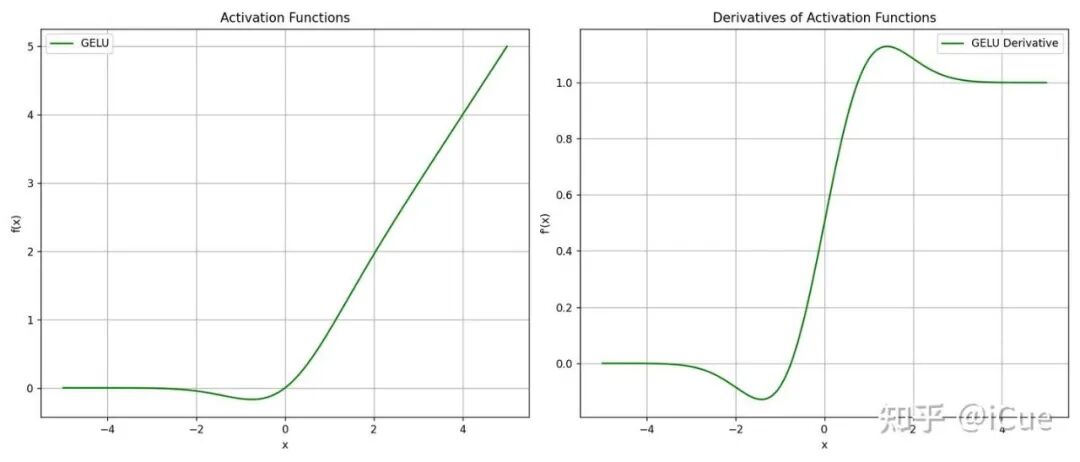
GELU 的图像和梯度图像

（2）GELU 的理解

概率视角：GELU将输入 x 的激活权重与其在正态分布中的概率相关联。

例如：

当 x 较大时，神经元以高概率被激活（输出接近 x）
当 x 较小时，神经元以低概率被激活（输出接近 0）

随机正则化：GELU 的非线性可以被视为一种“自适应 Dropout”，其权重由输入自身决定，而非固定概率。

GELU 优点：

平滑性：GELU 在输入接近零时是连续可导的（与 ReLU 的硬截断不同），这使得梯度更新更稳定
自适应激活：激活权重 Φ(x) 随输入动态调整，能更好地捕捉复杂模式
概率解释：结合正态分布的 CDF，GELU 更符合神经网络的概率建模特性（如贝叶斯网络）
在 Transformer 中的表现：GELU 在自然语言处理（NLP）任务中表现优异，尤其在 BERT、GPT 等模型中，相比 ReLU 和 Swish 函数效果更好

GELU 缺点：

计算成本较高: 精确计算 Φ(x) 需要积分运算，尽管近似方法（如 tanh 或 Sigmoid）可以缓解这一问题
可解释性较弱：相比 ReLU 的直观截断，GELU 的概率权重机制需要更深入的理论理解

这份完整版的大模型 AI 学习和面试资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】
在这里插入图片描述

三、Sigmod-GELU

Sigmoid-GELU 是 GELU（高斯误差线性单元）的一种近似实现方式，通过 Sigmoid 函数替代高斯分布的累积分布函数（CDF），简化计算并保持 GELU 的核心特性。

它就是上面 GELU 介绍中的及时方式，它结合了 Sigmoid 的平滑性和 GELU 的概率权重机制，广泛应用于需要高效计算的场景（如 Transformer 模型）。

其数学表达式如下：

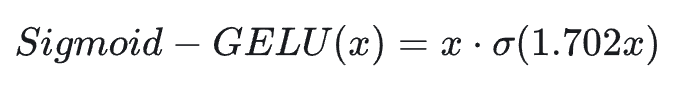
其中 σ(⋅) 是 Sigmoid 函数，系数 1.702 用于调整 Sigmoid 函数的陡峭度，1.702 是一个经验值，使其更接近 GELU 中高斯 CDF 的形状。

Sigmod-GELU 的梯度表达式如下：

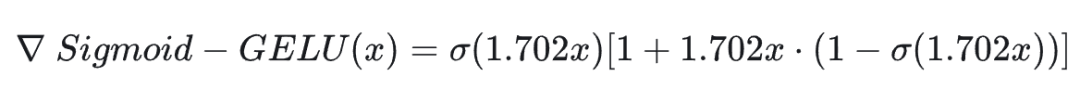
（1）Sigmod-GELU 的图像和梯度图像

Sigmod-GELU 的图像和梯度图像

Sigmod-GELU 的理解：

Sigmoid-GELU 通过 Sigmoid 函数模拟 GELU 的概率权重机制
当输入 x 较大时，σ(1.702x)≈1，输出接近 x
当输入 x 较小时，σ(1.702x)≈0，输出接近 0
在中间区域，输出平滑过渡，保留了 GELU 的非线性特性

（2）为什么要使用 Sigmod-GELU 来近似 GELU

原始 GELU 的公式为 x⋅Φ(x)，其中 Φ(x) 是标准正态分布的 CDF，计算复杂（需积分运算）。

Sigmoid-GELU 的提出是为了：

降低计算成本：Sigmoid 函数可通过指数运算快速计算，适合硬件加速
保持性能：实验表明，当系数 1.702 时，Sigmoid-GELU 与原始 GELU 的拟合误差极小

Sigmod-GELU 的优点：

平滑非线性：输出在正负区间均平滑可导，梯度稳定，适合深度网络训练
自适应概率权重：权重 σ(1.702x) 随输入动态调整，既保留 ReLU 的稀疏性，又避免硬截断
高效计算：仅需一次 Sigmoid 运算和乘法，比精确计算高斯 CDF 快得多
兼容性：在 Transformer、BERT 等模型中可直接替换原始 GELU，无需调整超参数

Sigmod-GELU 的缺点：

系数 1.702 需要经验设定，缺乏理论推导
Sigmoid 函数在极端值时梯度仍可能消失
相比 ReLU，计算量略高，因为需计算 Sigmoid

四、Swish

Swish 是由 Google 研究人员在 2017 年提出的一种激活函数，结合了 Sigmoid 的平滑性和 ReLU 的稀疏激活特性。

实验证明其在多种任务中优于 ReLU，尤其在深层网络中表现优异，也是现在主流 LLM（如 llama、Qwen、DeepSeek）中 FeedForward 层使用的激活函数。

只是它们使用的是 Swish-1，即接下来要解释得 SiLU 激活函数，其数学表达式如下：

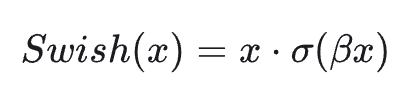
其中 σ(⋅) 是 Sigmoid 函数，β是一个可学习参数或固定常数（默认 β=1）, 当 β=1 时，Swish 激活函数就是接下来要说的 SiLU 激活函数，Swish 梯度表达式如下：

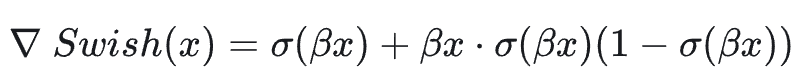
当 x>0 时，导数接近 1（类似 ReLU），当 x<0 时，导数由 β控制，非零且平滑，正是因为当 x<0 时，导数由 β控制，则可以解决 ReLU 激活函数在输入值小于 0 时的梯度消失问题。

（1）Swish 的图像和梯度图像

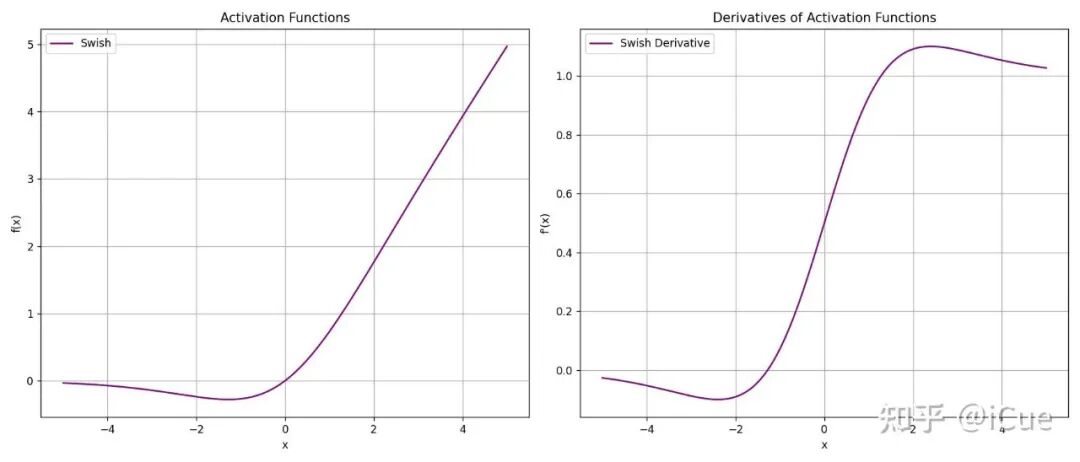
Swish 的图像和梯度图像

Swish 的理解：

Swish 对输入 x 进行 Sigmoid 加权，输出范围为 (−0.278,+∞)
当 β→0 时，Swish 退化为线性函数 x / 2
当 β→+∞ 时，Swish 趋近于 ReLU（x⋅σ(βx)≈x⋅阶跃函数）

Swish 的优点：

平滑非单调性（Smooth Non-Monotonicity）
—非单调性：当 x<0 时，Swish 可能先减小后增大，与 ReLU 的硬截断不同
----平滑性：Swish 处处可导，梯度变化连续，缓解了 ReLU 在 x=0 处的梯度突变问题
自适应性
----通过调整 β，Swish 可以灵活适应不同任务：
----大 β：接近 ReLU，适合需要稀疏激活的任务（如分类）
----小 β：接近线性，适合需要保留更多信息的任务（如回归）
缓解梯度消失
----在负区间（x<0），Swish 的梯度非零，避免了 ReLU 的“神经元死亡”问题
输出非零中心化
----Swish 的输出均值为正（类似 ReLU），可能需搭配 Batch Normalization 使用以加速训练

Swish 的缺点：

计算成本略高于 ReLU（需计算 Sigmoid）
输出非零中心化，需配合 BatchNorm 使用

五、SiLU

SiLU（Sigmoid Linear Unit），也称为 Swish-1，是一种结合了 Sigmoid 函数平滑性和 ReLU 稀疏激活特性的激活函数。

它由 Swish 激活函数的特定形式演化而来（固定参数 β=1）,现在主流 LLM 的 FeedForward 模块中的激活函数都在使用 SiLU 作为激活函数。

其数学表达式如下：

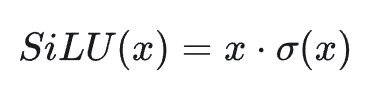
其中 σ(x) 是 Sigmoid 函数，它对应的梯度表达式如下：

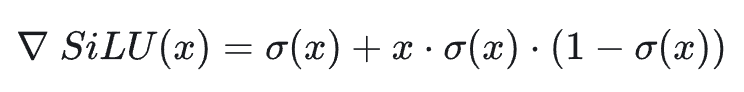
通过 SiLU 激活函数可以得出：正区间（x≫0）：导数 ≈1(类似 ReLU)；负区间（x≪0）：导数 ≈0，但非零，保留微弱梯度；零点附近（x≈0）：导数约为 0.5，梯度平滑过渡。

（1）SiLU 的图像和梯度图像

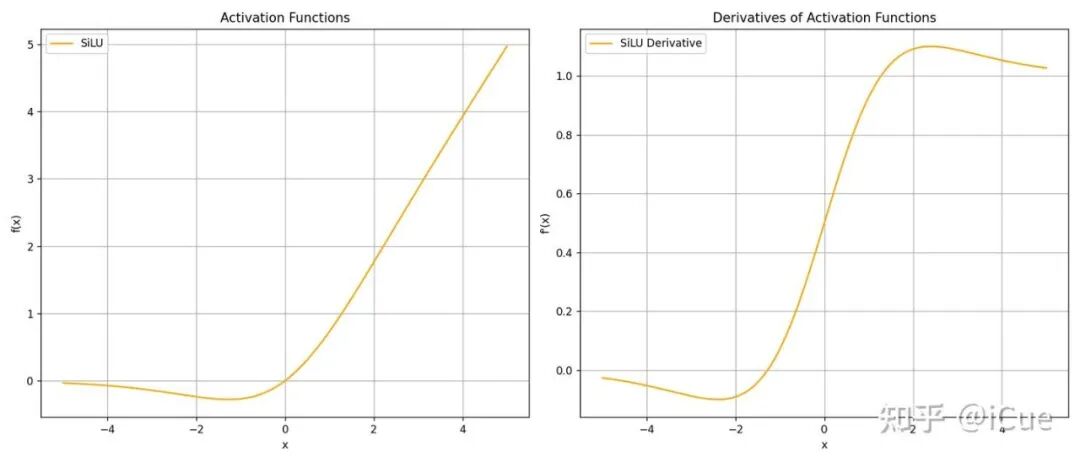
SiLU 的图像和梯度图像

SiLU 的理解：

SiLU 对输入 x 进行 Sigmoid 加权，输出范围为 (−0.278,+∞)
正区间（x>0）：输出接近线性增长（类似 ReLU）
负区间（x<0）：输出平滑衰减至负值，而非直接归零
零点附近（x≈0）：梯度连续，避免硬截断

SiLU 的优点：

平滑性与非单调性
—平滑性：SiLU 在所有输入点处连续可导，梯度更新更稳定
—非单调性：当 x<0 时，SiLU 的输出先减小后增大（极小值约在 x≈−1.278 处），增强了非线性表达能力
缓解梯度消失与神经元死亡
—负区间梯度保留：即使 x<0，梯度仍非零避免 ReLU 的神经元死亡问题
—自适应激活：通过 Sigmoid 权重动态调整激活强度，平衡信息保留与稀疏性
输出非零中心化
—输出均值偏向正区间（类似 ReLU），可能需搭配 Batch Normalization 以加速训练收敛

SiLU 的缺点：

计算成本略高于 ReLU（需计算 Sigmoid）
输出非零中心化，需配合 BatchNorm 使用

ReLU/GELU/Sigmod-GELU/SiLU 的图像和梯度图像绘制 Python 代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Define the activation functions
def relu(x):
return np.maximum(0, x)
def gelu(x):
return x * norm.cdf(x)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_gelu(x):
return x * sigmoid(1.702 * x)
def swish(x, beta=1):
return x * sigmoid(beta * x)
def silu(x):
return swish(x, beta=1)  # SiLU is Swish with beta=1
# Define the derivatives
def relu_derivative(x):
return np.where(x > 0, 1, 0)
def gelu_derivative(x):
return norm.cdf(x) + x * norm.pdf(x)
def sigmoid_derivative(x):
s = sigmoid(x)
return s * (1 - s)
def sigmoid_gelu_derivative(x):
s = sigmoid(1.702 * x)
return s + 1.702 * x * s * (1 - s)
def swish_derivative(x, beta=1):
s = sigmoid(beta * x)
return s + beta * x * s * (1 - s)
def silu_derivative(x):
return swish_derivative(x, beta=1)
# Generate x values
x = np.linspace(-5, 5, 1000)
# Create the figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# Plot activation functions
ax1.plot(x, relu(x), label='ReLU', color='blue')
ax1.plot(x, gelu(x), label='GELU', color='green')
ax1.plot(x, sigmoid_gelu(x), label='Sigmoid-GELU', color='red')
ax1.plot(x, swish(x), label='Swish', color='purple')
ax1.plot(x, silu(x), label='SiLU', color='orange')
ax1.set_title('Activation Functions')
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.grid(True)
ax1.legend()
# Plot derivatives
ax2.plot(x, relu_derivative(x), label='ReLU Derivative', color='blue')
ax2.plot(x, gelu_derivative(x), label='GELU Derivative', color='green')
ax2.plot(x, sigmoid_gelu_derivative(x), label='Sigmoid-GELU Derivative', color='red')
ax2.plot(x, swish_derivative(x), label='Swish Derivative', color='purple')
ax2.plot(x, silu_derivative(x), label='SiLU Derivative', color='orange')
ax2.set_title('Derivatives of Activation Functions')
ax2.set_xlabel('x')
ax2.set_ylabel("f'(x)")
ax2.grid(True)
ax2.legend()
# Adjust layout and display
plt.tight_layout()
plt.show()

输入结果如下：

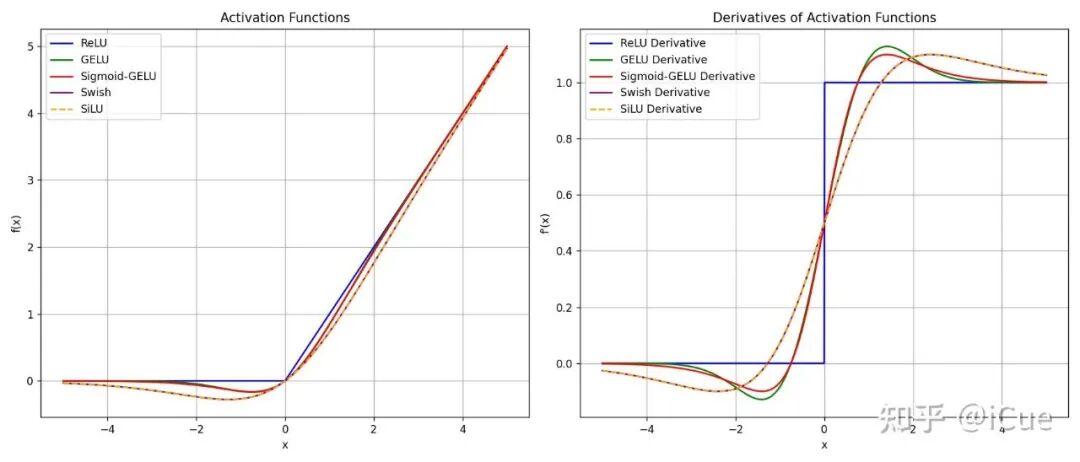
ReLU/GELU/Sigmod-GELU/SiLU 的图像和梯度图像

六、如何学习AI大模型？

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

在这里插入图片描述