【AI大模型面试题】Llama为何要采用RoPE旋转位置编码？

前言

最近在做 LLM 窗口外推的相关工作，因此刚好也回顾一下目前最流行的位置编码 RoPE。

1、关于RoPE

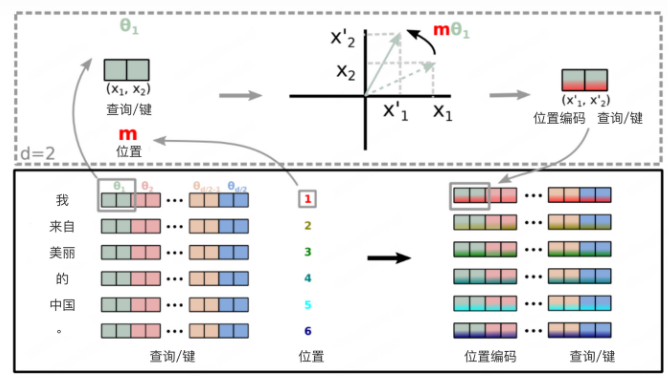
RoPE（Rotary Position Embedding），是苏剑林大神在 2021 年就提出的一种 Transformer 模型的位置编码。

RoPE 是一种可以以绝对位置编码形式实现的相对位置编码，兼顾了模型性能和效率。

2023 年上半年的时候，大模型位置编码尚有 Alibi 和 RoPE 在相互比拼，而到了 2023 年下半年，及今 2024 年，新开源出来的模型，大部分都是使用 RoPE 了。当然 Alibi 也有其优势，这个在讲 Alibi 的时候来说。

苏神在他的个人网站科学空间中对 RoPE 有相关文章进行了介绍，本篇是在这个基础上，对 RoPE 进行理解（公式和符号上也会沿用苏神的写法）。

2、以绝对位置编码的方式实现相对位置编码

前面提到，RoPE 是一种一绝对位置编码的方式实现的相对位置编码，那么这么做能带来什么收益？

先说原因：

在文本长度不长的情况下（比如 Bert 时代基本都是 256/512 token 的长度），相对位置编码和绝对位置编码在使用效果上可以说没有显著差别。

如果要处理更大长度的输入输出，使用绝对位置编码就需要把训练数据也加长到推理所需长度，否则对于没训练过的长度（训练时没见过的位置编码），效果多少会打些折扣。

而使用相对位置编码则更容易外推，毕竟 token-2 和 token-1 的距离，与 token-10002 和 token-10001 的距离是一样的，也因此可以缓解对巨量长文本数据的需求。

但是传统相对位置编码的实现相对复杂，有些也会有计算效率低的问题。由于修改了 self-attention 的计算方式，也比较难推广到线性注意力计算法模型中。

总结来说，就是绝对位置编码好实现，效率高，适用线性注意力，而相对位置编码易外推，因此就有了对“绝对位置编码的方式实现相对位置编码”的追求，去把二者的优点结合起来。

下面简单回顾一下绝对位置编码和相对位置编码。（对位置编码比较熟悉的朋友可以直接跳到第3节。）

（1）绝对位置编码

先回顾一下带绝对位置编码的 self-attention。

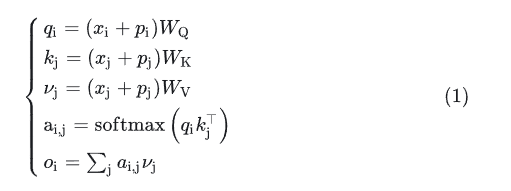
（2）相对位置编码

直观来说，比如词表大小是 1 万，模型训练窗口最大长度是 512，那么对于模型来说，实际上要区分的输入是 1 万×512=512 万个。

看起来虽然不少，但是在海量的数据和训练量下，这也不算什么事儿，模型确实能 handle。

Google 式

为什么要增加一个 clip 操作？因为直观上，一个词对其左右附近的其他词的位置关系理应更加敏感。

比如“我请你吃饭”中，“吃饭”这个词需要以高分辨率明确区分出前面三个词“我”、“请”、“你”的位置，以免理解成了“你请我吃饭”。

而随着距离越来越远，这种高分辨率的需求也就越来越低，十万个 token 之前的内容顺序对于当前 token 来说，影响比较小了，在位置向量上可以一视同仁。

另外这也是方便了位置信息的外推，比如我们可以只训练 256 个相对位置编码信息，而在应用是可以外推到>256 的长度。

本来到这里就可以了，相对位置信息已经加入了，但是 Google 除了在 input 端增加了相对位置信息，在输出端也增加了相对位置信息。

本来输出端的计算是：

XLNET 式

XLNET 也使用了相对位置编码，思路类似 Google，只是具体的操作不同。

在公式（2）的基础上继续展开：

把绝对位置相关的几个参数改成相对位置相关的参数，变成：

此外，XLNET 只对输入端做了处理，输出端则直接把位置相关的计算去掉了，即：

当然，也有简单一点的实现，比如 T5 的方法。

T5 式

（从最早提出，到 XLNET，以及 DeBerta，T5 等，可以看到相对位置编码的实现有一个简化的趋势，而效果也越来越好，正所谓大道至简，有时候有用的东西未必需要很复杂）

（3）对比

看来相对位置编码确实比较复杂，说个大概需要这么多篇幅；并且相对绝对位置编码，也没有那么直接明了，需要对 attention 计算做一些改造。

公式（1）的绝对位置编码中，可以看到在进 softmax 操作前需要做 3 次矩阵加法，3 次矩阵乘法。

从公式（8）可以看到，共有 4 组矩阵计算要做，每组要做 3 次矩阵乘法，相对会比较复杂。

公式（3）也有类似的情况。当然同时也有一些针对相对位置编码的高效计算被提出，这些就需要针对不同的计算方案来优化了。

总之在实现方式上和计算效率上，绝对位置编码具有一些优势。而在输入输出窗口外推方面，相对位置编码有着天然的优势。

另外，绝对位置编码保持 self-attention 的经典形式，使得应用面更广，如可以使用到 linear attention 方案中去，这个以后再展开讲（又挖了个坑）。

3、RoPE的设计思路

（1）保持 attention 计算形式

回顾完经典的绝对位置编码和相对位置编码，回到 RoPE 上来。

先说设计思路：

首先我们想要保持经典 self-attention 的计算方式，即公式（1）中的形式，输入端 = 内积 + softmax，至于输出端则保持完全不变。softmax 我们不去动，那这里留给我们操作的就是内积。

也就说，现在问题是，我们怎么在只做内积的情况下，把内积结果变成只和相对位置有关，而和绝对位置无关的结果。

写成公式就是：

当然理论上这里是存在无数多组答案的，那么 RoPE 怎么找到一组好实现的组合呢？

（2）借用复数寻找组合

这里先回顾一下复数的知识。任意复数都可以表示成复平面的一个 2 维向量。

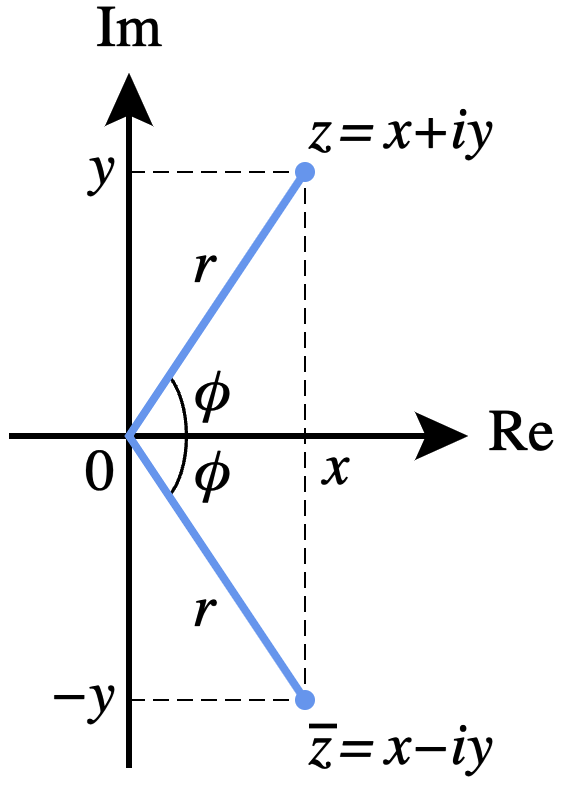
现在考虑 query 和 key 向量都是 2 维的情况，那么可以代入复数的操作。

（先把 hidden size = 2 的情况推理清楚，后续再推广到更高维的情况）

那么在 2 维复数平面上有什么操作可以满足公式（11）的要求呢？Roformer 论文中提出的是这组：

先证明一下这个组合的正确性，是不是真的满足公式（11）。（也可以先跳过证明，选择先相信这个组合）

回顾一下欧拉公式：

（这里沿用式（1）中，默认向量为行向量的设定，所有有个 transpose，实际上是行向量还是列向量都没关系，只是推算的时候写法问题）

类似地，有：

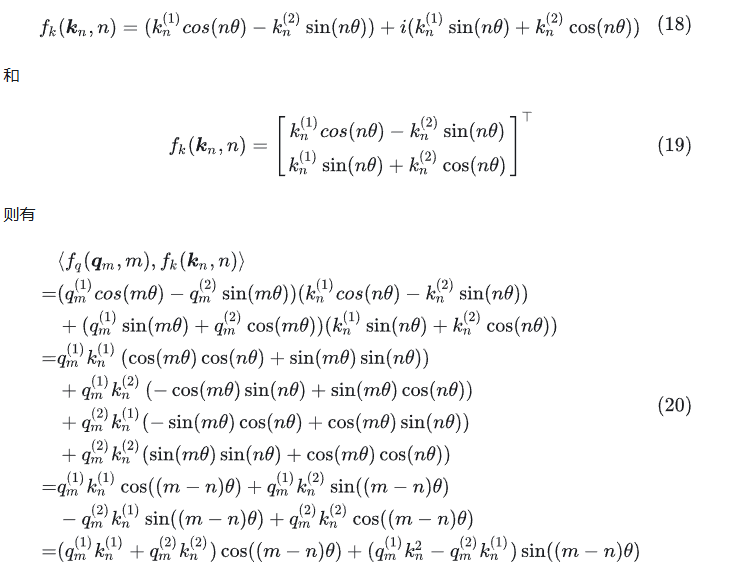
用了三角函数和差公式：

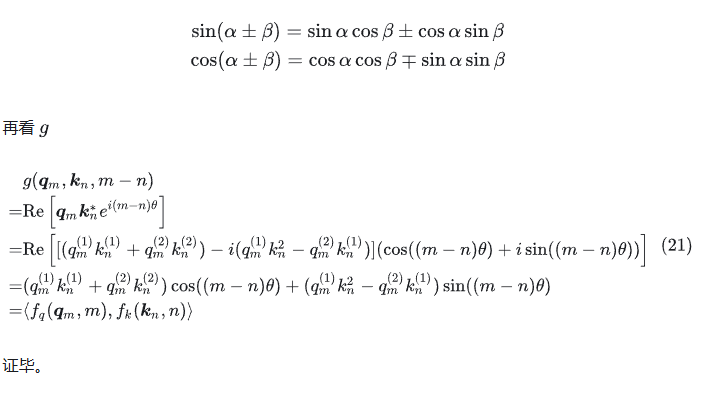
（3）“旋转”位置编码

发现式（17）可以写成这样：

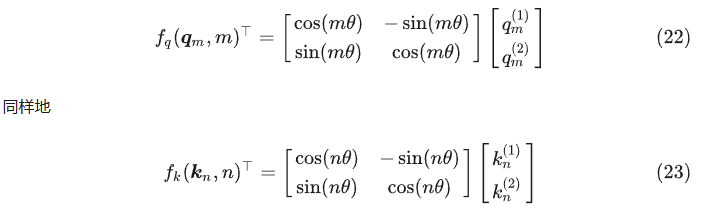
如果从向量视角来看，则有：

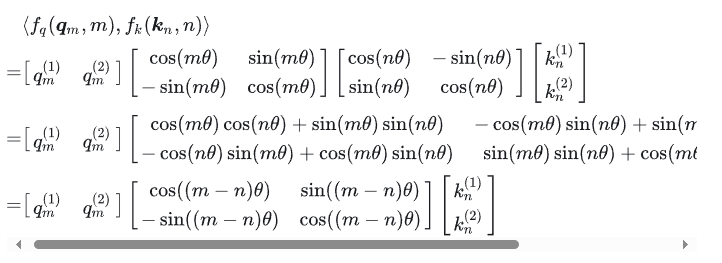
看式（22）和（23），可以看到等号右边都有：

这也是为什么叫做“旋转”位置编码。

（4）从 2 维推广到高维

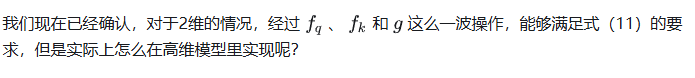
答案是把高维输入拆分成两个两个一组（这要求输入是偶数维，目前的模型也都是偶数维，所以没问题），则高维的“旋转”矩阵有多个小旋转矩阵组成。

（5）高效率实现

式（25）中的矩阵在高维的情况下很稀疏，直接使用这么个矩阵来计算效率并不高，可以使用一个这样的高效率实现方式。

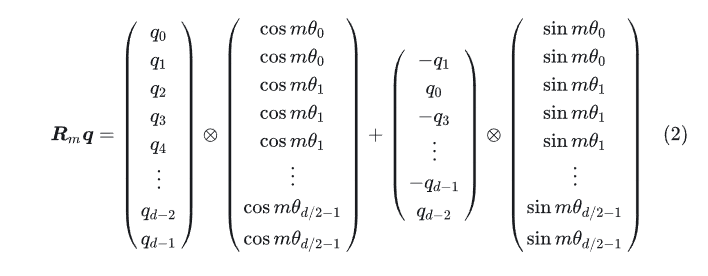
只需进行两组 element-wise 乘法即可。形式上看起来是类似乘性绝对位置编码的做法。

另外，看 LLAMA 中的实现，可以看到旋转位置编码是在每一个 decoder 层的输入都加了的。每次都强化一次位置信息，也有助于模型更好识别不同距离的内容。

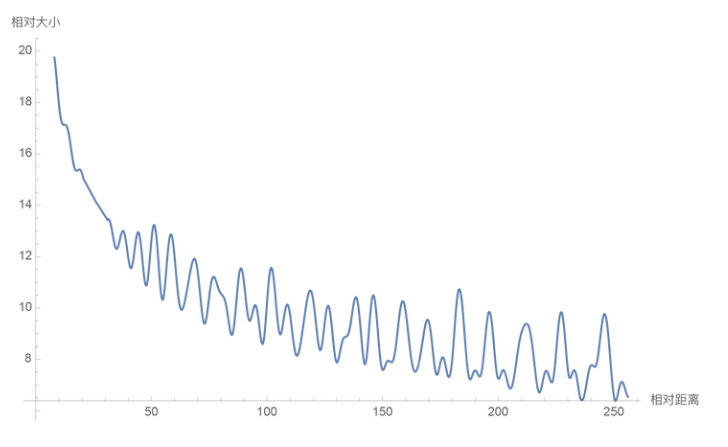
（6）远程衰减的特性

至此，旋转位置编码已经完备，具备了计算高效，实现容易，便于外推，适用于线性注意力的特性。实际上它还具备另一项优点：有远程衰减的特性。

直观看起来远程衰减很符合直觉，毕竟注意力机制随着距离的衰减而降低，这个机制和人类也很像。

4、小结

总之，RoPE 在设计和实现上还是挺巧妙的，性质上也很有很多优势，所以被广泛应用到 transformer 模型中去了。

最后的最后

感谢你们的阅读和喜欢，我收藏了很多技术干货，可以共享给喜欢我文章的朋友们，如果你肯花时间沉下心去学习，它们一定能帮到你。

因为这个行业不同于其他行业，知识体系实在是过于庞大，知识更新也非常快。作为一个普通人，无法全部学完，所以我们在提升技术的时候，首先需要明确一个目标，然后制定好完整的计划，同时找到好的学习方法，这样才能更快的提升自己。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】

大模型知识脑图

为了成为更好的 AI大模型 开发者，这里为大家提供了总的路线图。它的用处就在于，你可以按照上面的知识点去找对应的学习资源，保证自己学得较为全面。

经典书籍阅读

阅读AI大模型经典书籍可以帮助读者提高技术水平，开拓视野，掌握核心技术，提高解决问题的能力，同时也可以借鉴他人的经验。对于想要深入学习AI大模型开发的读者来说，阅读经典书籍是非常有必要的。

实战案例

光学理论是没用的，要学会跟着一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

面试资料

我们学习AI大模型必然是想找到高薪的工作，下面这些面试题都是总结当前最新、最热、最高频的面试题，并且每道题都有详细的答案，面试前刷完这套面试题资料，小小offer，不在话下

640套AI大模型报告合集

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】