机器为什么能够学习？

本系列是台湾大学资讯工程系林軒田（Hsuan-Tien Lin）教授开设的《 机器学习基石》课程的梳理。重在梳理，而非详细的笔记，因此可能会略去一些细节。

该课程共16讲，分为4个部分：

1. 机器什么时候能够学习？（When Can Machines Learn？）
2. 机器为什么能够学习？（Why Can Machines Learn？）
3. 机器怎样学习？（How Can Machines Learn？）
4. 机器怎样可以学得更好？（How Can Machines Learn Better？）

本文是第2部分，对应原课程中的4-8讲。

本部分的主要内容：

• 用案例引出学习可行性的疑问；
• 详细介绍VC维理论，它给出了机器学习的可靠性保证；
• 介绍误差的度量，以及对误差权重不同的情况的处理方法。

1 学习可行性的疑问

先来一个小学奥数题/公务员考试题：

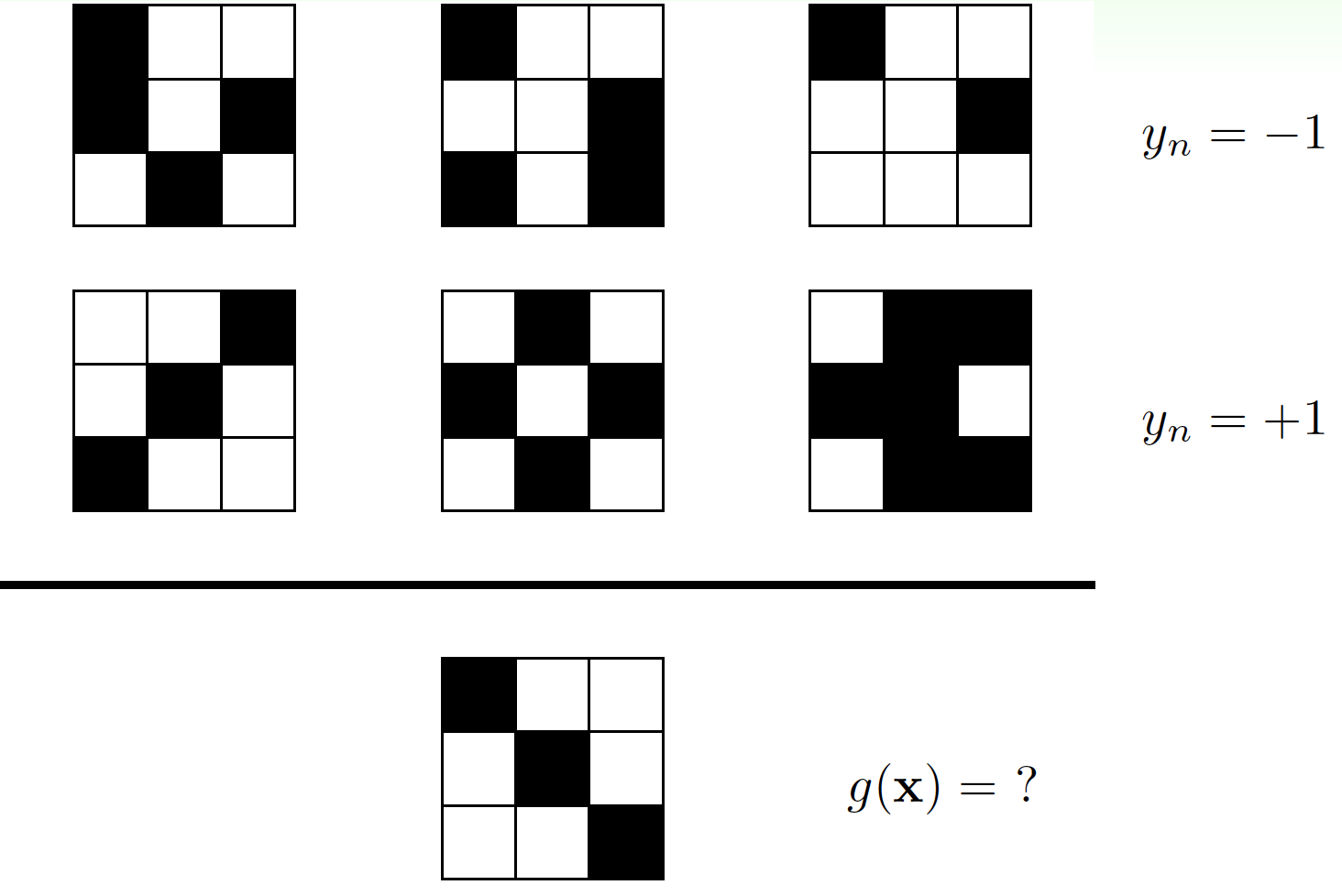
其实这个题没有标准答案，以下两种解答都是对的：

• 对称为$+1$，非对称为$-1$，因此答案是$+1$；
• 最左上角的格子白色为$+1$，黑色为$-1$，因此答案是$-1$；

因此，选择不同的规则，你会获得不同的答案。那么，如果给你一些历史数据，机器学习出某种规则，是否也会遇到这样的情况呢？

2 机器学习的可靠性保证

2.1 Hoeffding不等式

来看另一个问题：有一个罐子，里面装有许许多多黄色和绿色的小球，该如何估计黄球的比例？

很简单，抽样就行了。抽出一部分样本，计算得到样本中的黄球比例$\nu$，用这个比例作为罐子中的黄球比例$\mu$的估计即可。这样的估计准不准呢？在统计学中，有Hoeffding不等式给出准确率的界限：

$$\mathbb{P}[|\nu -\mu |>ϵ]\le 2\exp (-2{ϵ}^{2}N)$$

其中$N$为抽样的样本个数。这个式子的意思是，$\nu$和$\mu$相差较远的概率会有一个上限，在大样本下，这个上限会比较小，因此$\nu =\mu$可以叫做概率近似正确（PAC，probably approximately correct）。

2.2 机器学习中的Hoeffding不等式

现在将这个过程类比到机器学习中。罐子中的小球对应于$\mathcal{X}$中的单个数据$\mathbf{x}$，给定假设集中的一个假设$h$，罐子中黄球的比例就对应于$\mathcal{X}$中使得$h(\mathbf{x})=f(\mathbf{x})$的$\mathbf{x}$的比例。现在抽取出一部分样本，这个样本对应于现有的数据集$\mathcal{D}$，我们可以很容易地知道对$\mathcal{D}$中每一个数据$({\mathbf{x}}_n,y_n)$是否有$h({\mathbf{x}}_n)=y_n$，若相等，对应的小球为黄色，反之为绿色。我们的目的，是要知道在整个$\mathcal{X}$中满足$h(\mathbf{x})=f(\mathbf{x})$的$\mathbf{x}$的比例有多少。

若$N$足够大，且${\mathbf{x}}_n$为i.i.d.，对于某个固定的$h$来说，就可以用已知的$E_{\text{in}}(h)=\frac{1}{N}\sum _{n=1}^N{1}_{[h({\mathbf{x}}_n)\ne y_n]}$去推断$E_{\text{out}}(h)=\underset{\mathbf{x}\sim P}{E}{1}_{[h(\mathbf{x})\ne f(\mathbf{x})]}$，从而判断该$h$的表现如何，如下图：

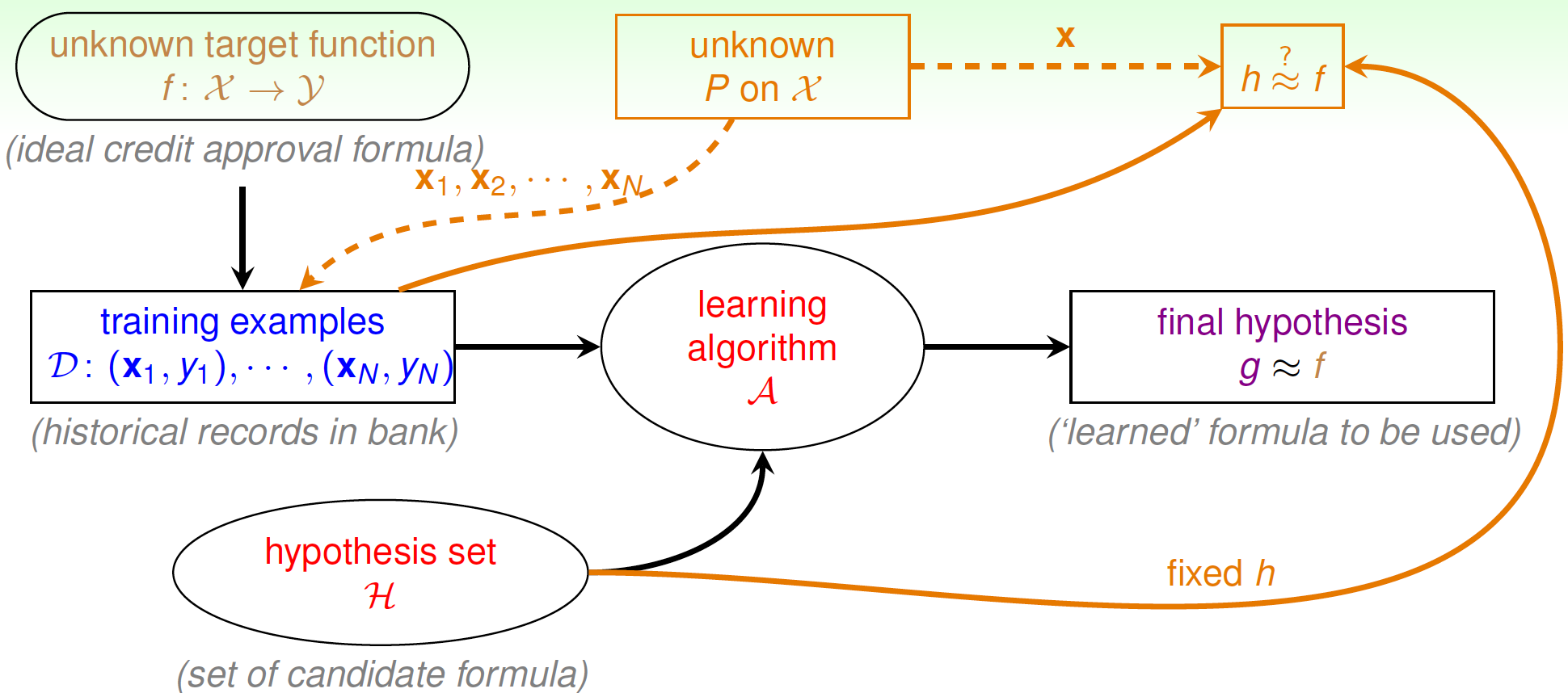
根据Hoeffding不等式，就是

$$\mathbb{P}[|E_{\text{in}}(h)-E_{\text{out}}(h)|>ϵ]\le 2\exp (-2{ϵ}^{2}N)$$

如果$E_{\text{in}}(h)$和$E_{\text{out}}(h)$足够接近，并且$E_{\text{in}}(h)$足够小，这就能保证$E_{\text{out}}(h)$足够小，也就能判断出对于抽样过程$P$，有$h\approx f$。

但是，这只能用来判断某个$h$是否足够好。如果现在是用算法$\mathcal{A}$从假设集$\mathcal{H}$中选出一个$h$，再套用上面的不等式，就会有问题。试想一下，假设有150个人，每人丢5次硬币，就有超过99%的概率会出现有某个丢5次硬币都是正面的人，这能说明他的丢硬币技术比其他人高吗？如果选择他作为我们的“$g$”，能保证他以后再去丢硬币，得到正面的概率也比其他人更大吗？

同理，如果是从$\mathcal{H}$中选出一个在样本$\mathcal{D}$内误差最小的