高斯混合模型(GMM)和EM算法【Python】

在GMM中使用EM算法

一、高斯混合模型（GMM）
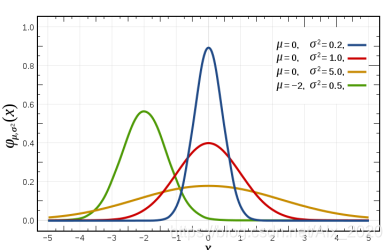
1、一维高斯分布

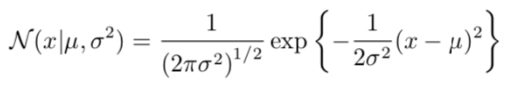
2、多维高斯分布

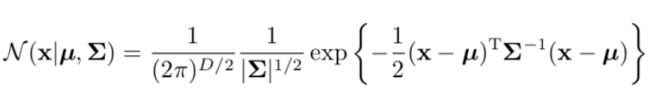
3、高斯混合模型
从几何角度来看：多个高斯分布叠加而成

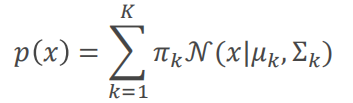
πk是x点属于哪个高斯分布的权重

二、EM算法：是一种迭代方法
E-step：更新后验概率

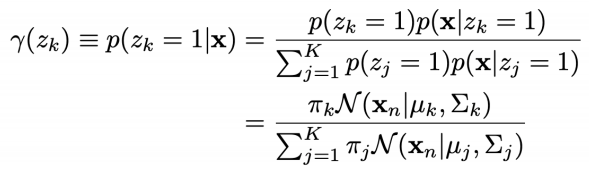
	def get_expectation(self, data):
        """
        更新posteriori(后验概率）
        :param data: 输入的数据点
        :return: 更新后的后验概率
        """
        for k in range(self.K):
            # 计算高斯分布
            self.posteriori[k] = multivariate_normal.pdf(
                data,
                mean = self.mu[k],
                cov = self.cov[k]
            )
        # ravel(): 将多维数组转化为一维数组,  np.diag(): 将一维矩阵转化为对角矩阵
        self.posteriori = np.dot(np.diag(self.priori.ravel()), self.posteriori)
        self.posteriori /= np.sum(self.posteriori, axis=0)

M-step：更新均值、协方差、先验概率
1.先求出Nk

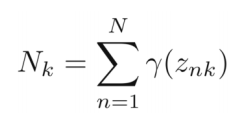
# get effective count 获得Nk的值
effecitve_count = np.sum(self.posteriori, axis=1)

2.更新GMM中的参数

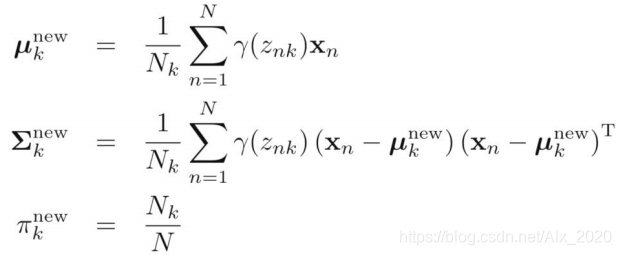
# M-step: 更新GMM的参数
self.mu = np.asarray([np.dot(self.posteriori[k], data) / effecitve_count[k] for k in range(self.K)])
self.cov = np.asarray([np.dot((data - self.mu[k]).T, np.dot(np.diag(self.posteriori[k].ravel()), data - self.mu[k]))/ effecitve_count[k] for k in range(self.K)])
self.priori = (effecitve_count / N).reshape((self.K, 1))

三、完整的代码

import numpy as np
import pandas as pd
from numpy import *
import pylab
import random