硬核推导与深度讲解：梯度消失与爆炸

第一部分： 信息的传递与失真

我们可以从一个生活中的例子开始：

想象一下，我们在玩一个“传话游戏”。第一个人（输入层）得到一个信息，然后悄悄告诉第二个人，第二个人再传给第三个人……一直传到最后一个人（输出层）。

理想情况： 信息准确无误地传递到最后。

可能出现的问题1： 如果每个人在传话时都比上一个人说得更小声、更含糊（比如只说了重点的80%），那么传到最后，信息可能就变得微弱到听不见了。这就是梯度消失。

可能出现的问题2： 如果每个人都添油加醋，把听到的信息夸大一点点，那传到最后，信息可能就变成了一个完全失实的的信息。这就是梯度爆炸。

在神经网络中，梯度是模型学习和更新的依据。这个“传话游戏”的过程就是 反向传播 (Backpropagation)。如果梯度在反向传播的过程中变得越来越小或越来越大，模型就无法有效学习。

第二部分：梯度消失与梯度爆炸

2.1 什么是梯度？

简单回顾一下：梯度是损失函数对模型参数（权重 w 和偏置 b）的导数∂J∂w。它指明了为了让损失变小，参数应该调整的方向和幅度。梯度越大，更新幅度越大；梯度越小，更新幅度越小。

2.2 梯度消失 (Gradient Vanishing)

1. 直观理解： 在深层网络中（层数很多），当梯度从输出层反向传播到靠近输入层的网络层时，梯度值变得越来越小，几乎接近于0。这导致靠近输入层的参数几乎无法得到更新，模型学习极其缓慢甚至停滞。就像传话游戏中，最开始的几个人根本不知道最后的结果是好是坏，也就无法调整自己的传话方式。

2. 数学推导： 让我们来看一个简单的深度神经网络，假设每一层都使用 Sigmoid 激活函数。

为了让推导更清晰，我先借用吴恩达老师课程中的两张图，让我们回顾一下神经网络参数传递：

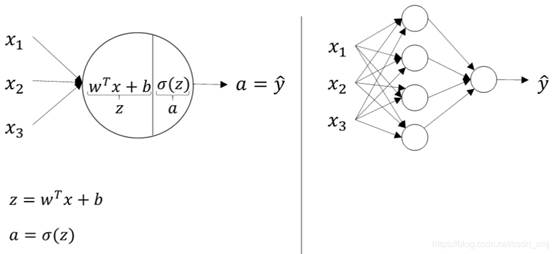
ai​: 第 i 层的激活输出。这是第 i 层神经元计算后的输出值。a0​ 就是网络的输入。

zi​: 第 i 层的线性输出。这是激活函数被应用 之前 的值。它由前一层的输出 ai−1​、权重 wi​ 和偏置 bi​ 计算得出：zi​=wi​⋅ai−1​+bi​。

σ: 激活函数，这里我们以 Sigmoid 函数为例。

关系： ai​ 是 zi​ 经过激活函数处理后的结果，即 ai​=σ(zi​)。

于是我们可以开始推导，根据链式法则，计算损失函数 J 对某一层权重 w1​ 的梯度时，需要将路径上的所有梯度相乘：

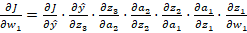
我们来看其中一个关键的环节 ，看看梯度是如何从第 i 层传递到第 i-1 层的。根据我们刚才的定义，我们可以把这个环节拆解得更细：

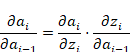
: 这一项是激活函数对它的输入求导。因为 ，所以 。

: 这一项是线性输出对前一层的激活输出求导。因为 ，所以 。

将这两部分合起来，我们就得到了梯度在两层之间传递的核心公式：

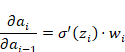
所以，整个反向传播的梯度连乘就变成了：

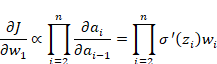
关键问题来了： Sigmoid 函数的导数  的值最大只有 0.25。

如果我们初始化的权重wi的绝对值也小于1 (通常是这样),那么多个小于1的数(例如0.25×0.5=0.125连续相乘，结果会迅速趋近于0。

梯度其他项→0

多个小于1的数相乘，随着网络层数的加深，这个连乘项会变得极小，导致整体梯度消失。

2.3 梯度爆炸 (Gradient Exploding)

1. 直观理解： 与梯度消失相反，梯度在反向传播过程中变得异常巨大。这会导致参数更新的步子迈得“太大”，甚至直接“飞出”了最优解区域，使得损失函数剧烈震荡，模型无法收敛，最终得到 NaN (Not a Number) 的损失值。

2. 数学推导： 原理与梯度消失类似，同样是链式法则的连乘效应。

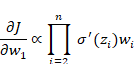
如果我们初始化的权重 wi​ 的绝对值很大（例如 > 4），即使与 Sigmoid 导数（最大0.25）相乘，其结果 σ′(zi​)wi​ 仍然可能是一个大于1的数。多个大于1的数连续相乘，结果会呈指数级增长，最终形成梯度爆炸。虽然在使用 Sigmoid 或 Tanh 时不常见，但在循环神经网络（RNN）中，由于权重在时间步上重复使用，梯度爆炸是一个更常见的问题。

第三部分：解决方法

我们该如何解决这两个“魔咒”呢？

3.1 解决梯度消失的策略

更换激活函数：ReLU

ReLU (Rectified Linear Unit) 函数，其表达式为 f(x)=max(0,x)。当输入 x>0 时，ReLU 的导数恒为 1。这意味着在连乘过程中，梯度值不会因为激活函数的导数而衰减，能够保持其原始大小，有效缓解了梯度消失问题。

残差网络 (ResNet)

引入“快捷连接”（Shortcut Connection），允许梯度直接“跳过”某些层，走一条捷径反向传播。假设某层的输出是 H(x)，改成H(x)=F(x)+x。在反向传播时，根据加法法则，来自更深层的梯度 ∂H(x)∂J​ 可以无衰减地直接传递给 x（因为 ∂x∂H(x)​=1），保证了梯度至少能以原始大小的一部分传递回去。

批标准化 (Batch Normalization)

在网络层之间，对每一批（Batch）的数据进行标准化处理，使其均值为0，方差为1。BN能够将每一层激活函数的输入值拉回到一个比较敏感的区域（例如，对于Sigmoid，是接近0的区域），在这个区域里梯度较大，从而避免梯度过小。同时，它也使得权重初始化不那么敏感，间接缓解了梯度消失和爆炸。

3.2 解决梯度爆炸的策略

1. 梯度裁剪 (Gradient Clipping) ：这是最直接也最有效的方法。在更新参数之前，检查梯度的范数（可以理解为梯度向量的长度）。如果范数超过了一个预设的阈值 (threshold)，就按比例缩小它，使其范数等于该阈值。就像给汽车设置了最高限速，不管油门踩多猛（梯度多大），速度（更新幅度）都不会超过这个限制。这样可以防止因梯度过大而导致的参数剧烈震荡。

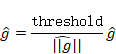
这里的 g 是所有参数的梯度组成的向量。

权重正则化 (Weight Regularization)：在损失函数中加入一个惩罚项（如 L1 或 L2 ）来限制权重的大小。 L2 正则化的目标是让权重  的值变得更小。既然梯度爆炸是因为权重过大引起的，那么通过正则化从根源上限制权重的大小，自然就能有效防止梯度爆炸。

总结：

问题	核心原因	主要后果	核心解决方案
梯度消失	深层网络的链式法则 + Sigmoid/Tanh导数小于1	模型训练缓慢，浅层网络无法学习	ReLU、ResNet、Batch Norm
梯度爆炸	深层网络的链式法则 + 权重过大	模型无法收敛，损失函数震荡/NaN	梯度裁剪、权重正则化