论文下载地址:https://arxiv.org/pdf/2409.12122
大家2026新年好,时间真快啊,一下又过去了一年,AI的发展也是日新月异,但是大概方向没有什么变化,主要还是从90-100分的精进,没有什么真正意义上的0-1革命,所以我们今天来看一下阿里千问的技术报告,学习一下另外的顶级团队,通过什么方法细节,来训练出优秀的模型。
作为新年的第一篇博客,我决定要写的非常详细,层层递进,给今年开个好头,希望今天内能写完吧。
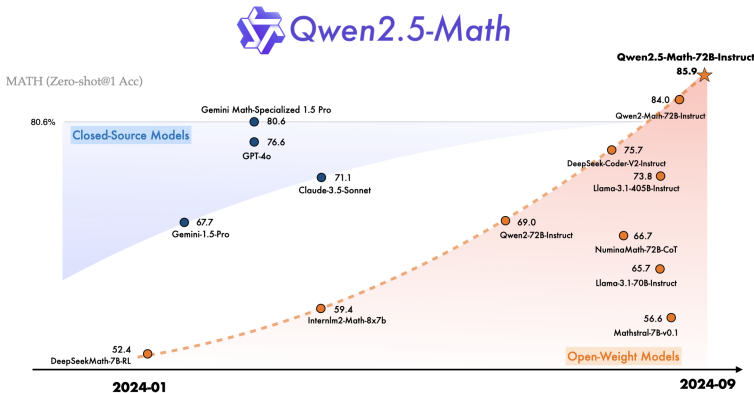
这份技术报告详细介绍了 Qwen2.5-Math 系列模型的诞生过程。这是一篇非常精彩的论文,它核心展示了如何通过自我进化的机制,让一个大模型在特定领域(数学)达到乃至超越顶尖闭源模型(如 GPT-4o)的水平。
引言与核心创新
论文首先指出,尽管大语言模型在通用任务上表现优异,但数学推理仍是挑战。Qwen2.5-Math旨在通过自我改进技术解决这一问题,其核心创新包括:
-
预训练阶段:利用前代模型Qwen2-Math-Instruct生成大规模高质量数学数据,构建Qwen Math Corpus v2(超过1万亿token),比v1版本(7000亿token)更大。
-
后训练阶段:通过奖励模型(RM)迭代优化监督微调(SFT)数据,并应用强化学习(如GRPO)进一步微调模型。
-
推理阶段:使用奖励模型引导采样,提升模型输出质量。
这些改进使得Qwen2.5-Math在数学推理上显著超越前代和当前开源模型,甚至在某些基准上超过闭源模型如GPT-4o。
预训练(Pre-training)
Qwen 团队并没有简单地把网上爬下来的数学题扔进模型,而是设计了一个包含“召回-去重-过滤-合成”的数据处理流程。
开始讲解之前,我先补充一下FastText的技术原理:
FastText 是由 Facebook AI Research (FAIR) 团队(现 Meta AI)在 2016 年开源的一个文本处理库。
正如其名,“Fast”。它是一个用于高效学习词向量(Word Embeddings)和进行文本分类(Text Classification)的工具。在 BERT、GPT 等大模型出现之前,它是工业界文本分类的首选;即便在今天的大模型时代,面对海量数据清洗(如 Common Crawl 级别的处理),它依然是不可替代的,因为它比深度神经网络(DNN)快几个数量级,但精度往往相差无几。
FastText 的架构非常简单,但极其巧妙。它可以看作是 Word2Vec 中 CBOW(Continuous Bag-of-Words)模型 的一种变体。
不同于深层的 Transformer,FastText 只有三层:
输入层 (Input Layer):输入一段文本(例如一个句子或文档)。FastText 把这段文本里的词转换成向量。
隐藏层 (Hidden Layer):将文本中的所有单词的词向量取平均,得到一个代表整个文本的“文档向量”。
输出层 (Output Layer):如果是做词向量训练:预测中心词。如果是做文本分类(Qwen2.5-Math 用到的功能):输出文本属于某个类别的概率(比如“是数学内容”还是“不是数学内容”)。
子词(n-gram)嵌入:
传统模型: 每个单词是一个独立的单元。例如,“数学”这个词对应一个向量。对于生僻词或拼写错误的词(如“数学matics”),模型无法处理。
FastText: 一个单词的向量由其组成字符的n-gram向量求和得到。
例如,对于单词 “math”(设定n=3),它的子词n-grams包括:<ma, mat, ath, th>, <m, ma, at, th, h>等(<和 >表示词边界)。“math”的词向量 = vec(<ma)+ vec(mat)+ vec(ath)+ ... 的和。
层级 Softmax —— 解决“速度”问题
这是 FastText 能够处理亿级别数据的核心原因。
普通 Softmax:如果你有 1000 万个类别(或者词表大小为 1000 万),计算一次概率需要遍历这 1000 万个节点,计算量是 O(N),非常慢。
层级 Softmax:FastText 使用霍夫曼树来组织类别。高频词/类别放在树的顶部,低频词放在底部。预测时,不需要遍历所有类别,只需要沿着树路径走下来,复杂度降低到 O(log N)。效果:这使得它在标准多核 CPU 上,几分钟内就能训练数十亿词的模型。
预训练阶段的详细技术原理和实施细节:
训练数据构建:
要解决的问题:普通的通用大语言模型(训练数据包罗万象)在需要逻辑推导和计算的数学问题上表现不佳,其根本原因之一是它们“学习”的资料中,数学相关的精华内容太少了。
解决方案:为此,研发团队决定专门打造一个聚焦数学领域的巨型语料库,为模型“补课”。
这个语料库有两个版本,规模逐步升级:
Qwen Math Corpus v1:包含约7000亿个基本语言单元(token),用于训练第一代数学增强模型 Qwen2-Math。
Qwen Math Corpus v2:规模更大,包含超过1万亿个token,用于训练更强的新一代模型 Qwen2.5-Math。
构建如此庞大且专业的语料库并非简单地收集数据,而是遵循一套精密、多步骤的自动化流程,可以类比为一条高度智能的“数据生产线”。
A. 数据召回
这是整个流程的第一步,目标是从整个互联网的汪洋大海中,把那些“像数学”的内容“捞”出来。
源头:从像Common Crawl这样的公共网络存档中筛选,其数据量极其庞大。
关键技术手段:
训练数学直觉:
准备两类“教材”:一类是已知的高质量数学文本(种子数据),另一类是普通通用文本。用这些教材“训练”一个FastText分类器。
这个分类器学会区分一段文字是“数学内容”还是“非数学内容”。
让直接越来越准:
采用迭代训练策略。先用初始分类器筛选一批数据,然后把筛选出的优质数学数据加入训练集,重新训练分类器。这个过程循环进行,每轮迭代后,分类器识别数学内容的能力都会变得更强、更精准。
顺藤摸瓜:利用已找到的数学数据的元信息(特别是URL,即网页地址),进行反向查找逻辑:如果一个网页含有数学内容,那么与其链接相关、或同一域名下的其他网页,包含数学内容的概率也更高。通过这种方法,可以发现更多在第一轮筛选中可能被遗漏的相关资料,从而扩展数据池的广度。
B. 数据去重
目的:互联网上存在大量转载、抄袭或高度相似的内容。保留所有副本是低效的,会浪费算力并可能导致模型产生偏见。
技术:使用MinHash等算法快速计算文档之间的相似度。如果两篇文档的“指纹”过于相似,则只保留一份。
C. 质量过滤
目的:去除垃圾、低质、无关或格式混乱的内容,这是提升语料库“纯度”的关键。
方法:不仅用规则(如过滤广告、过短文本),还引入了AI模型进行智能判断。
技术细节:使用一个小型的指令微调模型(Qwen2-0.5B-Instruct),通过精心设计的提示词(如“请判断以下文本作为数学训练数据的质量,从1-10打分”),让模型对数据条目进行打分,只保留高分项。这相当于用AI来为AI筛选“教材”。
D. 合成数据(核心创新)
这是整个流程的精华,体现了 “自我进化” 和 “数据驱动迭代” 的思想。
v1阶段:使用当时最强的通用指令模型(Qwen2-72B-Instruct),以两种方式创造数据:
重构与优化:从现有高质量资料(如教科书、论文)中提取知识点,并将其改写成更规范、更适合模型学习的问答对或叙述段落。
直接生成:让模型基于其知识,直接创造出新的、合理的数学问题和解答。
v2阶段(升级关键):使用在v1数据上训练出的、专门强化了数学能力的模型(Qwen2-Math-72B-Instruct) 来生成v2的合成数据。这就形成了一个良性循环:好模型 → 更好的数据 → 更好的下一代模型。
E. 数据混合
目的:单一类型的数据可能导致模型“偏科”。混合不同来源的数据(网页、书籍、代码、试题、合成数据等)能让模型获得更全面、均衡的数学能力。
科学方法:团队没有凭猜测混合,而是进行了消融实验。他们用一个小规模的模型(Qwen2-Math-1.5B)快速尝试不同的混合比例配方,观察哪种配方训练出的模型性能最好,从而为大规模训练确定“最佳食谱”。
基于上述流程,Qwen2.5-Math 相比前代实现了三重飞跃:
-
数据源质量升级:使用更强、更专业的合成模型(Qwen2-Math-72B-Instruct)来生成数据,数据质量更高。
-
数据源广度与语言升级:通过多轮召回,扩大了高质量数据来源,特别是大幅增强了中文数学数据的比重,使其中文数学能力更强。
-
基础能力升级:其训练的起点(初始化权重)是综合能力更强的Qwen2.5基座模型,而非Qwen2。这意味着它在开始学数学前,就拥有了更好的“语言理解”和“逻辑思维”基础。
去污染:确保考试公平
这是模型评估前至关重要且严谨的一步。
目的:防止训练数据中“偷看”到未来要用来评测的考题(如GSM8K、MATH数据集),否则评测分数会虚假偏高,无法反映模型真实的推理能力。
严格方法:
模糊匹配:使用13-gram匹配(连续13个字符)和最长公共子序列比率(即使文本不连续,但核心字符顺序高度相似)进行比对。
标准化处理:比对前先去除标点、空格等干扰项。
严格阈值:只要与评测集中的题目相似度超过阈值(如LCS比率>0.6),该数据就会被视为“污染数据”并坚决剔除。
实例:从互联网碎片到高质量数学语料
假设我们的目标是为模型提供关于“勾股定理”的优质学习材料。
A. 数据召回阶段:在互联网的沙漠中寻找数学绿洲
初始种子与分类器训练:
高质量数学种子:团队手头有一些公认的优质资料,例如来自维基百科、数学教科书PDF的关于勾股定理的段落。比如:“在平面几何中,勾股定理指出,直角三角形的两条直角边的平方和等于斜边的平方。即,如果a和b是直角边,c是斜边,则 a² + b² = c²。”
通用文本:从新闻、小说中随机抽取的段落。训练数学直觉:用这两类数据训练FastText分类器,让它学会区分“数学风格”和“普通风格”的文本。
在Common Crawl中“撒网捕捞”:
分类器开始扫描海量网页。它会“召回”许多包含“勾股定理”、“直角三角形”、“a²+b²=c²”等关键词的页面。但这些页面质量参差不齐:
高质量页面(我们想要的):一个教育博客,清晰解释了定理的证明和应用。
低质量页面(会被后续过滤):一个论坛帖子,只有一句话“勾股定理是啥?”,或者一个购物网站的商品标题“三角形勾股定理尺子”。
相关但非纯粹数学页面:一篇关于古希腊历史的文章,其中提到了毕达哥拉斯,但未深入数学细节。
迭代优化与元信息扩展:
迭代:第一轮召回后,我们把高质量的教育博客内容加入数学种子数据,重新训练分类器。新的分类器不仅能识别“勾股定理”这个词,还能识别“证明”、“斜边”、“平方和”等更内隐的数学语境,从而在下轮筛选中更精准。
元信息扩展:我们发现那个高质量的教育博客来自一个知名的“数学学习网”(mathlearn.com)。
行动:我们根据这个URL线索,主动去爬取该域名下的所有其他页面。
新发现:我们因此找到了同站点的“勾股定理的多种证明方法”、“勾股定理在三维空间中的推广”等深度文章。这些页面在最初的Common Crawl随机采样中可能没有被抓取到,但现在通过“顺藤摸瓜”被我们成功召回,极大地丰富了数据池的深度和广度。
B. 后续流水线处理(基于上述召回的数据)
假设我们召回了一段关于勾股定理的文本,它来自一个问答网站:
原始召回文本(低质量,需清洗):
“用户提问:怎么用勾股定理算梯子长度?
最佳答案:假设墙离地5米,梯子脚离墙3米,那梯子长就是根号下(5²+3²)=√34≈5.83米。很简单!
下面一堆评论:’谢谢!’、’楼主好人’、’我算的是5.84,四舍五入问题?’、’广告:代写数学作业请联系...’”
去重:如果全网有成千上万个完全相同的“梯子长度计算”问题,系统会只保留一份,消除冗余。
过滤:
质量过滤:系统会利用规则和模型,过滤掉无意义的短句(“谢谢!”)、广告、无关评论。
语言过滤:只保留目标语内容。
最终保留的核心内容:“用户提问:怎么用勾股定理算梯子长度?最佳答案:假设墙离地5米,梯子脚离墙3米,那梯子长就是根号下(5²+3²)=√34≈5.83米。”
合成:
为了将这段“问答”格式转化为更通用、更干净的“教材”格式,系统可能会利用模型进行重写或格式规范化。
合成后可能的高质量样本:
问题:一个5米高的墙,梯子底部距离墙根3米,请问需要多长的梯子?
解答:这构成一个直角三角形。根据勾股定理,斜边(梯子长度)c = √(a² + b²) = √(5² + 3²) = √(25 + 9) = √34 ≈ 5.83米。因此,梯子长度约为5.83米。
这个合成后的样本,结构清晰、语言规范、数学正确,是理想的训练数据。
混合优化:
最终的Qwen Math Corpus不会全是“勾股定理”。
它会将清洗、合成后的高质量应用实例(如梯子问题),与基础理论文本(如维基百科定义),以及深度扩展内容(如多种证明、三维推广),还有其他数学领域(代数、微积分、概率等)的海量优质数据,按照科学比例混合。
这样,模型在训练时就能接触到数学知识从概念定义、证明推导到实际应用的完整光谱,从而学到真正的数学推理能力,而非死记硬背。
总结流程:
原始互联网碎片 → (数据召回:从海量数据中初步筛选) → 包含噪声的初级材料 → (流水线清洗:去重、过滤、合成) → 干净、格式规范的优质样本 → (混合优化) → 与数百万其他数学主题的优质样本混合 → 最终构成Qwen Math Corpus → 用于训练出擅长数学推理的Qwen2.5-Math模型。
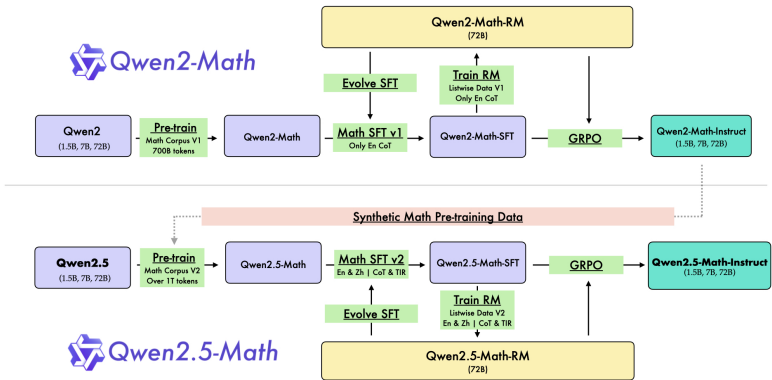
后训练(Post-training)
基于 Qwen2.5-Math 的技术报告,后训练(Post-training)阶段是提升模型数学逻辑推理能力的关键环节,核心集中在 思维链(CoT) 和 工具集成推理(TIR) 两种模式上。该阶段同样贯彻了“自我进化”的理念,主要由监督微调(SFT)和强化学习(RL)两个部分组成。
以下是后训练阶段的详细技术细节:
1. 监督微调 (Supervised Fine-Tuning, SFT)
SFT 的目标是让模型掌握两种核心能力:通过自然语言分步推理解决问题(CoT),以及利用外部工具(如 Python 解释器)解决计算或算法问题(TIR)。
我们可以把这个过程比喻为:
预训练 = 给学生(模型)一本厚重的、包罗万象的《数学百科全书》(Qwen Math Corpus),让他自学所有的概念、公式和定理。
监督微调 = 请一位高级教师,用精心准备的例题集和标准解法(SFT数据),手把手地教学生两种高级的解题技巧:1)如何写出清晰的推理步骤;2)何时以及如何使用计算工具。
核心目标:掌握两种“解题技法”
SFT的目标非常明确,就是让模型精通以下两种核心的问题解决范式:
1.思维链: 要求模型在给出最终答案前,必须用自然语言一步一步地展示其推理过程。这模仿了人类解题时的“在草稿纸上演算”的思维习惯。
价值: 这不仅提高了答案的正确率(更容易发现和纠正错误),也使模型的思考过程变得可解释、可信任。
2.工具调用: 教会模型在遇到复杂计算、符号运算或需要实时信息时,不是硬算或瞎编,而是学会调用外部工具(如Python解释器、计算器、搜索引擎等)来辅助解决。
价值: 让模型专注于其擅长的逻辑规划和语言理解,将不擅长的精确计算交给专业工具,从而极大地扩展了其解决复杂现实问题的能力。
A,思维链数据合成详解
要教会模型“思维链”,需要的不是普通的问答对,而是 <问题, 一步步的推理过程, 最终答案> 这样的高质量数据。构建这些数据本身就是一个系统工程。
第一步:问题构建
首先,需要海量、多样的数学问题作为“考题”。
规模: 约108万条问题(58万英文 + 50万中文),确保了训练的广度。
来源多元化:
现有高质量数据集: 如GSM8K、MATH。这些是公认的基准测试题,质量有保障。
合成问题: 使用如MuggleMath等方法自动生成。这能极大地扩展问题的多样性和数量,防止模型只在现有题目上过拟合。
领域增强: 特别引入了K-12(中小学)专属题库。这直接针对性地提升了模型在中文基础教育阶段数学问题上的理解和解决能力,是其中文数学能力突出的关键原因之一。
第二步:答案构建(核心技术)
有了问题,最关键的一步是生成高质量、多样化、且正确的推理步骤答案。这里采用了先进的迭代式拒绝采样策略。
流程拆解:
生成多个推理路径:
对于每一个问题,使用当前能力最强的模型(例如,在训练过程中的上一个检查点模型)生成多个(例如3-5个)不同的推理路径和答案。
这就好比让多个优秀的学生对同一道题给出不同的解法。
智能筛选最佳路径:
根据问题类型,采用不同的筛选策略:
对于有标准答案的问题:直接从生成的多个路径中,选出那些最终答案正确的路径。然后,可以从这些正确路径中随机选择一条,或选择最简洁的一条作为训练数据。
对于无标准答案的合成问题:这是技术的难点。采用 “加权多数投票”机制。
如何工作: 不只看最终答案,而是让另一个“裁判”模型(或同一模型)对所有生成的推理过程本身进行质量评估和打分。最终,选择那个被多数高质量评估所支持的、推理过程最合理、最令人信服的路径作为最佳答案。这就好比在开放性讨论中,大家投票选出逻辑最严谨、论证最充分的那个发言。
迭代优化与润色:
在Qwen2.5-Math的开发中,还利用了已经训练好的Qwen2-Math-Instruct模型来对筛选出的答案进行进一步的润色和提升,使其在语言表述、逻辑连贯性上达到更高的标准。
这就像请一位特级教师对筛选出的优秀解法进行最后批改和语言润色,使其成为完美的标准教案。
B,工具集成推理 (TIR) 数据合成
TIR 核心思想
-
痛点:让一个语言模型去计算
3.14159 * 15.7^2 / sqrt(2),它可能会给出一个看似合理但实际计算错误的数字,因为它是在“猜测”答案,而非真正计算。 -
解决方案:教会模型一种条件反射——“遇到复杂计算或算法问题,就调用专业工具(比如写一段Python代码)来搞定”。
-
类比:这就像给一位数学家配了一位精通计算、绘图、查资料的助手。数学家(模型)负责核心的逻辑规划、问题拆解和步骤设计,而具体的繁重计算和执行则交给助手(Python解释器)完成。
构建方法:在线拒绝微调
这是一种“在实践中学习,优胜劣汰” 的强化式训练方法。其核心流程是一个自我迭代提升的闭环:
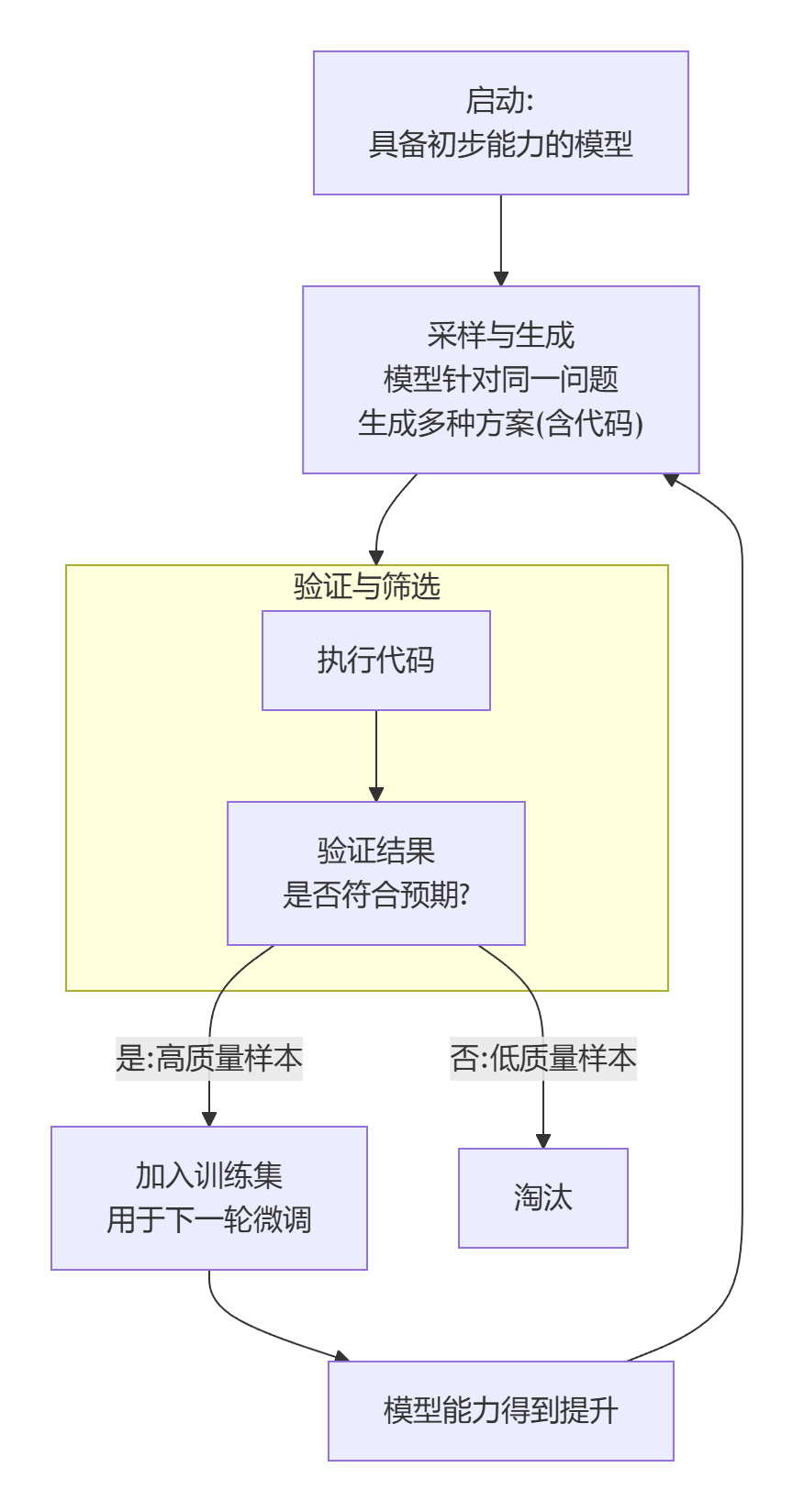
整个流程的目标,就是从模型自己尝试解决各种问题的“草稿”中,自动筛选出那些“正确使用了工具并得出正确答案”的优秀范例,然后用这些范例反过来训练模型,让它越来越擅长这件事。
实例讲解:
A,思维链数据合成:
第一步:问题构建
我们的问题库中,有这样一道题(它可能来自合成数据生成器,而不是GSM8K这类有标准答案的数据集):
问题:请证明:质数有无穷多个。
这个问题是数学上的经典定理,但证明方法不止一种,且证明过程本身是逻辑推导,没有唯一的“标准数字答案”。这正适合展示迭代式拒绝采样和加权多数投票的威力。
第二步:模型生成多个推理路径(迭代式拒绝采样)
在训练过程中,当遇到这个问题时,系统会调用当前最好的模型(假设是训练中途的 Qwen2.5-Math-7B-Instruct的某个检查点),让它为这个同一个问题生成3个不同的推理路径(即证明过程)。
模型生成的三个可能路径:
路径A(反证法 - 欧几里得经典证法):
-
假设质数只有有限个,将它们全部列出为:p₁, p₂, ..., pₙ。
-
考虑数字 N = p₁ × p₂ × ... × pₙ + 1。
-
显然,N 除以任何一个已知质数 pᵢ 都余1,所以没有 pᵢ 能整除 N。
-
那么,N 要么本身是一个新的质数(不在原列表里),要么能被一个不在原列表里的新质数整除。
-
这与“质数只有有限个”的假设矛盾。
-
结论:因此,质数有无穷多个。
路径B(反证法 - 略有不同的构造):
-
假设最大的质数是 P。
-
考虑所有质数的乘积加一:M = 2 × 3 × 5 × ... × P + 1。
-
M 大于1,且不能被任何小于等于P的质数整除。
-
根据算术基本定理,M 必然有一个质因数 q。
-
这个 q 必须大于 P。
-
这与 P 是最大质数矛盾。
-
结论:因此,不存在最大的质数,质数有无穷多个。
路径C(错误路径 - 用于示例):
-
我们知道质数序列是 2, 3, 5, 7, 11, 13...
-
可以看到,随着数字变大,质数虽然变少,但总能找到。
-
比如,在100以内有25个质数,在1000以内有168个,数量一直在增长。
-
这个增长趋势没有停止,所以质数是无穷的。
-
结论:因此,质数有无穷多个。
第三步:智能筛选最佳路径(加权多数投票)
由于这是一个“合成问题”,没有像选择题那样的标准答案,我们采用 加权多数投票 机制。这里,“投票者”可以是另一个更强大的评估模型,或者一个经过训练的“推理质量评判器”。
评估过程如下:
-
对每条路径进行质量评估打分(例如1-10分),评估维度包括:
-
逻辑严谨性:推理是否严密,有无逻辑跳跃。
-
数学正确性:每一步的数学陈述是否正确。
-
清晰度:表述是否清晰易懂。
-
简洁性:是否简洁高效。
-
-
模拟评估结果:
-
路径A:经典证法,完美无瑕。逻辑严密(标准的反证法+构造法),数学正确,表述清晰。得分:9.8
-
路径B:本质与A相同,但“假设最大质数”的出发点略显冗余,但依然完全正确。得分:9.5
-
路径C:这是一个错误证明。它使用了归纳观察(“总能找到”、“趋势在增长”)而不是逻辑证明,在数学上无效。得分:2.0
-
-
加权投票与选择:
-
系统可能会设置一个阈值(例如,只有评分>7.0的路径才参与“获胜候选”)。
-
路径C因质量太低被直接淘汰。
-
在路径A和B之间,虽然都正确,但路径A是更优美、更标准的证法,因此获得了更高的评价分数。
-
最终系统选择路径A 作为这个问题的最佳思维链答案。
-
“加权多数”体现在这里:不是简单看哪个答案出现次数多(这里每条都不一样),而是由一个更“权威”的评估体系,对答案的质量进行量化评分,最终选择质量最高的路径。这就是“质量加权”后的“多数”意见(即高质量共识)。
第四步:最终润色与入库
在Qwen2.5-Math的开发中,被选出的最佳路径(路径A)还会被送入一个更强大的、专门用于润色的模型(如Qwen2-Math-72B-Instruct)进行最后加工:
润色前(路径A原始版):
假设质数只有有限个,将它们全部列出为:p₁, p₂, ..., pₙ。考虑数字 N = p₁ × p₂ × ... × pₙ + 1。显然,N 除以任何一个已知质数 pᵢ 都余1,所以没有 pᵢ 能整除 N。那么,N 要么本身是一个新的质数,要么能被一个不在原列表里的新质数整除。这与假设矛盾。因此,质数有无穷多个。
润色后(更清晰、教学性更强的版本):
我们可以使用反证法来证明这个定理。
假设:相反地,假设质数只有有限个。不妨设这有限个质数为 p₁, p₂, …, pₙ。
构造:现在考虑一个新的自然数 N = (p₁ × p₂ × … × pₙ) + 1。
分析:显然,N 大于1。对于列表中的任何一个质数 pᵢ,当用 pᵢ 去除 N 时,得到的余数都是 1(因为 N 是所有这些质数乘积的整数倍再加1)。这意味着,列表中没有任何一个质数 pᵢ 是 N 的质因数。
推导矛盾:根据算术基本定理,任何一个大于1的自然数,要么本身是质数,要么可以写成一系列质数的乘积。既然已知的所有质数都不能整除 N,那么 N 本身就必须是一个新的质数,或者它的某个质因数是一个不在我们原有列表 {p₁, p₂, …, pₙ} 中的新质数。无论是哪种情况,我们都找到了一个不在最初列表中的质数。
结论:这与我们“质数只有这有限个”的初始假设矛盾。因此,我们的假设不成立,质数必然有无穷多个。
最终入库的SFT数据样本
经过以上所有步骤,最终生成一条用于监督微调的、高质量的思维链数据:
-
问题(Query): 请证明:质数有无穷多个。
-
回答(Response - 思维链): 【上述润色后的完整推理步骤】。
这个高质量的 <问题, 思维链答案>对,将被放入SFT数据集中,用来训练模型学会:在面对“证明质数无限”这类问题时,应该如何组织严谨、清晰的反证法逻辑进行一步步推导。
B,工具集成推理 (TIR) 数据合成
假设我们要训练模型掌握TIR能力。我们给它一个问题:
问题:一个半径为5cm的圆的面积,等于一个直角边长分别为6cm和多少cm的直角三角形的面积?
第一步:问题输入与多次采样
在ORFT训练中,系统会多次向当前版本的模型提出这个问题。每次提问时,会引入一些随机性(“温度”参数),让模型产生不同的思考路径和代码方案。
模型可能生成的几种回复方案:
方案1(优秀TIR):
# 首先计算圆的面积
import math
radius = 5
circle_area = math.pi * radius ** 2
# 设直角三角形的另一条直角边为 x,已知一条边为6
# 三角形面积 = 0.5 * 6 * x
# 令两者面积相等:0.5 * 6 * x = circle_area
x = circle_area / (0.5 * 6)
print(f“直角三角形的另一条直角边长度为: {x:.2f} cm”)最终答案:直角三角形的另一条直角边长度为: 26.18 cm
方案2(逻辑正确,代码有小瑕疵):
import math
r = 5
area = 3.1415926 * r * r # 使用了近似值,但可以接受
x = area / 3 # 正确推导了公式: area = 0.5 * 6*x => x = area/3
print(x)最终答案:26.179938779914945
方案3(纯CoT,容易出错):
“圆的面积是 π * r² = 3.14 * 25 = 78.5。三角形面积是 1/2 * 6 * a = 3a。令3a = 78.5,所以 a = 78.5 / 3 = 26.1667。所以另一条边是26.17cm。”
(这里模型在计算π25时用了近似值3.14,导致结果出现轻微偏差)*
方案4(错误使用工具):
# 模型逻辑混乱
radius = 5
side = 6
# 错误地试图用勾股定理
circle_area = 3.14 * radius * radius
other_side = (circle_area - side**2)**0.5 # 毫无逻辑的计算
print(other_side)执行结果:(78.5 - 36)^0.5 = 6.52(一个完全错误的答案)
第二步:执行代码与验证
系统会自动执行所有生成了代码的方案(方案1、2、4),并验证其最终答案是否与通过独立、可靠方法计算出的标准答案相符。
-
方案1:代码逻辑清晰,使用了
math.pi保证精度,答案正确。✅ 高质量样本,入选! -
方案2:逻辑正确,虽然用了π的近似值但结果在误差允许范围内。代码简洁。✅ 合格样本,可入选。
-
方案3:纯文本推理。虽然思路对,但计算是近似的,且没有展示使用工具的能力。❌ 这不是TIR的目标,不入选。
-
方案4:代码逻辑完全错误,答案错误。❌ 淘汰。
第三步:数据筛选与迭代训练
系统将方案1和方案2这类“正确使用工具并得到正确答案”的样本,加入“高质量TIR训练集”。然后用这个不断扩大的、经过验证的高质量数据集,对模型进行下一轮的微调。
经过多轮这样的“生成-执行-筛选-训练” 循环:
-
模型看到越来越多正确使用工具的正面例子。
-
模型逐渐学会在何时、以何种方式调用工具。
-
最终,模型在遇到计算、优化、绘图、数据处理等问题时,会优先、准确地生成代码片段来解决问题。
总结
TIR数据合成的核心价值在于:
-
扬长避短:让语言模型专注于其擅长的逻辑、规划、理解,而将不擅长的精确计算、复杂运算外包给代码解释器。
-
自我进化:在线拒绝微调 是一个高效的自我提升闭环。模型从自己的尝试中学习,通过“实践结果”这个最客观的裁判,筛选出最佳行为模式。
-
能力质变:掌握TIR的模型,其解决问题的能力范围从纯理论问题,扩展到了需要实际执行的工程计算、数据分析、算法模拟等领域,实用性大大增强。
通过 CoT(清晰的思考) 和 TIR(强大的工具) 的结合,模型最终成为一个既能“想得明白”,又能“算得准确”的智能体。
2.奖励模型训练
为了给强化学习提供比单纯“答案对错”更细粒度的反馈,团队专门训练了数学奖励模型 Qwen2.5-Math-RM 。
第一部分:核心理念——为什么需要奖励模型?
在监督微调后,模型已经学会了“如何一步步思考”和“如何使用工具”。但SFT有一个天花板:它只能模仿训练数据中的行为,无法超越数据中的最佳示例,也无法在复杂、开放的问题上进行优化选择。
想象一下教一个学生:
-
SFT阶段:是给他看标准答案和标准步骤,让他模仿。
-
奖励模型阶段:是培养一位拥有深厚功底的“裁判”。这个裁判不看标准答案(因为很多开放问题没有标准答案),而是能评判任意一个解答过程的“好坏优劣”。
为什么“答案对错”本身不够?
-
开放性问题:对于“请解释勾股定理的意义”或“设计一个节水方案”这类问题,没有唯一正确答案,但有“好坏”之分。
-
过程比结果更重要:在数学推理中,一个答案正确但逻辑跳跃、解释不清的过程,其教学价值和泛化能力,远不如一个答案正确、步骤清晰、讲解透彻的过程。我们需要奖励“优秀的思考过程”。
-
强化学习的燃料:后续的强化学习需要大量、自动化的反馈信号。我们不可能为模型生成的每一个回答都请人类标注“好”或“坏”。奖励模型就是这个自动评分器,提供细粒度的反馈信号。
所以,奖励模型的根本作用,就是将一个主观的“回答质量好坏”的问题,转化成一个可以被模型优化、可量化的“分数预测”问题。
第二部分:训练数据构建——如何制造“裁判的考卷”?
要训练一个“裁判”,首先需要一份有“标准判例”的考卷。Qwen团队是这么做的:
1. 数据规模与来源:
-
使用了总计约 61.8万 道题目(36.1万英文+25.7万中文)作为“考题”。这保证了裁判见识过足够多、足够广的题型。
-
这些题目本身来源于各种渠道,与SFT数据可能有重叠,但用途完全不同。
2. 关键:生成“回答对”并标注优劣:
-
对于每一道题目,他们用模型生成了6个不同的回答。这就像让6个不同的“考生”来解答同一道题。
-
如何标注谁好谁坏? 遵循一个基础但可靠的原则:最终答案正确的回答,优先于答案错误的回答。
-
通常,6个回答中,会有几个答案正确,几个答案错误。
-
正例:答案正确的回答。
-
负例:答案错误的回答。
-
注意:在更精细的设置中,答案正确的回答之间还可以根据步骤的清晰度进一步排序,但“答案对错”是最根本、最可靠的区分依据。
-
3. 防止“简单偏见”的巧妙设计:
-
什么是“简单偏见”? 如果所有6个回答都来自同一个“最强”的模型,那么它可能倾向于生成一些“模式化”、“取巧”的简短答案。这样训练出的奖励模型,可能会错误地认为“简短”=“好”,而惩罚那些虽然冗长但推理更严密、更富洞察力的优秀解答。
-
如何解决? 团队特意使用了不同版本、不同能力的模型来生成这些回答。这确保了“回答对”中包含了不同风格、不同难度、不同完成度的答案。
-
例如,一个较弱的模型可能生成了一个答案正确但步骤跳跃的回答。
-
一个较强的模型可能生成了一个答案正确、步骤详尽且附带解释的回答。
-
这样,奖励模型在训练时就能看到多样性,学会识别“在答案都正确的前提下,哪种解答过程更优质”,而不仅仅是识别“答案是否正确”。
-
第三部分:模型架构与训练——如何打造“裁判的大脑”?
这是技术最核心的部分。
1. 模型初始化:
-
他们没有从头训练一个新模型,而是在SFT模型的基础上进行改造。
-
SFT模型已经精通数学知识和推理步骤,是绝佳的“裁判候选人”基础。
2. 架构改造:从“生成头”到“打分头”
-
SFT模型最后有一个 “语言模型头”,它输出下一个词的概率分布,用于生成文本。
-
现在,他们把这个“生成头”替换为一个 “标量值头”。这个“打分头”非常简单,通常就是一个或几个线性层。
-
工作原理:SFT模型的主体(即前面的所有Transformer层)作为“特征提取器”,深入理解输入的整个“问题-回答”对。提取出的深层语义特征,最后传递给“打分头”。“打分头”的任务不是生成文字,而是输出一个单一的、连续的标量分数,比如 8.7 分。这个分数就代表奖励模型对这个回答质量的评估。
3. 损失函数:学习“排序”,而非“绝对值”
-
我们不要求奖励模型能准确判断一个回答是“8.5分”还是“8.6分”(绝对评分很难且主观)。
-
我们只要求它能可靠地判断两个回答中“哪一个更好”。这是一个相对简单的排序任务。
-
因此,他们使用了 “列表级排序损失函数”。这里“列表”指的是针对同一个问题的那一组(如6个)回答。
最常用的方法是Pairwise Ranking Loss(一种列表级优化思想的体现)的简化理解:
-
对于一个问题的6个回答,我们已经知道谁好(正例)谁坏(负例)。
-
损失函数会鼓励模型给正例回答打出的分数,显著高于给负例回答打出的分数。
-
公式的精髓:
Loss = -log(sigmoid(score_good - score_bad))。这个函数会惩罚“好回答分数低于坏回答分数”的情况,并让二者的分数差越大越好。 -
通过在所有“问题-回答对”上最小化这个损失,奖励模型就学会了精准排序。
-
实例演示
假设题目是:“计算 1 + 2 + 3 + ... + 100 的和。”
步骤1:构造“裁判考卷”中的一道题
-
用不同模型生成6个回答:
-
回答A(优秀): “这是一个等差数列求和问题。首项a1=1,末项an=100,项数n=100。根据公式 S = n(a1+an)/2 = 100(1+100)/2 = 5050。”
-
回答B(正确但啰嗦): “1+100=101, 2+99=101, ... 这样一共有50对,所以是101 * 50=5050。”
-
回答C(正确但跳跃): “5050。”
-
回答D(错误): “用梯形面积公式算,(1+100)*100/2=5050。哦,对了,是5050。”(逻辑错误,但答案巧合正确?这里假设我们严格判断,其推理逻辑“梯形面积公式”在此处是错误类比,因此标记为负例)
-
回答E(错误): “100 * 101/2=5050。”(无任何解释,虽然公式对,但若要求展示过程,则不合格)
-
回答F(完全错误): “5500。”
-
步骤2:标注
-
正例(答案正确且过程合理):A, B
-
负例(答案错误或过程有根本缺陷):C(无过程), D(逻辑错误), E(无过程), F(错误)
步骤3:训练奖励模型
-
模型会读取“题目”和“回答A”的全部文本,经过SFT主干网络理解后,由“打分头”输出一个分数,如
R(A) = 8.5。 -
同样得到
R(B)=7.0,R(C)=2.0,R(F)=1.0... -
损失函数会计算:
Loss = [R(C) - R(A)] + [R(F) - R(A)] + [R(C) - R(B)] + ...并希望这些差值为负(即好回答分数高),通过梯度下降调整模型参数以实现这一点。
步骤4:学成之后
-
训练完成后,这个奖励模型就可以为任何一个新的、未见过的“问题-回答对” 打出一个相对可靠的分数。
-
在后续的强化学习中,当语言模型生成一个回答,奖励模型就立刻给出分数。强化学习算法(如PPO)的目标就是调整语言模型,使其生成能获得奖励模型高分的回答。这就引导语言模型朝着“不仅答案对,而且过程优”的方向不断进化。
总结
奖励模型是一个精密的“价值观对齐器”和“质量评判官”:
-
目标:将人类对“回答质量”的复杂偏好,量化成一个可计算的分数。
-
方法:基于强大的SFT模型,将其改造成“打分器”,并用海量的、带有优劣排序标签的“回答对”数据,训练它学会精准排序。
-
关键设计:使用多模型生成回答来防止偏见,使用列表级排序损失来学习相对好坏。
-
作用:它为后续的强化学习提供了持续、自动、细粒度的优化信号,是模型实现自我超越、从“正确”走向“优秀”的核心技术组件。
3.强化学习(RL)
这是后训练的最后一步,旨在进一步优化模型的解题策略。
一、核心目标:从"正确"走向"最优"
强化学习是模型训练的最后一步,也是最关键的精炼环节。在SFT阶段,模型学会了"如何解决问题";在RM阶段,我们训练了评判回答质量的"裁判";而在RL阶段,模型要学会主动优化自己的解题策略,生成不仅正确而且质量更高的回答。
核心思想:让模型在自我尝试和反馈中学习,像人类通过练习和反思来提高一样。
二、GRPO算法详解
传统PPO的局限性
传统PPO(Proximal Policy Optimization)需要两个神经网络:
-
策略网络(Policy Network):决定采取什么行动(生成什么token)
-
价值网络(Value Network):评估当前状态的好坏
这带来了两个问题:
-
训练复杂度高,需要协调两个网络的训练
-
价值网络估计不准确会影响整个训练稳定性
GRPO的创新:去掉价值网络
GRPO(Group Relative Policy Optimization)的精妙之处在于用统计方法替代价值网络。
# 伪代码展示GRPO核心逻辑
def compute_advantages_with_grpo(responses, rewards):
"""
responses: 针对同一问题生成的多个回答列表
rewards: 每个回答对应的奖励分数
"""
# 1. 计算基线的创新方式:组内平均
baseline = mean(rewards) # 这组回答的平均奖励
# 2. 计算相对优势
advantages = []
for r in rewards:
# 优势 = 单个奖励 - 组平均奖励
advantage = r - baseline
advantages.append(advantage)
return advantages实际训练中的GRPO流程:
-
对每个问题,用当前策略生成一组回答(如8个)
-
计算每个回答的奖励
-
以这组回答的平均奖励为基线
-
优势 = 单个奖励 - 平均奖励
-
用这个优势来更新策略
为什么这样有效?
-
如果某个回答的奖励高于组平均,说明它比"平均水平"好,应该被鼓励
-
如果低于平均,说明比"平均水平"差,应该被抑制
-
这个"平均水平"是动态的、自适应的,不需要额外的价值网络来估计
三、查询筛选:寻找"学习区"
教育心理学启示
认知科学中的"最近发展区"理论:最佳的学习发生在学生"跳一跳能够到"的难度区域。
# 查询筛选的算法实现
def select_queries_for_rl(training_queries, policy_model, num_samples=8):
"""
筛选适合RL训练的问题
标准:正确回答数在2-5个之间(8次采样中)
"""
selected_queries = []
for query in training_queries:
correct_count = 0
# 对每个问题采样多个回答
for _ in range(num_samples):
response = policy_model.generate(query)
# 验证答案正确性
if verify_answer(response):
correct_count += 1
# 筛选条件:正确数在2-5之间
if 2 <= correct_count <= 5:
selected_queries.append(query)
return selected_queries为什么要这样筛选?
| 正确数范围 | 难度评价 | 是否适合RL | 原因 |
|---|---|---|---|
| 0-1个 | 太难 | 不适合 | 模型几乎不会,缺乏正面样例,学习效率低 |
| 2-5个 | 适中 | 适合 | 有成功有失败,可对比学习 |
| 6-8个 | 太简单 | 不适合 | 模型已掌握,无学习空间 |
四、奖励塑造:精细化的奖励设计
奖励公式深度解析
r = σ(α·rₘ) + (rᵥ - 1)
其中:
- rₘ: 奖励模型给出的过程质量分(通常0-1)
- rᵥ: 规则验证器的对错判断(1=正确,0=错误)
- α: 缩放因子,控制过程分的权重
- σ: sigmoid函数,将分数归一化到(0,1)奖励分步计算示例
假设有一个数学问题,模型生成了4个不同回答:
import math
def sigmoid(x):
return 1 / (1 + math.exp(-x))
# 参数设置
alpha = 3.0 # 过程分的放大系数
# 4个不同回答的情况
responses = [
# 回答1: 过程优秀,答案正确
{"r_m": 0.9, "r_v": 1, "description": "优秀且正确"},
# 回答2: 过程一般,答案正确
{"r_m": 0.6, "r_v": 1, "description": "一般但正确"},
# 回答3: 过程优秀,答案错误
{"r_m": 0.9, "r_v": 0, "description": "优秀但错误"},
# 回答4: 过程很差,答案错误
{"r_m": 0.1, "r_v": 0, "description": "差且错误"}
]
# 计算每个回答的最终奖励
for i, resp in enumerate(responses):
r_m = resp["r_m"]
r_v = resp["r_v"]
# 应用奖励公式
process_component = sigmoid(alpha * r_m) # 过程质量部分
correctness_component = r_v - 1 # 答案对错部分
total_reward = process_component + correctness_component
print(f"回答{i+1}({resp['description']}):")
print(f" 过程分 r_m={r_m:.2f} → σ({alpha}×{r_m:.2f})={process_component:.3f}")
print(f" 对错分 r_v={r_v} → r_v-1={correctness_component}")
print(f" 总奖励 = {total_reward:.3f}")
print()回答1(优秀且正确):
过程分 r_m=0.90 → σ(3×0.90)=0.965
对错分 r_v=1 → r_v-1=0
总奖励 = 0.965
回答2(一般但正确):
过程分 r_m=0.60 → σ(3×0.60)=0.858
对错分 r_v=1 → r_v-1=0
总奖励 = 0.858
回答3(优秀但错误):
过程分 r_m=0.90 → σ(3×0.90)=0.965
对错分 r_v=0 → r_v-1=-1
总奖励 = -0.035
回答4(差且错误):
过程分 r_m=0.10 → σ(3×0.10)=0.574
对错分 r_v=0 → r_v-1=-1
总奖励 = -0.426关键发现:
-
答案正确性优先:即使过程分很高(0.965),答案错误也会大幅降低总奖励
-
优秀过程有加成:在都正确的情况下,优秀过程(0.965)比一般过程(0.858)奖励高
-
惩罚机制明确:错误回答无论如何都是负奖励
五、完整RL训练流程实例
让我们通过一个具体问题来看RL的完整过程:
问题:求解方程:2x² - 5x + 3 = 0
步骤1:查询筛选
-
用当前策略生成8个回答
-
验证发现其中3个正确,5个错误
-
正确数=3 ∈ [2,5],保留这个问题
步骤2:生成回答并计算奖励
假设生成的4个代表性回答:
# 实际训练中会有8个,这里简化展示
responses_info = [
{
"response": "这是一个一元二次方程。判别式Δ=(-5)²-4×2×3=25-24=1>0,有两个实根。\n根公式:x=[5±√1]/(2×2)=[5±1]/4\n所以x₁=(5+1)/4=1.5, x₂=(5-1)/4=1",
"is_correct": True,
"process_quality": 0.95
},
{
"response": "2x²-5x+3=0\n因式分解:(2x-3)(x-1)=0\n所以x=1.5或x=1",
"is_correct": True,
"process_quality": 0.85
},
{
"response": "用求根公式:x=[5±√(25-24)]/4=[5±1]/4\n得到x=1.5和x=1",
"is_correct": True,
"process_quality": 0.70
},
{
"response": "2x²-5x+3=0\n直接观察得x=1\n代入验证:2×1-5×1+3=0,成立\n所以解是x=1",
"is_correct": False, # 漏了一个解
"process_quality": 0.60
}
]步骤3:GRPO优势计算
def calculate_rewards(responses, alpha=3.0):
rewards = []
for resp in responses:
r_m = resp["process_quality"]
r_v = 1.0 if resp["is_correct"] else 0.0
process_reward = sigmoid(alpha * r_m)
correctness_penalty = r_v - 1.0
total = process_reward + correctness_penalty
rewards.append(total)
return rewards
# 计算奖励
rewards = calculate_rewards(responses_info)
# 假设:rewards = [0.96, 0.86, 0.71, -0.33]
# GRPO优势计算
baseline = sum(rewards) / len(rewards) # 平均奖励
advantages = [r - baseline for r in rewards]
print("各回答的奖励和优势:")
for i, (resp, r, adv) in enumerate(zip(responses_info, rewards, advantages)):
print(f"回答{i+1}: {resp['response'][:30]}...")
print(f" 正确性: {resp['is_correct']}, 过程质量: {resp['process_quality']}")
print(f" 总奖励: {r:.3f}, 优势: {adv:.3f}")
print()步骤4:策略更新
根据优势值更新策略:
-
正优势:增加生成类似回答的概率
-
负优势:减少生成类似回答的概率
学习到的模式:
-
回答1(详细步骤,完全正确):优势最高 → 强烈鼓励
-
回答2(因式分解,正确):优势正 → 鼓励
-
回答3(简洁但正确):优势略正 → 适度鼓励
-
回答4(漏解,错误):优势负 → 抑制
六、训练动态与收敛
训练过程中的典型变化
训练轮次 | 平均奖励 | 正确率 | 平均过程质量
---------|----------|--------|-------------
初始 | 0.15 | 40% | 0.65
10轮后 | 0.45 | 65% | 0.78
20轮后 | 0.68 | 82% | 0.85
30轮后 | 0.82 | 90% | 0.92为什么这个设计有效?
-
自适应难度:查询筛选确保模型始终在"学习区"训练
-
相对评估:GRPO的组内比较避免了绝对值评估的主观性
-
多维度奖励:既奖励正确性,也奖励过程质量
-
自我参照:基线来自模型自身当前水平,确保"公平"比较
七、数学原理深度
GRPO的数学形式化
目标函数:
L(θ) = E[min(
ratio(θ) * A, # 优势加权
clip(ratio(θ), 1-ε, 1+ε) * A # 裁剪防止过大更新
)]
其中:
- ratio(θ) = π_θ(a|s) / π_old(a|s) # 新旧策略概率比
- A = r - baseline # 优势
- ε: 裁剪范围超参数奖励塑造的理论基础
奖励函数设计满足:
-
单调性:如果回答A在所有维度都不差于B,则r(A) ≥ r(B)
-
正确性主导:∀A,B, 如果A正确B错误,则r(A) > r(B)
-
连续性:过程质量的微小变化引起奖励的微小变化
八、总结
Qwen2.5-Math的RL训练是一个精心设计的系统工程:
-
GRPO算法:用统计方法替代价值网络,提高训练效率和稳定性
-
查询筛选:基于最近发展区理论,选择最合适的学习材料
-
奖励塑造:平衡正确性和过程质量,引导模型生成最优回答
-
迭代优化:通过多轮训练,模型策略不断精炼
这个过程让模型不仅学会了"如何解数学题",更学会了"如何更好地解数学题"——思路清晰、步骤完整、表达准确,这正是从"工具"到"助手"的质变。
4. 训练闭环
这个"闭环"描述的是Qwen2.5-Math训练中最精妙的部分——一个自我进化、自我增强的飞轮系统。
1. 跨代循环:从上一代到下一代 (The Outer Loop)
这是最大层面的闭环,连接了 Qwen2-Math 和 Qwen2.5-Math。
机制:利用上一代训练好的最强模型(Qwen2-Math-Instruct),去合成大规模、高质量的数学数据 。
作用:这些由旧模型生成的“合成数据”,被加入到新一代模型(Qwen2.5-Math)的预训练 (Pre-training) 语料库中 。
结果:新模型在“出生”时(预训练阶段),就已经学习了上一代模型的高级推理能力,从而拥有了更高的起点。
2. 训练内循环:后训练阶段的迭代 (The Inner Loop)
这是在后训练(Post-training)阶段内部进行的快速迭代,主要涉及 SFT(监督微调)模型和 RM(奖励模型)的互相促进。
步骤 A:模型生成数据 利用当前的 SFT 模型生成大量的推理样本 。
步骤 B:RM 筛选数据 使用奖励模型 (RM) 对这些样本进行打分和筛选(拒绝采样),挑出质量最高的回答 。
步骤 C:反哺 SFT 将筛选出的高质量数据作为新的训练集,去微调出一个更强的 SFT 模型 。
步骤 D:迭代更新 有了更强的 SFT 模型,又可以生成质量更高、更难的数据,进而训练出更强的 RM。更强的 RM 又能更精准地指导下一轮 SFT 数据的筛选 。
3. 最终的强化学习 (Reinforcement Learning)
在这个闭环的最后,经过多轮迭代优化的 SFT 模型和 RM 模型被结合起来:
最终 RM 提供信号,指导 SFT 模型进行 GRPO 强化学习 。
这产生了最终发布的 Instruct 模型。
闭环系统的威力:数学实例
以Qwen2.5-Math为例:
第0轮:初始构建
-
使用公开数据训练初始SFT模型
-
人工标注RM训练数据
-
训练初始RM
-
RL训练得到Qwen2-Math
第1轮闭环:
-
用Qwen2-Math生成合成数据
-
用合成数据增强预训练
-
得到更强的基座模型Qwen2.5
-
在Qwen2.5上做SFT
-
用Qwen2-Math评分筛选SFT数据
-
训练更好的RM
-
RL训练得到Qwen2.5-Math
第2轮闭环(正在进行):
-
用Qwen2.5-Math生成更高质量的合成数据
-
准备Qwen3-Math的训练...
Qwen2.5-Math的闭环训练系统代表了当前AI训练的前沿思想:
-
自我增强:模型不仅是学习目标,也是数据生成工具
-
质量筛选:用奖励模型确保数据质量不断提升
-
迭代进化:每一轮都在前一轮基础上优化
-
全面覆盖:从预训练到RL的完整闭环
这个闭环使得Qwen2.5-Math能够不断突破自身极限,在数学推理上达到顶尖水平。它不仅仅是训练一个模型,而是建立了一个能够自我进化、自我完善的AI系统。
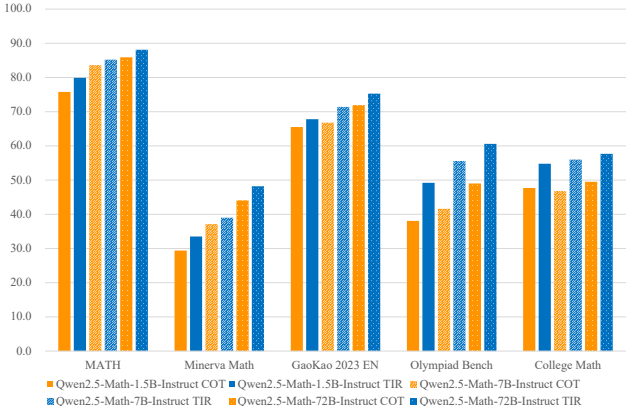
评估结果
论文在10个中英文数学基准上评估模型,包括GSM8K、MATH、GaoKao、AMC等。关键发现如下:
基础模型:Qwen2.5-Math基础模型在MATH上达到66.8分(72B),创下新SOTA。即使1.5B模型也超越多数同规模模型。
指导模型(Instruct):
CoT模式:Qwen2.5-Math-72B-Instruct在MATH上达66.8分,平均超过GPT-4o 6.2分。小模型(1.5B)性能堪比前代72B模型,显示数据改进可补偿参数规模。
TIR模式:借助Python解释器,72B模型在MATH上接近90分,1.5B模型也达80分,验证工具提升计算准确性。
中文能力:通过加入中文CoT和TIR数据,模型在中文基准(如CMATH)上提升显著,72B模型超过GPT-4o 17.5分。
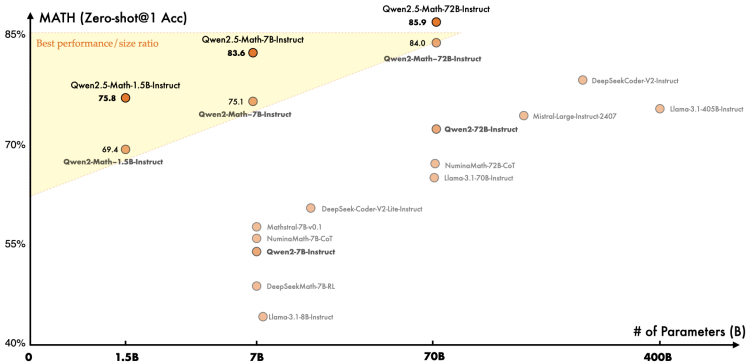
竞赛级问题:在AMC 2023和AIME 2024上,Qwen2.5-Math-72B-Instruct在TIR模式下解决几乎所有AMC问题,AIME上达12/30题,超过Claude 3 Opus等模型。





















 21
21

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








