【强化学习】强化学习数学基础：随机近似理论与随机梯度下降

Stochastic Approximation and Stochastic Gradient Descent

举个例子

首先回顾mean estimation：

• 考虑一个random variable X。
• 目标是估计$\mathbb{E}[X]$
• 假设已经有了一系列随机独立同分布的样本 { x i } i = 1 N \{x_i\}_{i=1}^N { xi​}i=1N​
• X的expection可以被估计为$$\mathbb{E}[X]\approx \bar{x}:=\frac{1}{N}\sum _{i=1}^N{x}_i$$

已经知道这个估计的基本想法是Monte Carlo estimation，以及$\bar{x}\to \mathbb{E}$，随着$N\to \infty$。这里为什么又要关注mean estimation，那是因为在强化学习中许多value被定义为means，例如state/action value。

新的问题：如何计算mean $barx$：$$\mathbb{E}[X]\approx \bar{x}:=\frac{1}{N}\sum _{i=1}^N{x}_i$$
我们有两种方式：

• 第一种方法：简单地，收集所有样本，然后计算平均值。但是该方法的缺点是如果样本是一个接一个的被收集，那么就必须等待所有样本收集完成才能计算
• 第二种方法：可以克服第一种方法的缺点，用一种incremental（增量式）和iterative（迭代式）的方式计算average。

具体地，假设$$w_{k+1}=\frac{1}{k}\sum _{i=1}^k{x}_i,k=1,2,...$$然后有$$w_k=\frac{1}{k-1}\sum _{i=1}^{k-1}{x}_i,k=2,3,...$$，我们要建立$w_k$和$w_{k+1}$之间的关系，用$w_k$表达$w_{k+1}$：$$w_{k+1}=\frac{1}{k}\sum _{i=1}^k{x}_i=\frac{1}{k}(\sum _{i=1}^{k-1}{x}_i+x_k)=\frac{1}{k}((k-1)w_k+x_k)=w_k-\frac{1}{k}(w_k-x_k)$$因此，获得了如下的迭代算法：$$w_{k+1}=w_k-\frac{1}{k}(w_k-x_k)$$
我们使用上面的迭代算法增量式地计算x的mean：

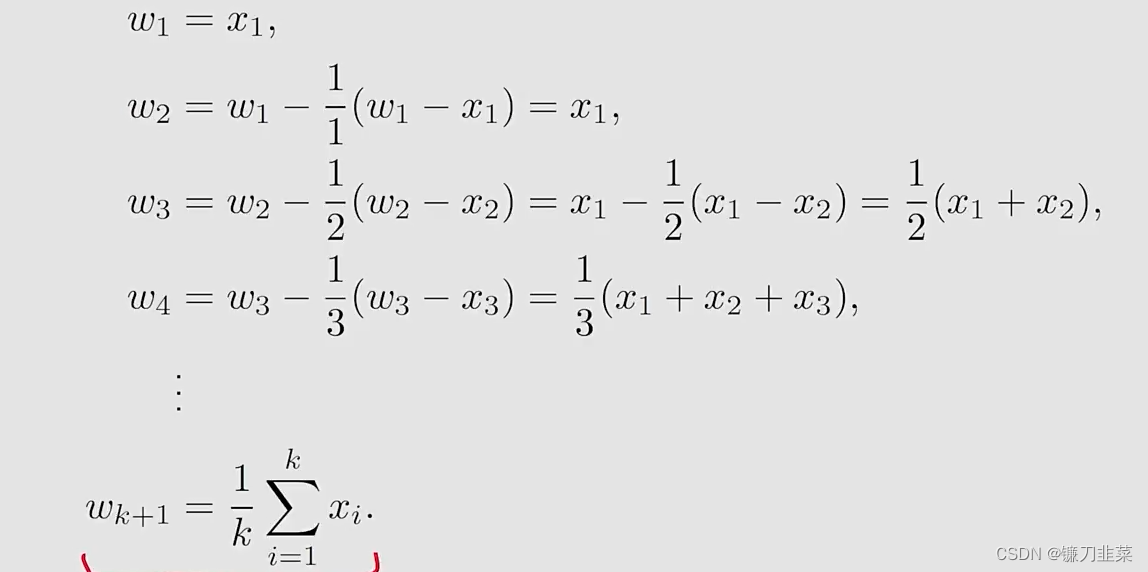
这样就得到了一个求平均数的迭代式的算法。算法的优势是在第k步的时候不需要把前面所有的$x_i$全部加起来再求平均，可以在得到一个样本的时候立即求平均。另外这个算法也代表了一种增量式的计算思想，在最开始的时候因为$k$比较小，$w_k\ne \mathbb{E}[X]$，但是随着获得样本数的增加，估计的准确度会逐渐提高，也就是$w_k\to \mathbb{E}[X]\text{ as }k\to N$。

更进一步地，将上述算法用一个更泛化的形式表示为：$$w_{k+1}=w_k-{\alpha }_k(w_k-x_k)$$，其中$1/k$被替换为${\alpha }_k>0$。

• 该算法是否会收敛到mean $\mathbb{E}[X]$？答案是Yes，如果 { α k } \{\alpha_k\} { αk​}满足某些条件的时候
• 该算法也是一种特殊的SA algorithm和stochastic gradient descent algorithm

Robbins-Monro algorithm

算法描述

Stochastic approximation (SA):

• SA代表了一大类的stochastic iterative algorithm，用来求解方程的根或者优化问题。
• 与其他求根相比，例如gradient-based method， SA的强大之处在于：它不需要知道目标函数的表达式，也不知道它的导数或者梯度表达式。

Robbins-Monro (RM) algorithm:

• This is a pioneering work in the field of stochastic approximation.
• 著名的stochastic gradient descent algorithm是RM算法的一个特殊形式。
• It can be used to analyze the mean estimation algorithms introduced in the beginning。

举个例子

问题声明：假设我们要求解下面方程的根$$g(w)=0$$，其中$w\in \mathbb{R}$是要求解的变量，$g:\mathbb{R}\to \mathbb{R}$是一个函数.

• 许多问题最终可以转换为这样的求根问题。例如，假设$J(w)$是最小化的一个目标函数，然后，优化问题被转换为$$g(w)={\nabla }_{w}J(w)=0$$
• 另外可能面临$g(w)=c$，其中$c$是一个常数，这样也可以将其转换为上述等式，通过将$g(w)-c$写为一个新的函数。

那么如何求解$g(w)=0$？

• 如果$g$的表达式或者它的导数已知，那么有许多数值方法可以求解
• 如果函数$g$的表达式是未知的？例如the function由一个artificial neural network表示

这样的问题可以使用Robbins-Monro(RM)算法求解：$$w_{k+1}=w_k-a_k\tilde{g}(w_k,{\eta }_k),k=1,2,3,...$$其中

• $w_k$是root的第k次估计
• g ~ ( w k , η k ) = g ( w k ) + η k \tilde{g}(w_k,\eta_k)=g(w_k)+\eta_k