【强化学习】强化学习数学基础：蒙特卡洛方法

将value iteration和policy iteration方法称为model-based reinforcement learning方法，这里的Monte Carlo方法称为model-free的方法。

举个例子

如何在没有模型的情况下估计某些事情？最简单的想法就是Monte Carlo estimation。

举个例子1：投掷硬币

目标是计算$\mathbb{E}[X]$。有两种方法：
Method 1: Model-based

这个方法虽然简单，但是问题是它不太可能知道precise distribution。
Method 2: Model-free
该方法的思想是将硬币投掷很多次，然后计算结果的平均数。

问题：Monte Carlo估计是精确的吗？

• 当N是非常小的时候，估计是不精确的
• 随着N的增大，估计变得越来越精确
  
  大数定理（Law of Large Numbers）：
  
  注意：样本必须是独立同分布的（iid, independent and identically distributed）

小结一下：

• Monte Carlo estimation refers to a broad class of techniques that rely on repeated random sampling to solve appriximation problems.
• Why we care about Monte Carlo estimation? Because it does not require the model!
• Why we care about mean estimation? Because state value and action value are defined as expectations of random variables！

The simplest MC-based RL algorithm

Algorithm: MC Basic
理解该算法的关键是理解how to convert the policy iteration algorithm to be model-free

Convert policy iteration to be model-free
首先，策略迭代算法在每次迭代中分为两步：

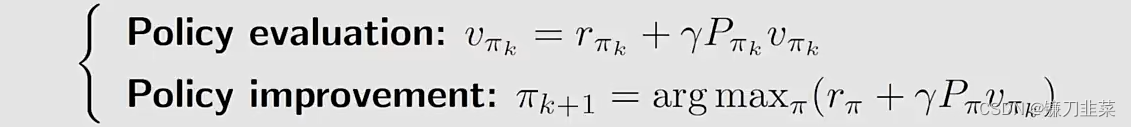
其中policy improvement step的elementwise form如下：

这里的关键是$q_{{\pi }_k}(s,a)$！计算$q_{{\pi }_k}(s,a)$有两种算法：
Expression 1 requires the model:

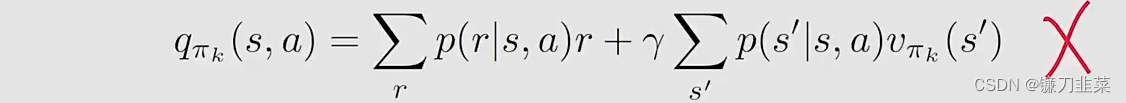
Expression 2 does not require the model：

上面的式子针对实现model-free的RL的启发是：可以使用式子2，根据数据（samples或者experiences）去计算$q_{{\pi }_k}(s,a)$。那具体是怎么做的呢？
The procedure of Monte Carlo estimation of action values：

• 首先，从一个组合$(s,a)$出发，按照一个策略${\pi }_k$，生成一个episode;
• 计算这个episode，return是$g(s,a)$
• $g(s,a)$是在下式中$G_t$的一个采样：$$q_{{\pi }_k}(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$$
• 假设我们有一组episodes和hence { g ( j ) ( s , a ) } \{g^{(j)}(s,a)\} { g(j)(s,a)}，那么$$q_{{\pi }_k}(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]\approx \frac{1}{N}$$