时序差分方法
Temporal Difference Learning
本文主要介绍temporal-difference(TD) learning,这是一个在强化学习领域比较知名的方法。Monte Carlo(MC)learning是第一种model-free方法,TD learning是第二种model-free方法。与MC方法相比,TD算法有很多优势。本文我们将研究如何将stochastic approximate methods应用于TD learning。
举个例子
首先,考虑一个简单的mean estimation问题:计算 w = E [ X ] w=\mathbb{E}[X] w=E[X]基于 X X X的一些iid采样 { x } \{x\} {
x}。
求解过程:
- 将上式重写为 g ( w ) = w − E [ X ] g(w)=w-\mathbb{E}[X] g(w)=w−E[X],我们可以将问题reformulate为一个root-finding问题 g ( w ) = 0 g(w)=0 g(w)=0
- 因为我们仅能获得 X X X中的一些采样 { x } \{x\} { x},那么观察到的噪声表示为 g ~ ( w , η ) = w − x = ( w − E [ X ] ) + ( E [ X ] − x ) ≐ g ( w ) + η \tilde{g}(w, \eta)=w-x=(w-\mathbb{E}[X])+(\mathbb{E}[X]-x)\doteq g(w)+\eta g~(w,η)=w−x=(w−E[X])+(E[X]−x)≐g(w)+η
- 根据之前的RM算法求解 g ( w ) = 0 g(w)=0 g(w)=0,即 w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − x k ) w_{k+1}=w_k-\alpha_k\tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-x_k) wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk)
然后,考虑一个稍微复杂的问题。估计一个函数 v ( X ) v(X) v(X)的mean:$ w = E [ v ( X ) ] w=\mathbb{E}[v(X)] w=E[v(X)]基于 X X X的一些iid采样 { x } \{x\} {
x}。
求解过程:
- 首先定义 g ( w ) = w − E [ v ( X ) ] g(w)=w-\mathbb{E}[v(X)] g(w)=w−E[v(X)],然后 g ~ ( w , η ) = w − v ( x ) = ( w − E [ v ( X ) ] ) + ( E [ v ( X ) ] − v ( x ) ) ≐ g ( w ) + η \tilde{g}(w, \eta)=w-v(x)=(w-\mathbb{E}[v(X)])+(\mathbb{E}[v(X)]-v(x))\doteq g(w)+\eta g~(w,η)=w−v(x)=(w−E[v(X)])+(E[v(X)]−v(x))≐g(w)+η
- 然后问题变为 g ( w ) = 0 g(w)=0 g(w)=0的求根问题,对应的RM算法是 w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − v ( x k ) ) w_{k+1}=w_k-\alpha_k\tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-v(x_k)) wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−v(xk))
再看一个例子,考虑一个更加复杂的问题。计算 w = E [ R + γ v ( X ) ] w=\mathbb{E}[R+\gamma v(X)] w=E[R+γv(X)]其中 R , X R,X R,X是随机变量, γ \gamma γ是一个常数, v ( ⋅ ) v(\cdot) v(⋅)是一个函数.
求解过程:
- 假设我们可以获得 X X X和 R R R的采样 { x } \{x\} { x}和 { r } \{r\} { r},定义 g ( w ) = w − E [ R + γ v ( X ) ] g(w)=w-\mathbb{E}[R+\gamma v(X)] g(w)=w−E[R+γv(X)],然后 g ~ ( w , η ) = w − ( r + γ v ( x ) ) = ( w − E [ R + γ v ( X ) ] ) + ( E [ R + γ v ( X ) ] − ( r + γ v ( x ) ) ) ≐ g ( w ) + η \tilde{g}(w, \eta)=w-(r+\gamma v(x))=(w-\mathbb{E}[R+\gamma v(X)])+(\mathbb{E}[R+\gamma v(X)]-(r+\gamma v(x)))\doteq g(w)+\eta g~(w,η)=w−(r+γv(x))=(w−E[R+γv(X)])+(E[R+γv(X)]−(r+γv(x)))≐g(w)+η
- 然后问题变成了 g ( w ) = 0 g(w)=0 g(w)=0的求根问题,那么对应的RM算法是 w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − ( r k + γ v ( x k ) ) ) w_{k+1}=w_k-\alpha_k\tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-(r_k+\gamma v(x_k))) wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−(rk+γv(xk)))
小结一下, 上面三个例子越来越复杂,但是都可以通过RM算法进行求解。
TD learning of state values
TD learning既可以指一大类的强化学习算法,也可以指一个具体的estimating state values的算法。TD算法是基于数据,也就是不基于模型来实现强化学习。
算法描述
TD算法要求的data/experience如下:

The TD learning algorithm如下:
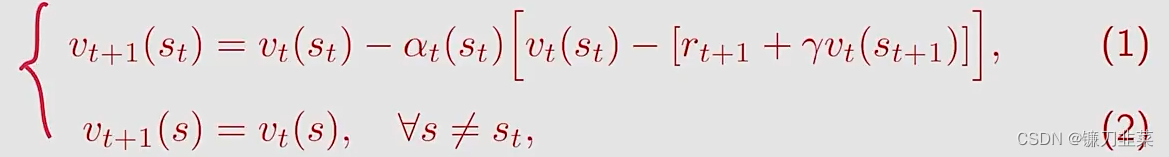
其中 t = 0 , 1 , 2 , . . . t=0,1,2,... t=0,1,2,...,这里的 v t ( s t ) v_t(s_t) vt(st)是 v π ( s t ) v_\pi (s_t) vπ(st)的estimated state value,s是state space, α t ( s t ) \alpha_t(s_t) αt(st)是在 t t t时刻 s t s_t st的学习率。
- 在t时刻,只有visited state s t s_t st的值被更新,而unvisited states s ≠ s t s\ne s_t s=st的values保持不变。
- 在等式(2)中的更新过程在后面的内容中将被省略
对TD算法进行一些标注:
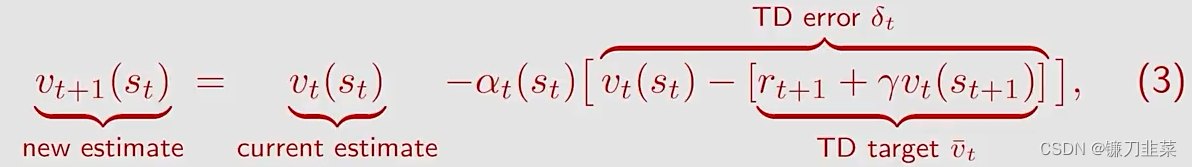
其中 v ˉ t ≐ r t + 1 + γ v ( s t + 1 ) \bar{v}_t\doteq r_{t+1}+\gamma v(s_{t+1}) vˉt≐rt+1+γv(st+1)被称为TD target。





 本文详细介绍了时序差分学习(TDlearning)在强化学习中的作用,包括状态值和动作值的估计。TDlearning是一种模型自由的学习方法,通过迭代更新来逼近贝尔曼方程。文章举例说明了TDlearning如何工作,从简单的均值估计问题到更复杂的动态环境问题。此外,还讨论了Sarsa、预期Sarsa和n步Sarsa以及Q-learning算法,这些算法都是TDlearning的变体,用于估计最优动作值。Q-learning是直接寻找最优策略的off-policy方法,而Sarsa则结合了当前策略的更新。最后,文章指出所有这些算法都是解决贝尔曼方程的近似算法,用于在无模型的情况下进行策略评估和改进。
本文详细介绍了时序差分学习(TDlearning)在强化学习中的作用,包括状态值和动作值的估计。TDlearning是一种模型自由的学习方法,通过迭代更新来逼近贝尔曼方程。文章举例说明了TDlearning如何工作,从简单的均值估计问题到更复杂的动态环境问题。此外,还讨论了Sarsa、预期Sarsa和n步Sarsa以及Q-learning算法,这些算法都是TDlearning的变体,用于估计最优动作值。Q-learning是直接寻找最优策略的off-policy方法,而Sarsa则结合了当前策略的更新。最后,文章指出所有这些算法都是解决贝尔曼方程的近似算法,用于在无模型的情况下进行策略评估和改进。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 942
942

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










