如何使用MATLAB代码编写，七种常见聚类算法等。

如何使用MATLAB代码编写，七种常见聚类算法等。
代码含详细注释，数据存入Excel，替换原有的“数据集”即可。

在MATLAB中实现七种常见的聚类算法，包括K-means、层次聚类（Hierarchical Clustering）、DBSCAN、Gaussian Mixture Model (GMM)、Spectral Clustering、Fuzzy C-Means (FCM)和Self-Organizing Map (SOM)，可以通过使用MATLAB自带的函数或第三方工具箱来完成。以下是每种算法的简要介绍及其对应的MATLAB代码示例。

1. K-means 聚类

% 加载数据
load fisheriris % 使用内置的数据集
X = meas;

% 设置聚类数
numClusters = 3;

% 应用K-means算法
[idx, C] = kmeans(X, numClusters);

% 绘制结果
figure;
gscatter(X(:,1), X(:,2), idx);
title('K-means 聚类');
xlabel('Sepal length');
ylabel('Sepal width');

2. 层次聚类（Hierarchical Clustering）

% 加载数据
load fisheriris
X = meas;

% 计算距离矩阵
D = pdist(X);

% 进行层次聚类
Z = linkage(D, 'ward');

% 显示树状图
figure;
dendrogram(Z);

% 切割树状图得到指定数量的簇
T = cluster(Z, 'maxclust', 3);

% 可视化结果
figure;
gscatter(X(:,1), X(:,2), T);
title('层次聚类');
xlabel('Sepal length');
ylabel('Sepal width');

3. DBSCAN

MATLAB没有直接提供DBSCAN函数，但可以通过Statistics and Machine Learning Toolbox中的DBSCANClusterer对象或使用第三方实现。

% 加载数据
load fisheriris
X = meas(:,1:2); % 为了简化演示只取前两维

% 如果有DBSCANClusterer对象可用，可以如下使用：
% db = DBSCANClusterer('Epsilon', .5, 'MinNumPoints', 5);
% labels = db.fit_predict(X);

% 或者使用第三方实现
% 需要先下载并添加DBSCAN.m文件到路径
labels = dbscan(X, .5, 5);

% 绘制结果
figure;
gscatter(X(:,1), X(:,2), labels);
title('DBSCAN 聚类');
xlabel('Sepal length');
ylabel('Sepal width');

4. Gaussian Mixture Model (GMM)

% 加载数据
load fisheriris
X = meas;

% 创建GMM模型
gmModel = fitgmdist(X, 3);

% 分配点到最近的高斯分量
idx = cluster(gmModel, X);

% 绘制结果
figure;
gscatter(X(:,1), X(:,2), idx);
title('Gaussian Mixture Model 聚类');
xlabel('Sepal length');
ylabel('Sepal width');

5. Spectral Clustering

MATLAB没有直接提供谱聚类功能，但可以通过自定义代码实现或使用第三方工具箱。

% 示例：简单的谱聚类实现（不完整）
% 需要自己构建相似度矩阵，并进行特征分解等步骤。
% 此处省略具体实现，可参考相关文献或第三方实现。

6. Fuzzy C-Means (FCM)

% 加载数据
load fisheriris
X = meas;

% 设置聚类数
options = [3; NaN; 1e-5; 1000]; % [c; m; error; maxiter]

% 应用FCM算法
[center, U, objFun] = fcm(X, options(1,:));

% 获取最佳聚类结果
[maxU, idx] = max(U);

% 绘制结果
figure;
gscatter(X(:,1), X(:,2), idx);
title('Fuzzy C-Means 聚类');
xlabel('Sepal length');
ylabel('Sepal width');

7. Self-Organizing Map (SOM)

% 加载数据
load fisheriris
X = meas;

% 定义网络结构
net = selforgmap([8 8]); % 8x8 网格

% 训练网络
net = train(net, X');

% 查看聚类结果
Y = net(X');
classes = vec2ind(Y);

% 绘制结果
figure;
gscatter(X(:,1), X(:,2), classes);
title('Self-Organizing Map 聚类');
xlabel('Sepal length');
ylabel('Sepal width');

这些示例展示了如何在MATLAB中应用不同的聚类算法。请注意，某些算法如DBSCAN和Spectral Clustering可能需要额外的工具箱或自定义实现。此外，对于实际应用，还需要根据具体情况调整参数和预处理步骤。

为了实现主成分分析（PCA）并可视化结果，我们可以使用MATLAB来完成这一任务。以下是完整的MATLAB代码示例，包括从Excel文件中导入数据、进行PCA处理以及绘制三维散点图。

MATLAB代码实现

% 加载数据集
filename = 'data.xlsx'; % 假设你的Excel文件名为'data.xlsx'
data = readtable(filename);

% 提取特征和目标变量
X = data(:, 1:end-1); % 假设最后一列是目标变量，其余列都是特征
Y = data{:, end}; % 目标变量

% 将表格数据转换为数组
X = table2array(X);
Y = table2array(Y);

% 数据归一化
[X_norm, ps] = mapstd(X'); % 对数据进行标准化处理
X_norm = X_norm';

% 进行PCA降维
[coeff, score, latent, ~, explained] = pca(X_norm);

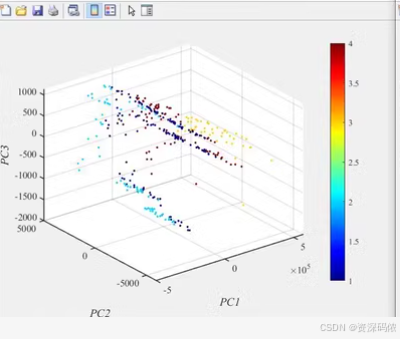
% 可视化前三个主成分
figure;
scatter3(score(:,1), score(:,2), score(:,3), 50, Y, 'filled');
xlabel('PC1');
ylabel('PC2');
zlabel('PC3');
title('PCA Visualization');
colorbar;
grid on;

% 显示解释的方差比例
disp('解释的方差比例:');
disp(explained);

% 反变换到原始空间
X_reconstructed = bsxfun(@times, score, coeff') + repmat(mean(X_norm)', size(score, 1), 1);

% 绘制重构后的数据
figure;
scatter3(X_reconstructed(:,1), X_reconstructed(:,2), X_reconstructed(:,3), 50, Y, 'filled');
xlabel('PC1');
ylabel('PC2');
zlabel('PC3');
title('Reconstructed Data Visualization');
colorbar;
grid on;

说明：

1. 加载数据：首先通过readtable函数读取Excel文件中的数据。
2. 提取特征和目标变量：假设最后一列是目标变量，其余列都是特征。
3. 数据预处理：使用mapstd函数对数据进行标准化处理。
4. PCA降维：使用pca函数进行主成分分析，并提取前三个主成分。
5. 可视化：使用scatter3函数绘制三维散点图，并使用颜色表示不同的类别。
6. 解释的方差比例：显示每个主成分解释的方差比例。
7. 反变换：将降维后的数据反变换回原始空间，并绘制重构后的数据。

示例输出：

• 三维散点图：展示PCA降维后的数据在前三主成分上的分布。
• 解释的方差比例：每个主成分解释的方差比例。
• 重构后的数据：反变换后的数据在原始空间中的分布。

希望这段代码能满足你的需求！