【剑斩OFFER】算法的暴力美学——和可被 k 整除的子数组

一、题目描述

二、算法原理

补充两个小知识：

①两个数字的余数相减一定等于0：（a - b)%k = 0   =>  a%k  - b%k = 0   => a%k = b%k

②负数取模，因为 -1 % 2  = - 1，1 % 2 = 1，这两种结果是不一样的，所以我们必须要把负数改成整数：(a % n + n)%n ，这样就能保证取模出来的数最低值为：(-(n - 1)  + n)%n = 1。这个的用法到这里是说不明白的，我们往下看就行。

---

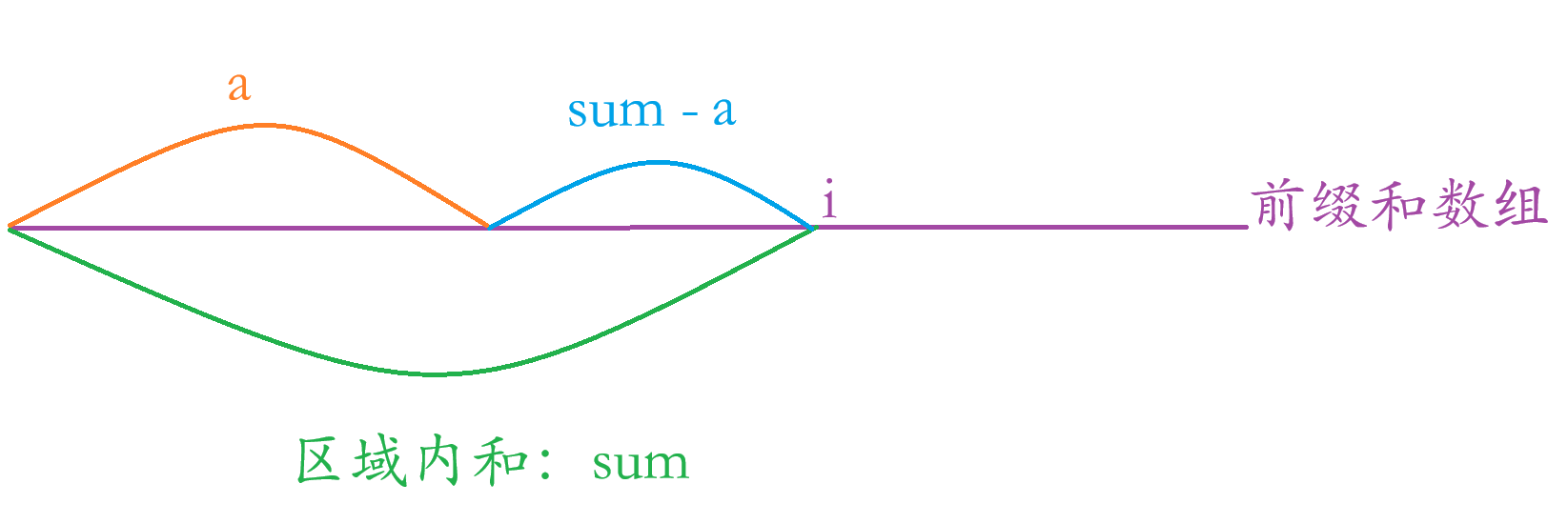
看这张图片，假设我们求数组区域内的和来到 i，到 i 点区域内的和为 sum，我们要判断 sum - a 区域的和是否 % k 是否等于 0，因为原数组的子数组有可能从下标为 0 开始到 i 这里的和%k 是不等于0，0 到 i 点内的里面的子数组是有可能是 % k 是等于0，所以sum - a 就是包含这种情况的所有集合。根据我们补充的两个知识点，所以我们可以得出 (sum - a)%k = 0 => sum%k = a%k 

所以我们只要把只要把前面求出来的前缀和%k，如果等于目前 i 点的 sum % k 的就能求出 sum  - a 模k  == 0的情况，有多少个 a % k == sum % k 就有多少个 sum - a 种情况模 k 等于0。

我们可以 a 区域内的所有的前缀和 % k 放到哈希表里面，这样可以快速遍历。

特殊情况：

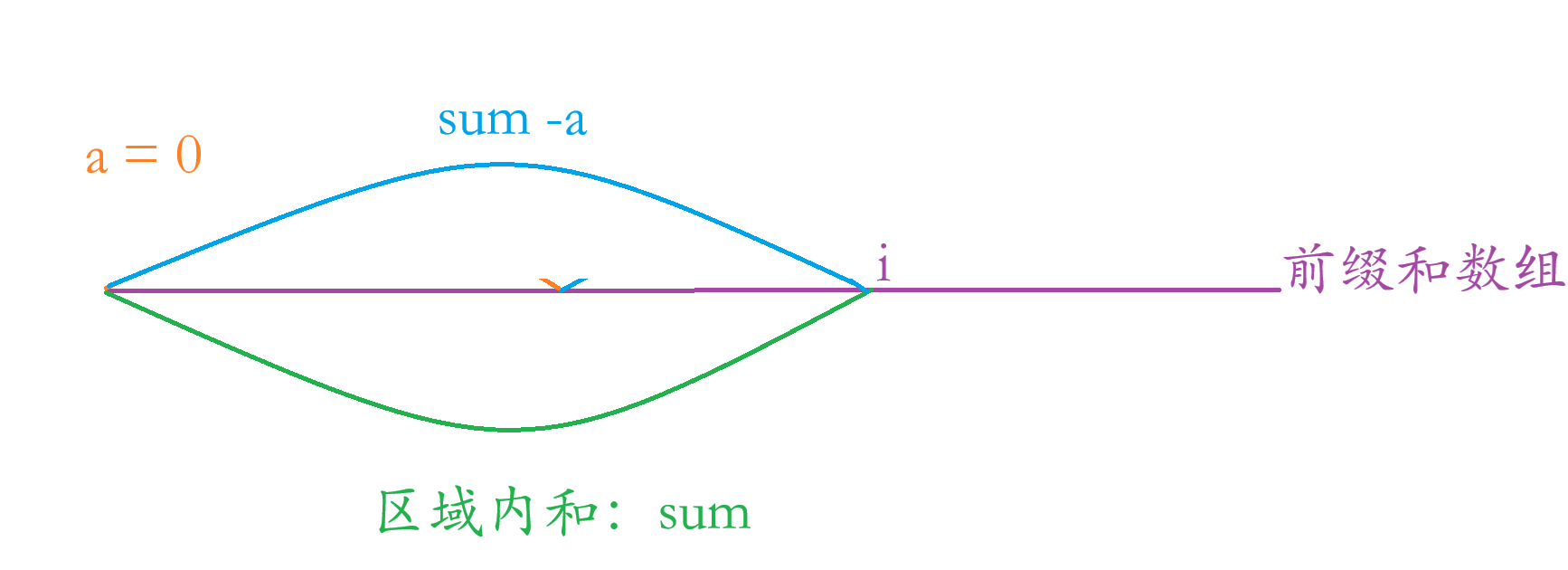
这种情况代表着原数组下标0到 i 点模上 k 等于0，导致 a = 0，此时哈希表是里面没有保存 a%k = 0，所以我们要提前放到哈希表里面。

关于 (a % n + n)%n 的运用：

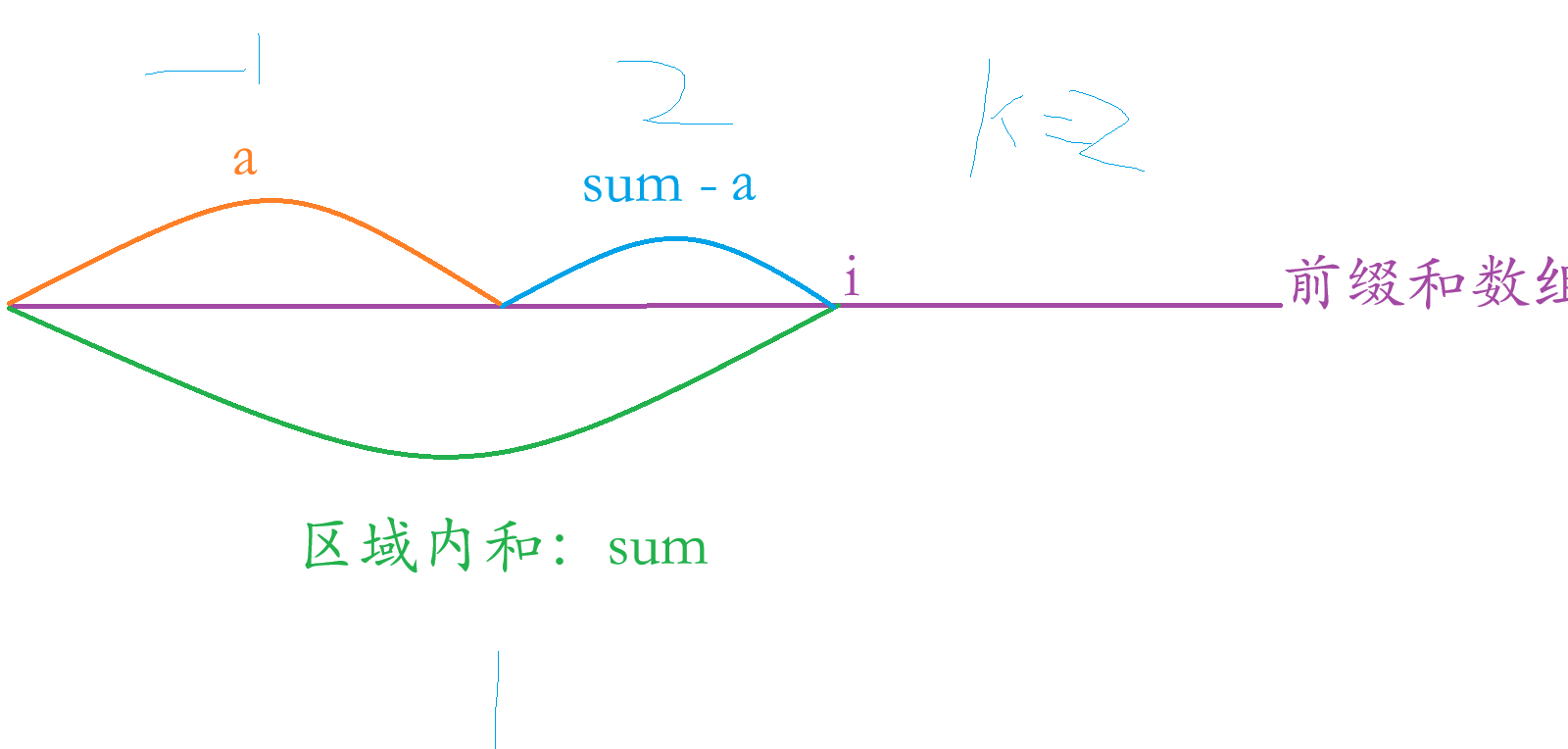
因为 sum - a = 2，2 % k = 0，是符合题目要求的，多少sum % k = 1 % 2 = 1，而且a%k =  -1 % 2 = -1，所以导致 sum % k != a%k ，不符合题目要求，这就是我们为什么要使用 (a % k + k)%k  把负数变成整数的原因。

关于 a%k 入哈希的时间，在判断有多少个 a % k == sum % k 就有多少个 sum - a 种情况模 k 等于0的情况后面，因为如果提前入哈希的话，a 就包含他了，把他归于 a 类。

三、代码实现

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        int sum = 0;
        unordered_map<int,int> hash;
        int cnt = 0;
        hash[0] = 1;
        for(int i = 0; i < nums.size(); i++)
        {
            sum += nums[i];
            if(hash.count((sum % k + k) % k)) cnt += hash[(sum % k + k) % k];
            hash[(sum % k + k) % k]++;
        }
        return cnt;
    }
};