acwing:Trie树，并查集，堆

Trie树

1.定义：高效地存储和查找字符串

例：（标记表示在此处有一个以该字母结束的英文单词）

2.例题：插入和查找字符串在集合中出现了多少次

#include <iostream>

using namespace std;

const int N = 100010;

int son[N][26], cnt[N]//表示以p结尾的单词数, idx;
char str[N];

void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';//将英文字母映射到0~25
        if (!son[p][u]) son[p][u] = ++ idx;//如果不存在则插入
        p = son[p][u];
    }
    cnt[p] ++ ;
}

int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

int main()
{
    int n;
    scanf("%d", &n);
    while (n -- )
    {
        char op[2];
        scanf("%s%s", op, str);//没有地址符号
        if (*op == 'I') insert(str);//此处表示的是值
        else printf("%d\n", query(str));
    }

    return 0;
}

并查集

1.belong[x]表示的是x属于哪个集合

2.优化：路径压缩（）

3.例题：

例题一：

#include <iostream>

using namespace std;

const int N = 100010;

int p[N];

int find(int x)返回x的祖宗节点+路径压缩
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    while (m -- )
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);//用字符串读入字符，防止scanf读入空格之类的东西
        if (*op == 'M') p[find(a)] = find(b);//合并
        else//查找是否在同一个集合
        {
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }

    return 0;
}

例题二：

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int p[N], cnt[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

此处的作用是:如果该点不是祖宗节点，则向上走一层，直到找到祖宗节点；

然后向下回溯，让每一个节点的父节点直接指向祖宗节点

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        cnt[i] = 1;
    }

    while (m -- )
    {
        string op;
        int a, b;
        cin >> op;

        if (op == "C")
        {
            cin >> a >> b;
            a = find(a), b = find(b);
            if (a != b)
            {
                p[a] = b;
                cnt[b] += cnt[a];
            }
        }
        else if (op == "Q1")
        {
            cin >> a >> b;
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
        else
        {
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }

    return 0;
}

按秩合并：将树的高度较低的插到树的高度较高的树上

堆

4.5操作在stl中无法直接实现

1.堆是一棵完全二叉树

2.小根堆：每一个点都是小于等于左右儿子的，则根节点是最小值

   大根堆则相反

3.存储：以一维数组来存，下标从1开始

     1号点是根节点，x的左儿子是2x，右儿子是2x+1

3.两个操作：up(x),down(x)

以小根堆为例，前者是某节点的值变小了需要向上移，后者是某一个点的值变大了需要向下移

4.

5.例题：

如果建立堆时，挨个往堆里插，时间复杂度是O（log n）；

此处有时间复杂度为O（n）的做法：down(n/2~1)  

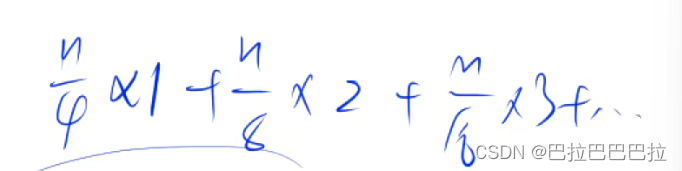
例一：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], size;

void down(int u)
{
    int t = u;//t表示最小值的下标
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;//与左儿子比较，使得t是最小值的下标
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//与右儿子比较，使得t是最小值的下标
    if (u != t)//说明根节点不是最小值
    {
        swap(h[u], h[t]);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u / 2] > h[u])
    {
        swap(h[u / 2], h[u]);
        u /= 2;
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    size= n;

    for (int i = n / 2; i; i -- ) down(i);

    while (m -- )
    {
        printf("%d ", h[1]);
        h[1] = h[size -- ];
        down(1);
    }

    puts("");

    return 0;
}

例二：

ph[k]表示第k个插入的某点在堆里面的下标是什么

hp[k]表示堆里面的某点是第几个插入的点

#include <iostream>
#include <algorithm>
#include <string.h>

using namespace std;

const int N = 100010;

int h[N], ph[N], hp[N], size;

void heap_swap(int a, int b)//修改时，既要交换值，也要交换地址
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

int main()
{
    int n, m = 0;
    scanf("%d", &n);
    while (n -- )
    {
        char op[5];
        int k, x;
        scanf("%s", op);
        if (!strcmp(op, "I"))
        {
            scanf("%d", &x);
            size ++ ;
            m ++ ;
            ph[m] = size, hp[size] = m;
            h[size] = x;
            up(size);
        }
        else if (!strcmp(op, "PM")) printf("%d\n", h[1]);
        else if (!strcmp(op, "DM"))
        {
            heap_swap(1, size);
            size-- ;
            down(1);
        }
        else if (!strcmp(op, "D"))
        {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, size);
            size -- ;
            up(k);
            down(k);
        }
        else
        {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }

    return 0;
}