acwing:单链表，双链表，邻接表，栈，队列

最新推荐文章于 2025-05-24 19:20:32 发布

巴拉巴巴巴拉

最新推荐文章于 2025-05-24 19:20:32 发布

阅读量485

点赞数 17

文章标签： c++ 算法图论

本文链接：https://blog.youkuaiyun.com/2302_79926174/article/details/138289790

版权

文章介绍了如何在C++中使用单链表和双链表进行操作，包括添加、删除节点，以及邻接表的运用。还讨论了栈、队列和单调栈的概念，以及滑动窗口问题的单调队列解决方案。最后提及了KMP算法的基本概念和应用实例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

单链表

https://www.acwing.com/activity/content/code/content/42977/

#include <iostream>

using namespace std;

const int N = 100010;

// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
head = -1;
idx = 0;
}

// 将x插到头结点
void add_to_head(int x)
{
e[idx] = x, ne[idx] = head, head = idx ++ ;
}

// 将x插到下标是k的点后面
void add(int k, int x)
{
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}

// 将下标是k的点后面的点删掉
void remove(int k)
{
ne[k] = ne[ne[k]];
}

int main()
{
int m;
cin >> m;

init();

while (m -- )
{
int k, x;
char op;

cin >> op;
if (op == 'H')
{
cin >> x;
add_to_head(x);
}
else if (op == 'D')
{
cin >> k;
if (!k) head = ne[head];
else remove(k - 1);
}
else
{
cin >> k >> x;
add(k - 1, x);
}
}

for (int i = head; i != -1; i = ne[i]) cout << e[i] << ' ';
cout << endl;

return 0;
}

双链表

邻接表

1.将每个节点相邻的边存下来

2.实质：n个单链表

栈

tt表示栈顶下标

队列

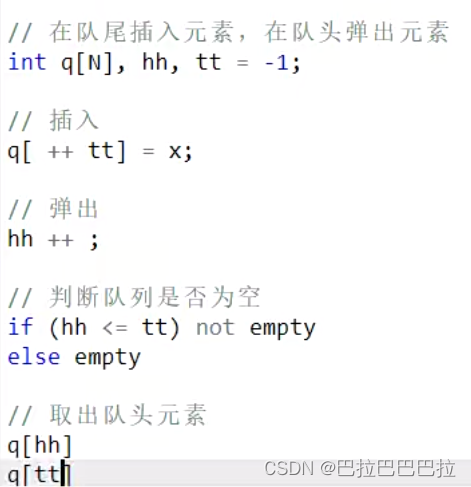
hh表示队头指针，tt表示队尾指针

单调栈

在一个数组中找到一个左（右）边离它最近（远）的数

暴力做法：把a1~an-1所有的数存在一个栈顶中，从栈顶开始找符合题意的点

本题代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 100010;

int n;
int stk[N], tt;

int main()
{
cin >> n;

   for (int i = 0; i < n; i++)
   {
       int x;
       cin >> x;
       while (tt && stk[tt] >= x)tt--;
       if (tt)cout << stk[tt] << ' ';
       else cout << "-1" << ' ';

       stk[++tt] = x;
   }
   return 0;

}

单调队列（滑动窗口）

模型：求滑动窗口中的最大值和最小值

队列当中仅存储滑动窗口里的数，每次滑动分两步进行，第一步将新的数从队尾插入，第二步将队头的数弹出

注：队列当中存的不是值，而是下标

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1000010;

int n, k;
int a[N], q[N];

int main()
{
cin >> n >> k;
for (int i = 0; i < n; i++)cin >> a[i];

   int hh = 0, tt = -1;
   for (int i = 0; i < n; i++)
   {
       if (hh <= tt && i - k + 1 > q[hh])hh++;//判断队头元素是否已经滑出窗口
       while (hh <= tt && a[q[tt]] >= a[i])tt--;
       q[++tt] = i;//因为i有可能是最小的
       if (i >= k - 1)cout << a[q[hh]]<<' ';
   }

hh = 0, tt = -1;
   for (int i = 0; i < n; i++)
   {
       if (hh <= tt && i - k + 1 > q[hh])hh++;//判断队头元素是否已经滑出窗口
       while (hh <= tt && a[q[tt]] <= a[i])tt--;
       q[++tt] = i;//因为i有可能是最小的
       if (i >= k - 1)cout << a[q[hh]]<<' ';
   }

   return 0;
}