区间DP（模板）

引入：

区间类的DP不同于线性DP，常常以区间设状态，用合并小区间的办法状态转移。

例题1：

石子合并（弱化版）

题目描述

设有 $N(N\le 300)$ 堆石子排成一排，其编号为 $1,2,3,\cdots ,N$。每堆石子有一定的质量 $m_i(m_i\le 1000)$。现在要将这 $N$ 堆石子合并成为一堆。每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同，合并的总代价也不相同。试找出一种合理的方法，使总的代价最小，并输出最小代价。

输入格式

第一行，一个整数 $N$。

第二行，$N$ 个整数 $m_i$。

输出格式

输出文件仅一个整数，也就是最小代价。

样例 #1

样例输入 #1

4
2 5 3 1

样例输出 #1

22

---

思路：

我们设 $f[i][j]$ 表示 $[i,j]$ 的最小代价。

状态转移：

我们枚举一个中间点 $k$ ，把大区间 $[i,j]$ 划分成两个小区间 $[i,k]$ 和 $[k+1,j]$ ，再合并，取最小值即可。

合并 $[i,k]$ 的代价为 $f[i][k]$。

合并 $[k+1,j]$ 的代价为 $f[k+1][j]$。

把两个小区间合并的代价其实就是整个区间的和，用前缀和加速。

得到方程： $f[i][j]=min(f[i][k]+f[k+1][j]+sum(i,j))$

结果就是 $f[1][n]$。

注意：我们是合并小区间得到的，所以要先枚举区间长度，再枚举左端点，算出右端点，再转移。

左端点为 $l$，区间长度为 $len$，求右端点 $r$:

有：$len=r-l+1$

$r-l=len-1$

$r=l+len-1$

代码：

#include <iostream>
using namespace std;
// 设 f[i][j] 表示合并 i~j 的结果

// 初始化 f[i][j] = 正无穷, f[i][i] = 0

// 状态转移：
// 可以枚举一个点 k，把区间分成 [i, k]和[k+1, j]
// 该次合并的代价为这个区间所有的石子和，用前缀和算出 
// 最后取最小值就可以了 
// f[i][j] = min(f[i][k]+f[k+1][j]+(sum[j]-sum[i-1]))

// 最后的结果就是 f[1][n]  
int n, a[305], f[305][305], sum[305];
int main()
{
	cin >> n;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			f[i][j] = 1000000000;
	for (int i=1;i<=n;i++)
	{
		cin >> a[i];
		sum[i] = sum[i-1]+a[i];
		f[i][i] = 0;
	} 
	for (int len=2;len<=n;len++) // 枚举区间的长度，先处理小区间 
	{
		for (int l=1;l+len-1<=n;l++) // 枚举左端点 
		{
			int i = l, j = l+len-1; // 计算左右端点 
			for (int k=i;k<j;k++) // 枚举中间点 k，状态转移 
			{
				f[i][j] = min(f[i][j], f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
			}
		}
	}
	cout << f[1][n]; // 输出结果 
	return 0;
} 

AC记录

---

例题2：

[NOI1995] 石子合并

题目描述

在一个圆形操场的四周摆放 $N$ 堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的 $2$ 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。

输入格式

数据的第 $1$ 行是正整数 $N$，表示有 $N$ 堆石子。

第 $2$ 行有 $N$ 个整数，第 $i$ 个整数 $a_i$ 表示第 $i$ 堆石子的个数。

输出格式

输出共 $2$ 行，第 $1$ 行为最小得分，第 $2$ 行为最大得分。

样例 #1

样例输入 #1

4
4 5 9 4

样例输出 #1

43
54

提示

$1\le N\le 100$，$0\le a_i\le 20$。

---

思路：

我们设 $f[i][j][0]$ 表示最小值， $f[i][j][1]$ 表示最大值。

方程和转移同上，只相差了 $max()$ 和 $min()$ 两个函数：

$f[i][j][0]=min(f[i][k][0]+f[k+1][j][0]+sum(i,j))$

$f[i][j][1]=max(f[i][k][1]+f[k+1][j][1]+sum(i,j))$

可以发现，这样只是多了环形的条件，我们考虑如何解决环形的问题。

例如，题中的环如下图：

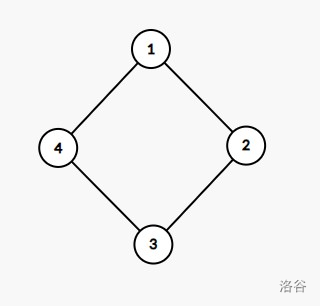
数据：

4
1 2 3 4

我们把原本的数组延长一倍，让 $a[1]=a[n+1]$,$a[2]=a[n+2]$,$a[i]=a[n+i]$

延长后的数组：1 2 3 4 1 2 3 4

该数组的下标：1 2 3 4 5 6 7 8

我们要把环拆成链：

1. 可以从 $1$ 处拆，得到 1 2 3 4，可以发现这正是延长后的数组中第 $1$ 项到第 $1+4-1=4$ 项。

2. 可以从 $2$ 处拆，得到 2 3 4 1，可以发现这正是延长后的数组中第 $2$ 项到第 $2+4-1=5$ 项。

可以发现规律：从第 $i$ 项拆开得到的序列在延长后的数组对应区间 $[i,i+n-1]$。

利用这个，我们可以对延长后的数组进行 DP，取每一个区间 $[i,i+n-1]$的最大和最小值即可。

代码：

#include <iostream>
using namespace std;
#define int long long
int f[205][205][2];
int a[205], sum[205];
// f[i][j][0] -> 最小
// f[i][j][1] -> 最大
signed main()
{
	int n;
	cin >> n;
	for (int i=1;i<=n;i++)
	{
		cin >> a[i];
		a[i+n] = a[i];
	}
	for (int i=1;i<=2*n;i++)
	{
		for (int j=1;j<=2*n;j++)
		{
			f[i][j][0] = 1000000000;
			f[i][j][1] = 0;
		}
	}
	for (int i=1;i<=2*n;i++)
		f[i][i][0] = f[i][i][1] = 0;
	for (int i=1;i<=2*n;i++)
		sum[i] = sum[i-1]+a[i];
	for (int len=2;len<=2*n;len++)
	{
		for (int i=1;i+len-1<=2*n;i++)
		{
			int l = i, r = i+len-1;
			for (int k=l;k<r;k++)
			{
				f[l][r][0] = min(f[l][r][0], f[l][k][0]+f[k+1][r][0]+(sum[r]-sum[l-1]));
				f[l][r][1] = max(f[l][r][1], f[l][k][1]+f[k+1][r][1]+(sum[r]-sum[l-1]));
			}
		}
	}
	int Max = 0, Min = 10000000000;
	for (int i=1;i+n-1<=2*n;i++)
	{
		Max = max(Max, f[i][i+n-1][1]);
		Min = min(Min, f[i][i+n-1][0]);
	}
	cout << Min << endl << Max;
	return 0;
}

AC记录