机器学习——线性回归算法、代价函数、梯度下降算法基础

线性回归

还是以之前的预测房价为例，根据不同尺寸的房子对应不同的售价组成的数据集画图，图如下

监督学习算法工作流程

假设函数其实就是我们所说的函数，在房价这个例子中，我们可以从上图中看出房价和房子面积是一个一元的线性函数（当然有更复杂更贴近数据集的函数拟合数据集，但是我们从最简单的开始学习），所以我们要来预测y关于x的线性函数，可以简单写成：y = h(x)，但它更完整的写法是下图的形式：

接下来的例子中会用到的一些符号

训练集：数据集又称为训练集，如下面的房价数据集

小写字母m：训练集中样本的数量，也就是数据集中总的数据个数

小写字母x：输入变量，这里指的是房子的面积

小写字母y：输出变量，预测的对应面积x的房子售价

(x, y)：表示某一个训练样本，如房价数据集中的某一行数据

(x^i, y^i)；i是上标，表示第i个样本

代价函数

下面介绍的代价函数称为平方误差函数，有时还称为平方误差代价函数。，是代价函数中的一种，在解决线性回归问题中比较常用，当然还有其他代价函数

模型参数介绍

如图，我们要做的是如何选择两个模型参数，以让假设函数更贴近训练集，也就是选择对两个模型参数θ0和θ1，会让预测结果更准确

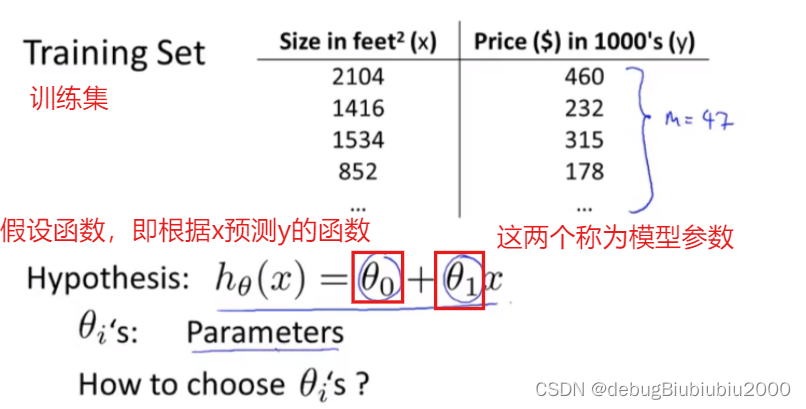
 模型参数的选择

选择不同的模型参数，会得到不同的假设函数

现在我们要根据训练集，得出两个模型参数的值，进而得到具体的假设函数，让该假设函数尽可能多的与训练集中的数据点拟合。那我们该怎么选择这两个模型参数呢？

思路是：对于训练集中的每个数据，每个房子面积x都对应着已知的售价y，假如已经确定两个模型参数，即已经得到假设函数，应该使得对该假设函数输入训练集中的某个x得到的yy，与实际的y最接近（也就是我们说的要最大程度的拟合数据点）<