西瓜书笔记（2.模型的评估与选择）（更新中）

机器学习将在训练集上的出错率成为“经验误差”，“训练误差”，而相对的，将正确率称为精度（accuracy），而将在新样本出现的错误率称为“泛化误差”，而“训练误差”接近0并不意味着模型很好，相反，这样的模型一般都具有较高的“泛化误差”，好的模型应该是从训练集中寻找规律，使其“泛化误差”最小。

”训练误差“接近0也称为“过拟合”，与其相反的是“欠拟合”，即为在训练集上经常出错。

机器学习中，欠拟合一般由模型学习力低下导致，可以通过简单的处理提高模型的学习能力，而过拟合是由于学习力过强导致的，他的解决比较困难而且无法彻底避免，他是机器学习的主要问题，任何主流算法都有专门解决过拟合的方法。附上24页插图

因为过拟合的普遍性，所以我们要通过测试集来评估模型，从而让我们由依据去选择合适的模型。

测试集行该尽可能与训练集 ∩ 空，从样本分布中独立同分布采集，尽最大可能避免从数据集来源产生的误差。

---------------------------------------------------------------------------------------------------------------------------------

训练模型时，当我们的数据集为m时，如何划分训练集和测试集？

流出法：

将数据集分为A，B两个数据集，一个用于训练，一个用于测试，两个集合的划分行该同层次相等，尽可能避免数据集成分不同导致的误差，例如训练垃圾邮件识别时，如果训练集有34%的垃圾邮件，那么测试集也要有34%的垃圾邮件

需要注意：训练集要比测试集大

交叉验证法（k折交叉验证）：

将集合分为 k 个互斥的集合，划分要保持分布一致，每次取出一个当测试集，剩下的当训练集，重复k次使所有的小集合都当过测试集，然后将k次的结果取平均值

图来自p26

留一法：

交叉验证的特殊形式

当 k =  集合元素个数时（小集合的元素数为1），留一法被公认为是最准确的方法，但是显而易见的他的耗时太大

自助法：

当数据集规模很小时，很难划分“成分相同”的数据集，所以产生了自助法，每次在数据集中抽取1个样本，然后放入训练集中，每个样本可重复抽取，经过一定次数的抽取后，有一部分进入了训练集，剩下的即为测试集

在经过m次抽取后，不被抽取的几率为：(1 - 1/m)^m，当m趋近为正无穷时，

(1 - 1/m)^m = 1/e ≈ 0.368，所以 训练集 ： 测试集 接近 2 ：1

自助法在数据集很小时好用，但当数据集足够时，还是推荐选择交叉验证和流出法

---------------------------------------------------------------------------------------------------------------------------------

在机器学习中，很多算法都有重要的参数设置，在选择合适的算法时，还要配置合适的参数，这就是调参

参数的选择一般是一个数字，在选择参数时应该选择合适的步长和范围，从而确定要训练的参数，

例如[0 - 6]步长为3，就行该选择[0，3，6]作为参数。

每个参数都需要重新训练模型然后测试，因此，参数的选择及其消耗性能，需要谨慎对待

而用于选择参数的集合称为验证集

---------------------------------------------------------------------------------------------------------------------------------

通过评估模型的方法：

均方误差：

将每个预测值 f(xi) 减去数据集里的真实值 yi ，然后取所有的平均值：

误差越小模型越好

还有书上两个没有的方法：平均绝对误差，均方根误差

平均绝对误差，顾名思义，绝对值差的平均值：

均方根误差也就是给均方误差开个根号：

---------------------------------------------------------------------------------------------------------------------------------

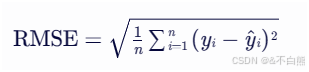
精度和错误率：

精度 + 错误率 = 1

精度就是（预测正确的个数 / 总个数），错误率就是（预测错误的个数 / 总个数）

相对的离散公式为：

---------------------------------------------------------------------------------------------------------------------------------

相对于精度和错误率，用户可能更关心“查准率（precision）”和“查全率（recall）”，就是找出的正样本中有哪些正确的，和正样本中有多少被正确的找出

例如预测出来的好瓜有多少是真的好瓜，和好瓜中有多少被真实预测出

有些书也叫“精确率”和“召回率”

这里引出混淆矩阵：

查准率：TP / TP + FP

查全率：TP / TP + FN

查准率和查全率是一对相对的数值，如果查准率高了那么查全率就低，如果查全率高了查准率就低，只有在一些十分简单的模型中他们才有可能都很高。

如图是P-R曲线：

将样本以模型认为是正例的可能性来从大到小排序，就是图中横轴的排序

也就是说，当查全率为0时，找到的正例一定为真，当查全率为1时，所有的预测都时正例，自然而然查准率就为0

图中根据ABC三个模型绘出的P-R曲线，根据这个曲线，如果有一条线完全包围另一条线，那么就可以认为这个模型更好，除了图像位置，还可以根据平衡点（BEP）的高度来判断模型好坏，例如A>B>C，但是BEP过于简单，有一种更常用的值——F1度量，他可以取代BEP作为模型评判的标准

F1推导的公式为：

而Fβ中，当β越大时，查全率的影响越大，当β为1时，查全率和查准率的影响相同

Fβ的公式：

相对的，当我们需要进行多次测试或者有多个数据集时，我么会得到多个结果

将他们的查准率和全差率进行平均，然后求F1就叫做宏F1，宏查准率和宏全差率

用macro-表示：

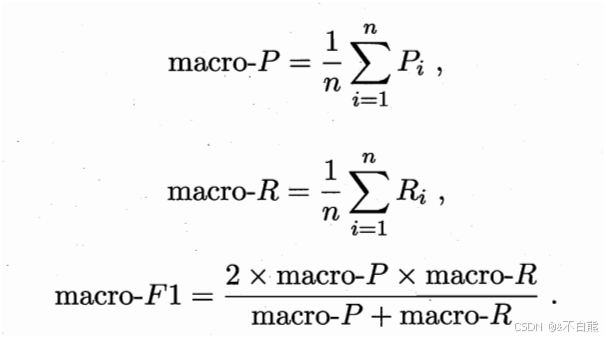
而先将混淆矩阵的TP,FP,TN,FN求平均值，在计算查准率和全差率，叫做微

用micro-表示：

---------------------------------------------------------------------------------------------------------------------------------

真正率（查全率/TPR）和假正率（FPR）：

定义分别为：好瓜中有多少被正确预测的和坏瓜中有多少被正确预测的。

他们绘制的ROC曲线和P-R曲线类似，横轴是FPR，纵轴是TPR。

他们的关系和P-R不同的是TPR和FPR是正比例关系

当某个曲线包住另一个曲线时，就可以说这个模型更好，但是一般通过比较AUC（阴影的面积）来评判模型好坏.

那他的损失就是阴影上面的面积

所以有：

---------------------------------------------------------------------------------------------------------------------------------