二叉树

基本概念

• 结点的度：结点子树的个数，树的度是树中最大的结点度。
• 叶子结点：也叫终端结点，是度为 0 的结点；分枝结点是度不为0的结点。
• 无序树：不考虑子树的顺序，有序树就是不能交换子节点顺序
• 完全二叉树：与相同深度的满树编号相同（只有最后一层不满，且都靠左）
  

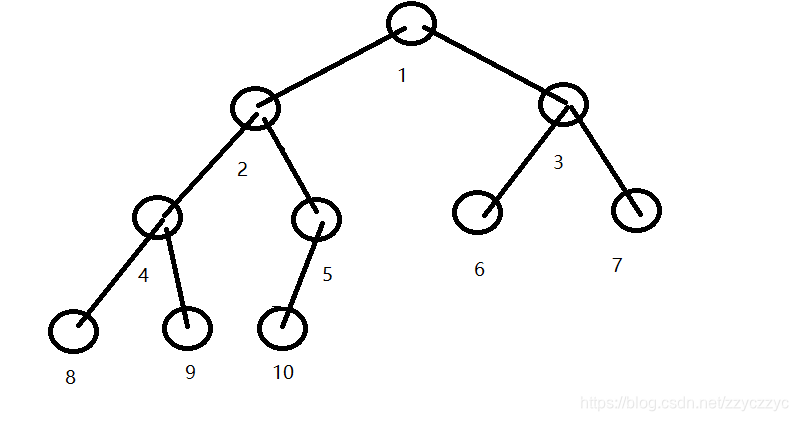
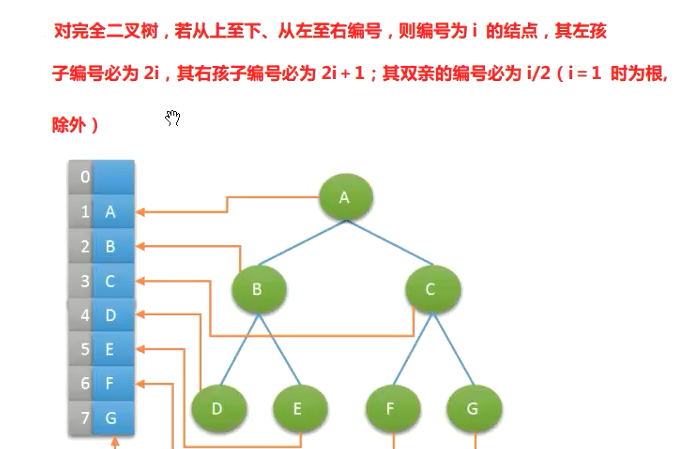
• 普通的树可以通过“左孩子，右兄弟”的结构转化成二叉树

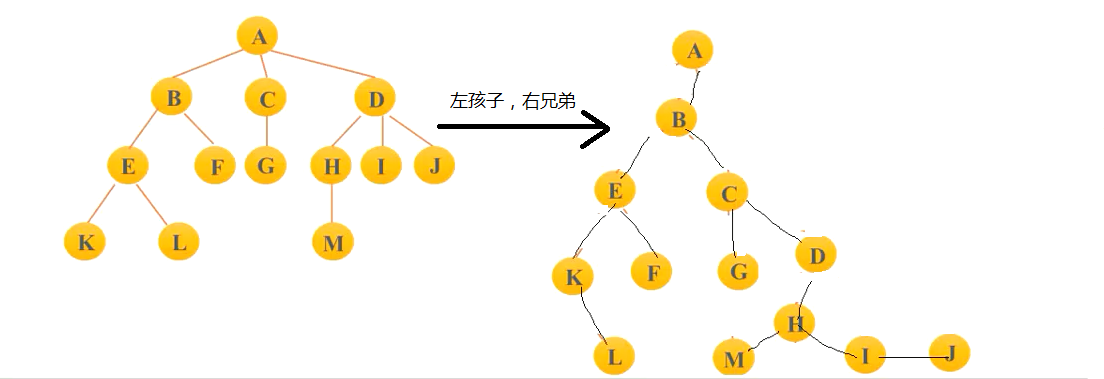
二叉树的遍历

• 二叉树的三种遍历方式（不管哪种都是左在右的前面，先中后指的是当前访问的节点先于子树出现还是后于子树出现）：

1. 先序遍历：根左右

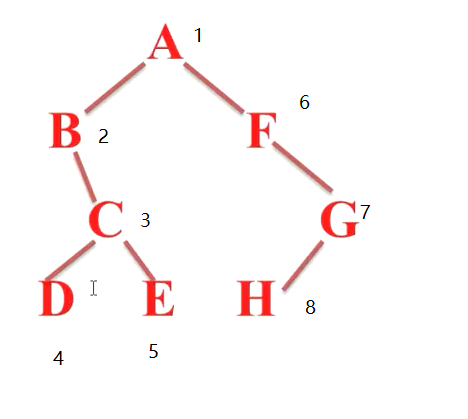
（1）A是树的根，先访问A（根），再到（B）左, 因为B是一个子树，同样遵循这个规则
（2）先访问B（根），再访问左，没有，再访问C（右），C是一个子树，同样遵循这个规则
（3）先访问C（根）， 再D（左），再E（右）
（4）返回A，到F，F是一个子树，先访问F（根），左没有，到G
（5）G同样是子树，先G（根），再到H（左），结束

输出顺序：ABCDEFGH     可以看出根都先于子树

2. 中序遍历：左根右

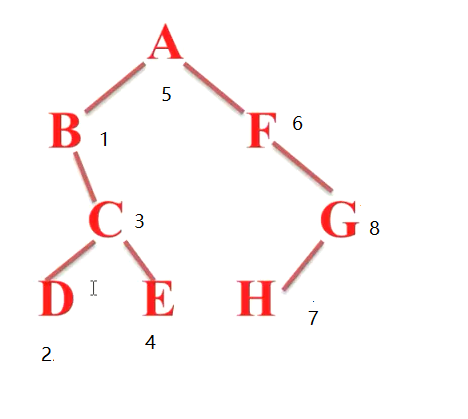
（1）A是一个树的跟，先访问B，B又是一个树的根，
（2）访问左（没有），接着B（根），再到C（右）,C又是一个树的根
（3）先访问D（左）,再访问C（根），再访问E（右）
（4）再到A（总根），再到F，F又是子树
（5）F的左没有，直接就是F（根），再到右，G也是一子树
（6）先H（左），再G（根）

输出顺序：BDCEAFHG    可以看出根都在子树中间

3. 后续遍历：左右根

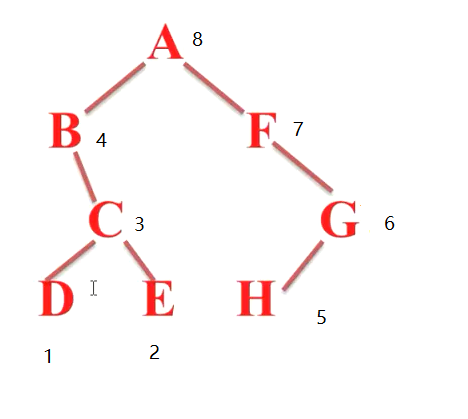
（1）A是一个树的跟，先访问B，B也是一个树的根
（2）B没有左，到C（右），C也是子树
（3）先D（左），再访问E（右），再到C（根）
（4）再到上一个根（B）
（5）再到总树的右F，F是一颗树
（6）先左（没有），再右（G）是一棵树
（7）G这个树，先H（左），再右（没有），再G（根）
（8）再到上一个树F，右输出完了，剩下F（根）
（9）最后剩下根A（总根）

输出顺序：DECBHGFA    可以看出根都在子树后面

---

如何确定一棵树？

1. 通过中序和先序遍历可以确定一颗树
2. 通过中序和后序遍历可以确定一棵树
3. 通过先序和后序遍历不能确定一棵树