Orthogonality and Projection

Orthogonality of the four subspaces

• The row space is perpendicular to the nullspace
• The column space is perpendicular to the nullspace of $A^T$
  
  
• The column space C(A) , a subspace of $R^m$, dimention r
• The leftnull space N($A^T$) , a subspace of $R^m$ ,dimention m-r
• The row space C($A^T$) , a subspace of $R^n$ ,dimention r
• The null space N(A) , a subspace of $R^n$ ,dimention n-r
  
  

Definition of orthogonal subspace

• Two subspace $V$ and $W$ of a vector space are orthogonal if every vector $v$ in $V$ is perpendicular to every vector $w$ in $W$

• Every vector x in the nullspace is perpendicular to every row of $A$, because $Ax=0$ ,the nullspace $N(A)$ and row space $C(A^T)$ are orthogonal subspace of $R^n$
• Every vector $y$ in the nullspace of $A^T$ is perpendicular to every column of $A$, because $A^{T}x=0$ , ,The leftnull space N($A^T$) and the column space C(A) are orthogonal in $R^m$
  
  

Definition of orthogonal complements(正交补)

• The orthogonal complement of a subspace $V$ contains every vector that is perpendicular to $V$

• Nullspace N(A) is the orthogonal complement of the row space C($A^T$) in $R^n$
• LeftNull space N($A^T$) is the orthogonal complement of the column space C(A) in $R^m$

---

Projections

• The projection matrix P（由A得到投影矩阵） multiplies b（被投影的向量） to give p (b在A上的投影) on A

Projection onto a line

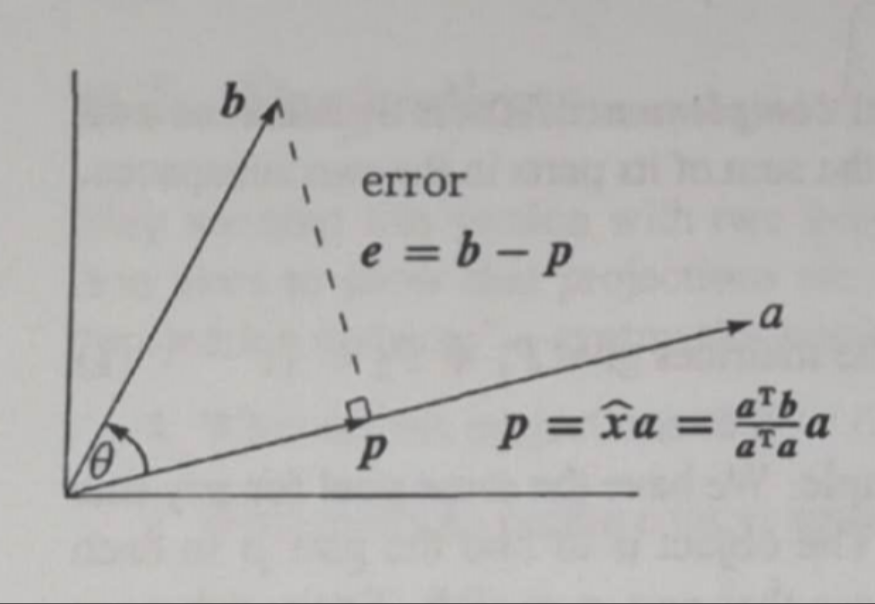
projection matrix :$P=\frac{a{a}^T}{a^{T}a}$

例子：

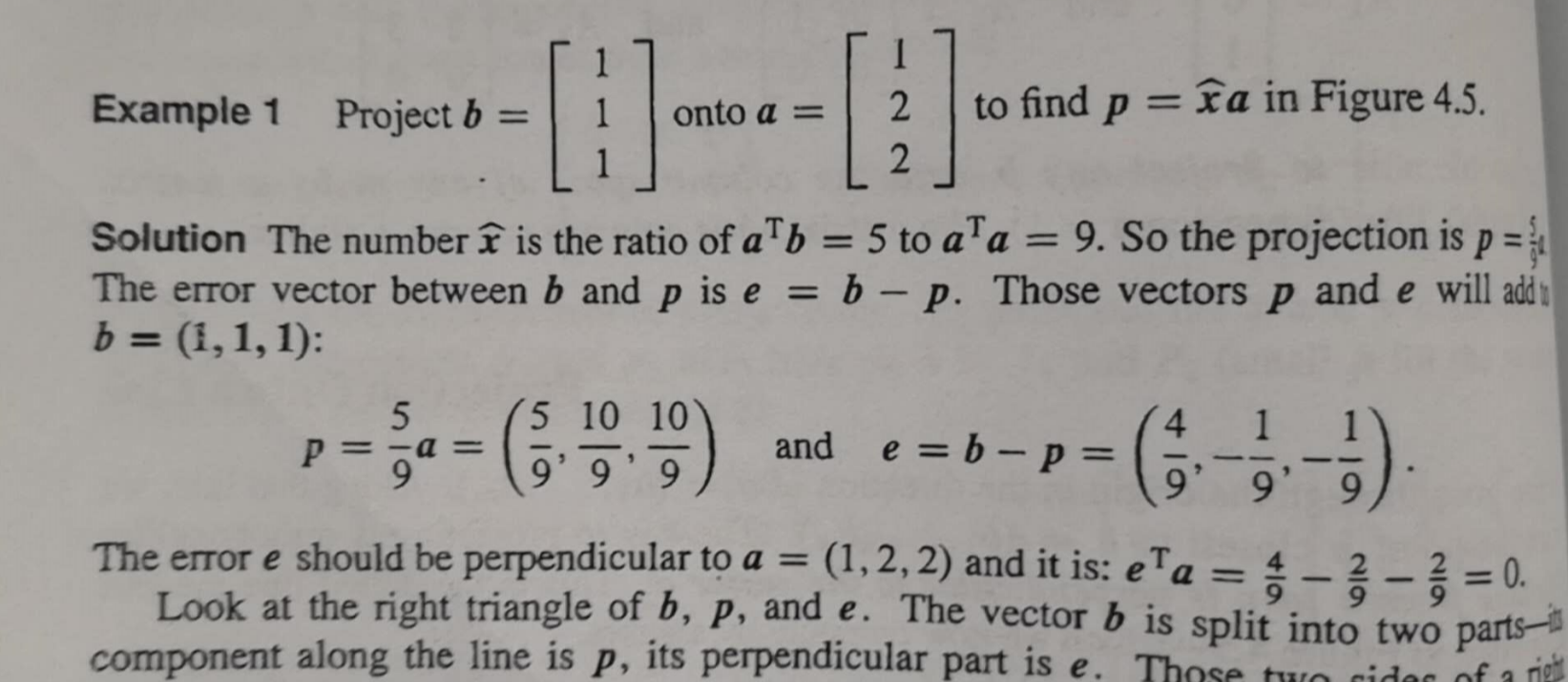
Projection onto a subspace

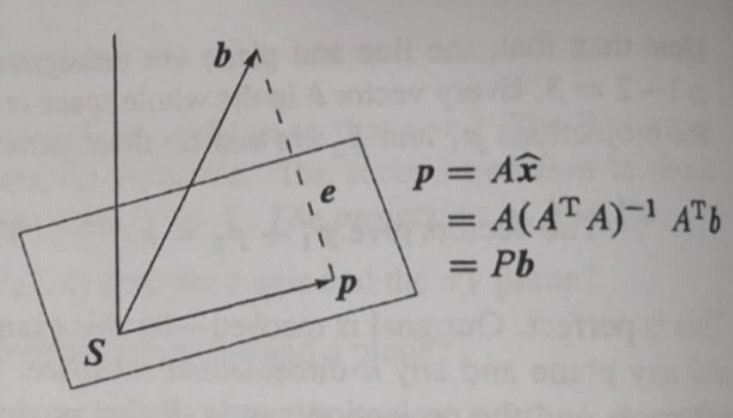
$(I-P)b=e$ :$I-P$ 也是投影矩阵，将b 投影到 plane perpendicular to A to get e

实例

---

Orthogonal bases and Gram-Schmidt

Orthonomal bases and matrix(标准正交基、正交矩阵)

• 标准正交基
  

• (orthogonal matrix)正交矩阵:方阵

由上面标准正交基构成的方阵：正交矩阵

the inverse is the transpose , In the square case we call Q an orthogonal matrix

Projection Using Orthonormal Bases:Q replace A

• Suppose the basis are orthonomal. that means A is Q , $A^{T}A$ is $Q^{T}Q=I$
  投影向量：$p=Q\hat{x}=Q{Q}^{T}b$
  $\hat{x}=Q^{T}b$
  projection matrix:$P=Q{Q}^T$

• When Q is square m=n , (subspace Q is whole space, 任何一个向量投影到整个整个空间，都是其本身，所以投影矩阵是$I$)
  $Q^T=Q^{-1}$
  $\hat{x}=Q^{-1}b$
  projection matrix:$P=Q{Q}^T=I$

The Gram-Schmidt

• 假设 $a,b,c$三个向量不是标准正交基， 转化成正交基（基的长度不是1）$A,B,C$
• 第一步：选$A=a$ ，$B=b-\frac{A^{T}b}{A^{T}A}A=e（误差）$,因为b与A的误差是与A垂直的
• 第二步：$C=c-\frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B$，取c 在$A,B$平面投影的误差e
• 重复下去

例子：