理解汉诺塔中的递归

理解汉诺塔中的递归

##先从一个简单的例子，看看递归的效果。

#include <stdio.h>
void re(int n)
{
    printf("%d",n);
    if(n==1)
    {
        printf("%d",1);
    }
    else
    {
        re(n-1);
    }
    printf("%d",n);
}
int main()
{
    int n;
    scanf("%d",&n);
    re(n);
    return 0;
}

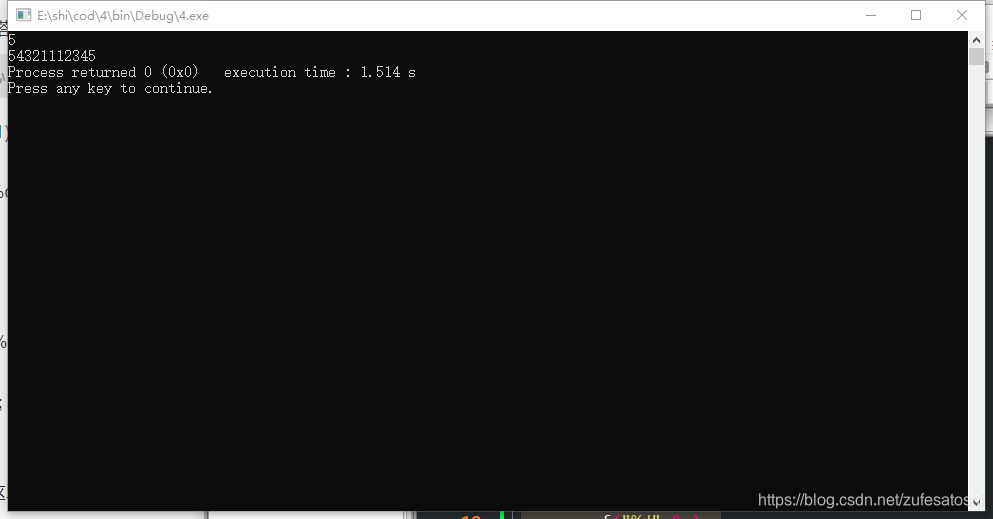
通过以上代码容易发现，此处递归是将n倒推到1，然后再从1~n的结果按照所给的递归公式算出。

在本例中，输出中的第一部分：5 4 3 2 1（是递归过程中输出的），第二部分：1（递归结束的点输出），第三部分：1 2 3 4 5（是根据第一部分得出的递归公式输出的。

注意：n==1的情况

    if(n==1)
    {
        printf("%d",1);
    }

	即递归结束的判断条件，如果此处不写，递归就会一直进行下去。
你会看到如下情况：

下面附上一位知乎（李冰）上的一种比较有趣的讲解：https://www.zhihu.com/question/20507130

说了这么多，回归正题。
约19世纪末，在欧州的商店中出售一种智力玩具，在一块铜板上有三根杆，最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上，条件是一次只能移动一个盘，且不允许大盘放在小盘的上面。
输入
输入为一个整数(小于20）后面跟三个单字符字符串。

整数为盘子的数目，后三个字符表示三个杆子的编号。

输出
输出每一步移动盘子的记录。一次移动一行。

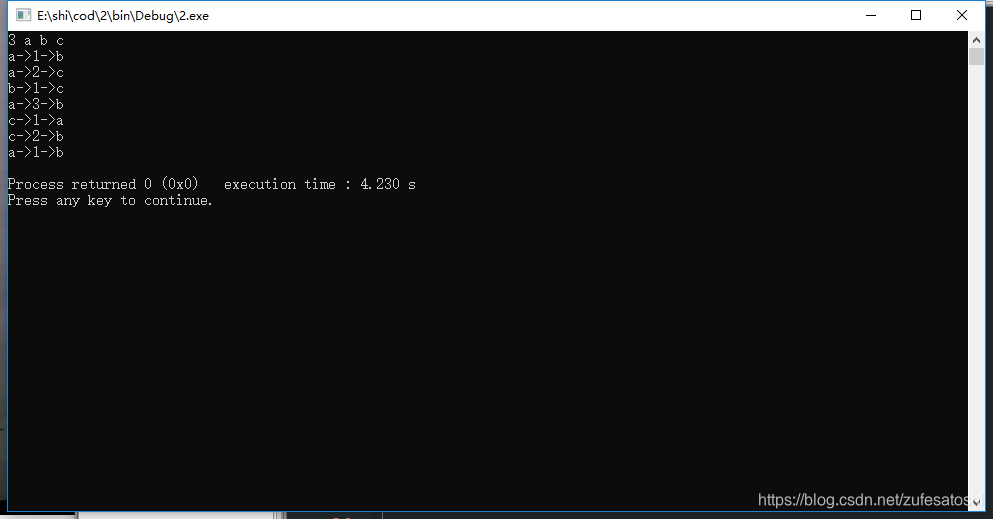
每次移动的记录为例如 a->3->b 的形式，即把编号为3的盘子从a杆移至b杆。
样例输出
a->1->c
a->2->b
c->1->b

先附上我的代码：

#include<bits/stdc++.h>
using namespace std;
int n;
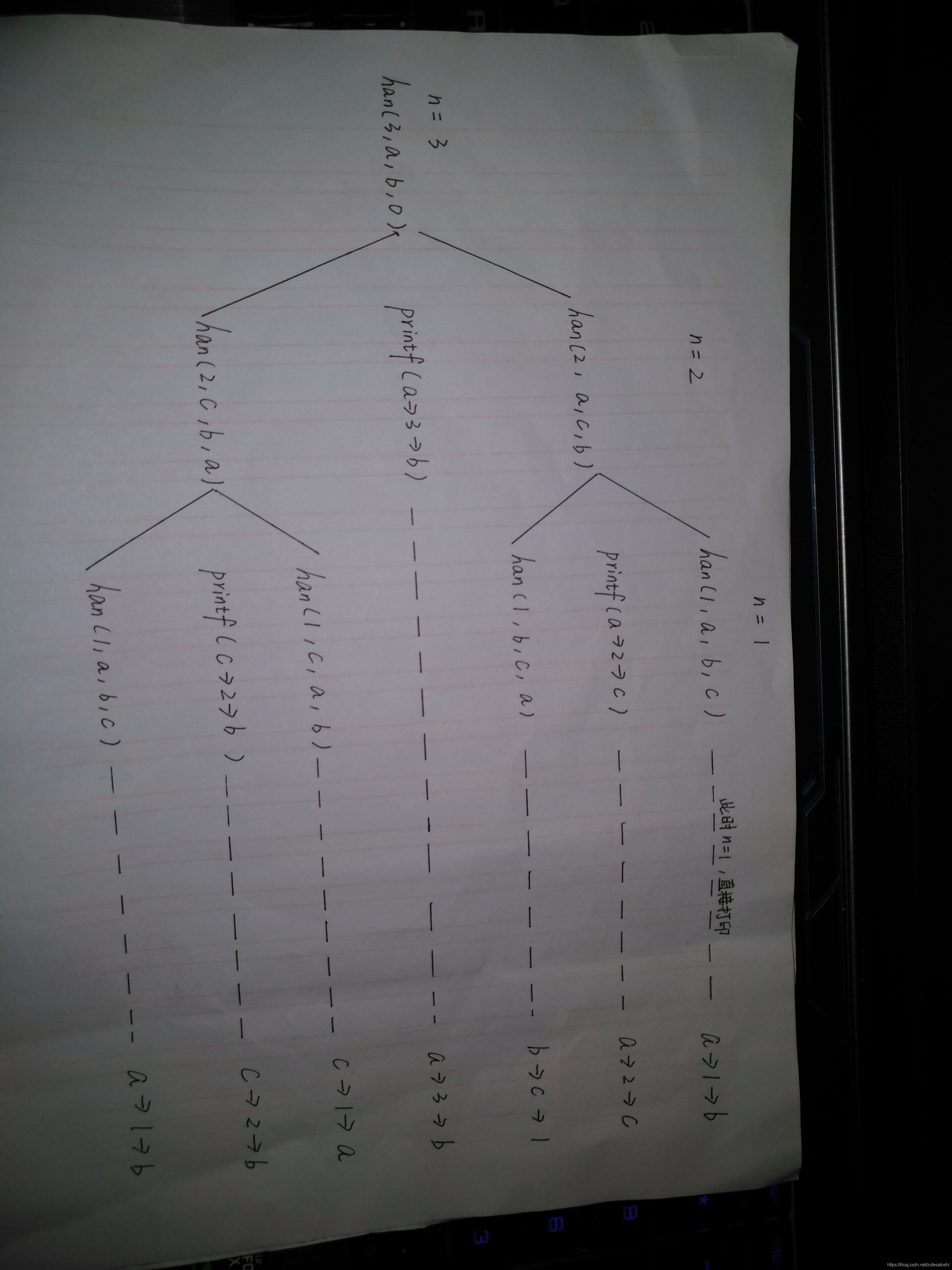
void han(int n,char a,char b,char c)
{
    if(n==1)
    {
        printf("%c->%d->%c\n",a,n,b);
    }
    else
    {
        han(n-1,a,c,b);//先将a中的n-1个盘子放到c盘中,此时a还剩一个最大的盘子，c中有n-1个已经按顺序放好的盘子
        printf("%c->%d->%c\n",a,n,b);//将a中剩下的最大的盘子放到目标b盘中。
        han(n-1,c,b,a);//将c盘中的n-1个盘子放到目标b盘中。
    }
}
int main()
{
    char a,b,c;
    scanf("%d %c %c %c",&n,&a,&b,&c);
    han(n,a,b,c);
    return 0;
}

此处我以输入n=3为例，

总结

1.将问题层层剥皮，理清思路。有点像俄罗斯套娃。
2.实现代码时注意结束判断

第一次写博客，如有错误还请诸位大佬指出。谢谢