机器学习随记【day14】

过拟合问题

以房价为例

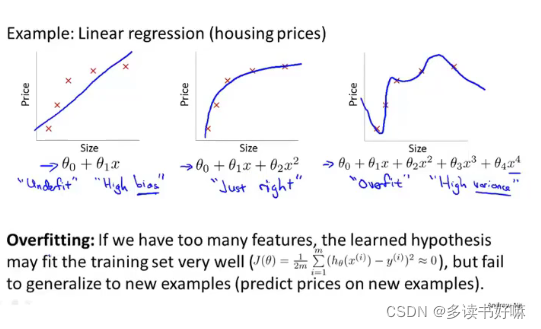
P1:欠拟合，或者说算法有高偏差，即模型没有很好拟合训练数据。
P2:刚好合适。
P3:过度拟合，或者说有高方差，如果我们拟合一个高阶多项式，那么这个函数几乎能拟合所有数据(但是不符合房价的价格规律)。如此函数太过庞大，变量太多。
概括地说，过度拟合将会在变量过多时出现，虽然此时假设能很好拟合数据，代价函数很小，导致他无法泛化(generalize,一个假设模型应用到新样本的能力)到新的样本中，或者说学习器已经把训练样本自身的一些特点当作潜在样本的一般性质。
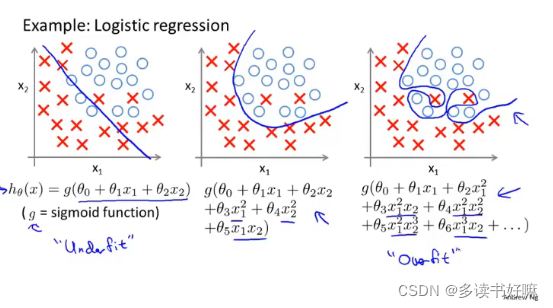
分类问题中也存在此问题

解决

一、减少特征数量
1.人工检查变量清单
2.模型选择算法
此方法在舍弃变量时，也舍弃了关于问题的一些信息
二、正则化
保留特征，减少量级或者参数θj的大小。在有许多变量都对预测值有影响时效果较好

正则化

引入
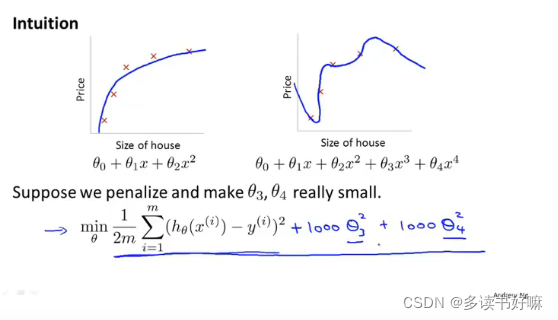
两图都是较好的拟合结果，之前提过P2出现过拟合的情况，泛化的能力不佳。这时为了减小x ^3与x ^4的影响，可以在代价函数中加入惩罚,即图中的形式，+1000θ ^3+1000θ ^4,这样可让两个参数很小
此处的1000指很大的数

正则化思想

简化假设模型，因此也减少了过拟合的情况。
当我们有多个参数，

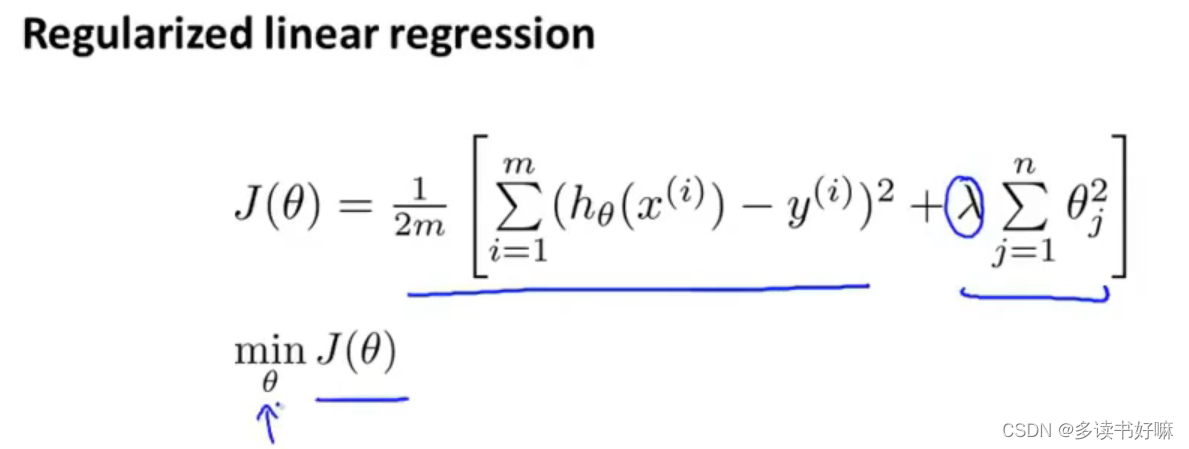
正则化代价函数
当我们有多个参数，而不知道那些需要添加惩罚，就对所有特征添加惩罚，则可以得到以下正则化代价函数:

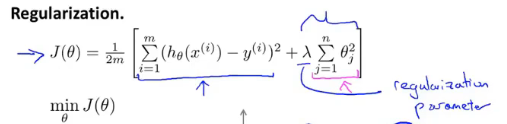
第一项的目的是训练模型更好拟合训练集；第二项目的是保持参数尽可能小，其中从θ0开始累加对结果无影响。
λ:正则化参数，控制两个目标之间的平衡关系

如果对所有特征的惩罚过大(λ过大)，则会导致除θ0外的参数趋0，拟合的曲线为直线，会出现欠拟合的情况。

线性回归正则化

梯度下降

步骤
θ0不参与惩罚

下标非0项也可以写成

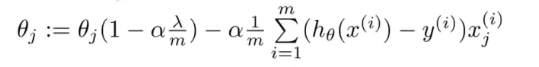
其中θj的系数通常只是略小于1，第二项与之前提到的梯度下降形式一样

正规方程

形式与之前提到类似，加入了一个n+1维的方阵，并且相加后的方阵一定可逆。

逻辑回归正则化

逻辑回归在加入惩罚后的代价函数

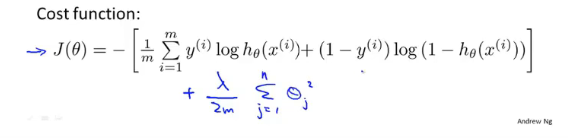
梯度下降

步骤
形式与上文的相同

高级优化算法

代码实现
对于这些算法，我门只需要自己定义一个costFunction 函数，在运行时调用库里有的算法函数即可，如fminuc函数。