机器学习随记【day11-day13】

多读书好嘛

已于 2022-01-26 23:54:38 修改

阅读量530

点赞数

CC 4.0 BY-SA版权

文章标签：机器学习

于 2022-01-21 23:32:32 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/ztyLOVElearning/article/details/122631059

本文探讨了监督学习中的分类与回归问题，对比了线性回归与逻辑回归在解决分类问题上的表现，详细介绍了逻辑回归模型及其假设函数、决策边界、代价函数等内容。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

分类问题

与回归问题同属于监督学习，区别在于预测离散值的输出、
在这里插入图片描述
用线性回归解决分类问题
可以假设输出阈值为0.5，大于0.5则预测1，反之预测0。
若添加一个没有提供任何信息系得样本，线性回归对数据得拟合直线会因此改变，偏离正确直线；此外，假设函数的输出值会远大于1或远小于0，即使所有样本的训练标签都是0或1。因此通常不用线性回归解决分类问题。
在这里插入图片描述

逻辑回归

模型
假设函数：hθ (x)=g(θ^TX)
其中g(x) :Sigmod函数/Logistic函数
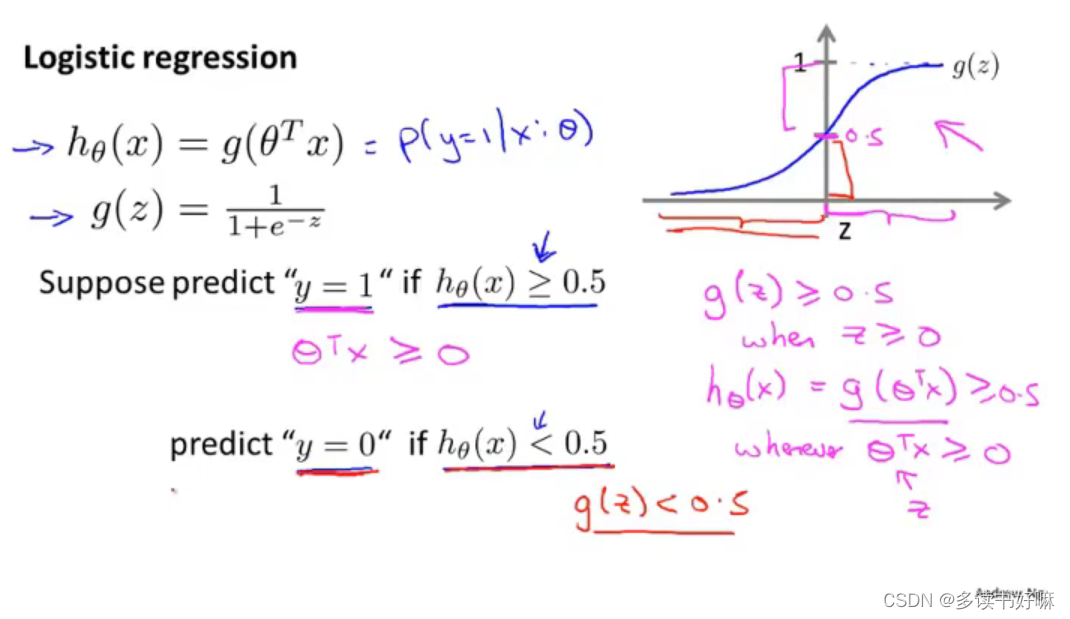
在这里插入图片描述

在这里插入图片描述

决策边界

强调：决策边界不是训练集的属性，是假设函数本身以及其参数的属性。不是用训练集来定义决策边界，我们用训练集来你和参数θ。
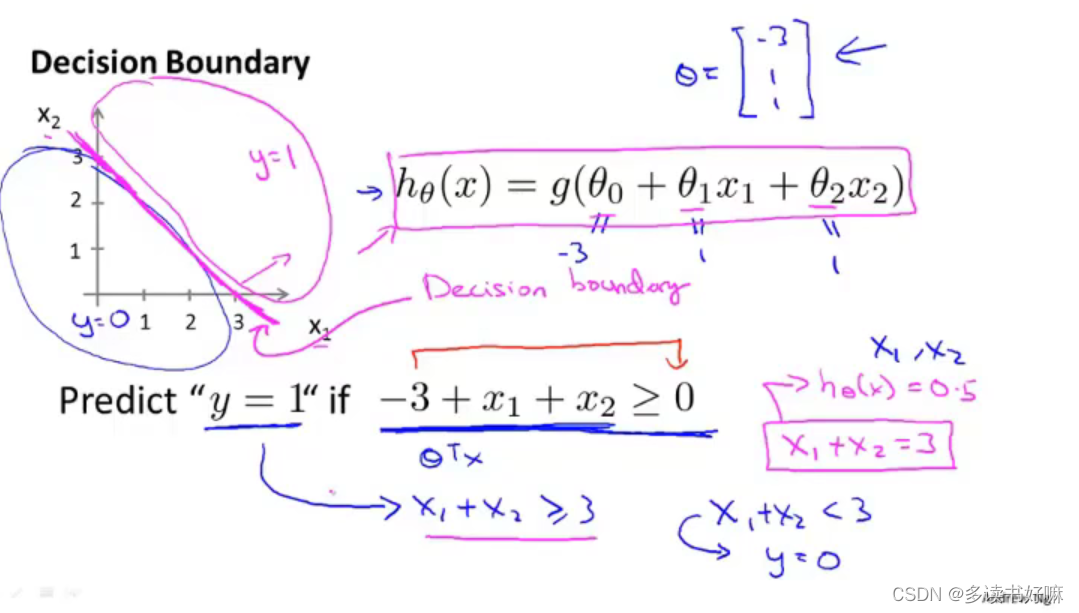
在这里插入图片描述
通过添加多项式，可以得到更加复杂的决策边界。

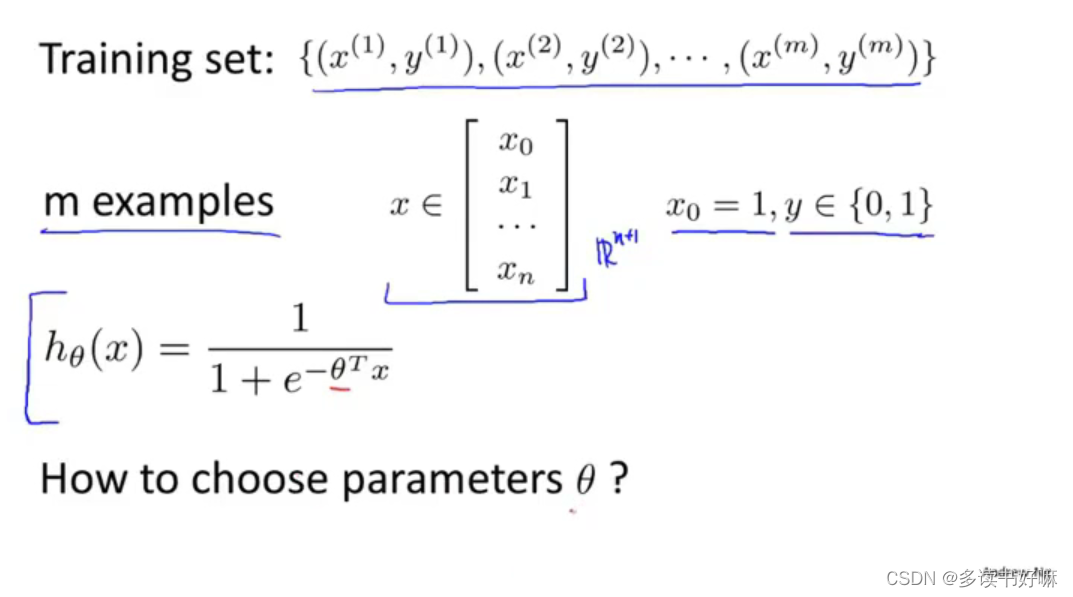
在这里插入图片描述

代价函数

在这里插入图片描述
若采用线性回归的形式，sigmoid函数会导致J(θ)非凸，产生许多局部最小值

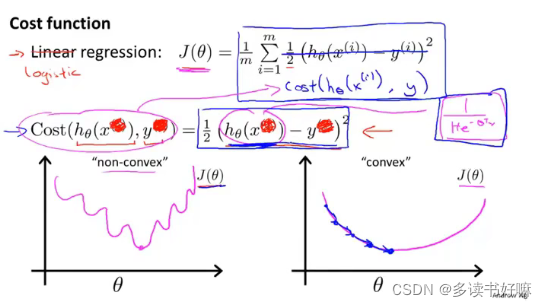
用以下形式表示代价函数能很好解决

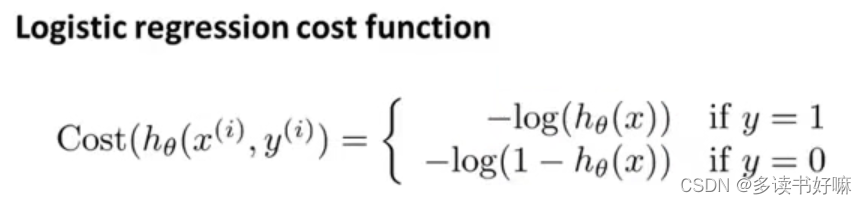
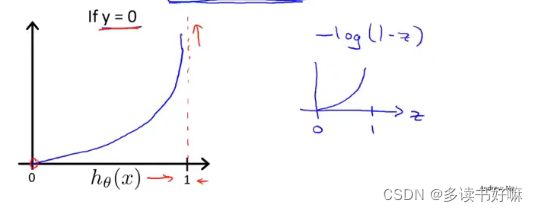
简化形式

在这里插入图片描述

梯度下降

形式类似线性回归
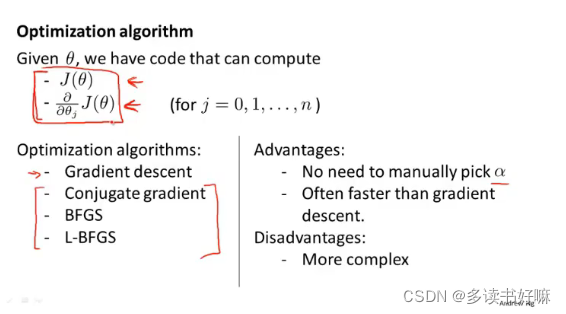
在这里插入图片描述

高级优化

在这里插入图片描述
下三者涉及其他领域，思路是给出计算导数项和代价函数的方法，你可以认为算法有一个智能的内部循环,事实上，他们确实有一个智能的内部循环,称为线性搜索算法(line search)，它可以自动尝试不同的学习速率，并自动选择一个好的学习速率，它甚至可以为每次迭代选择不同的学习速率，那么你就不需要自己选择。他们更复杂、高级，因而通常比梯度下降更快地收敛。

举例
在这里插入图片描述

多元分类:一对多

类别多分类
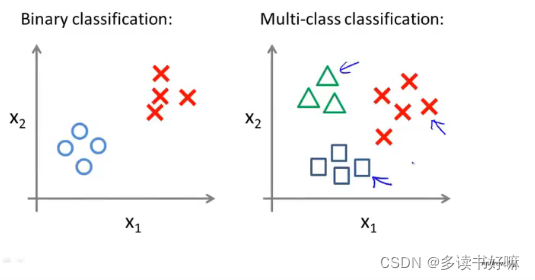
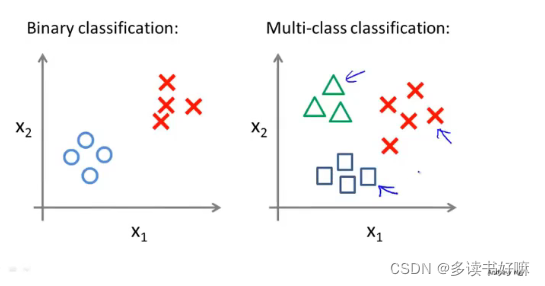
在这里插入图片描述

二元分类与多元分类数据集比较

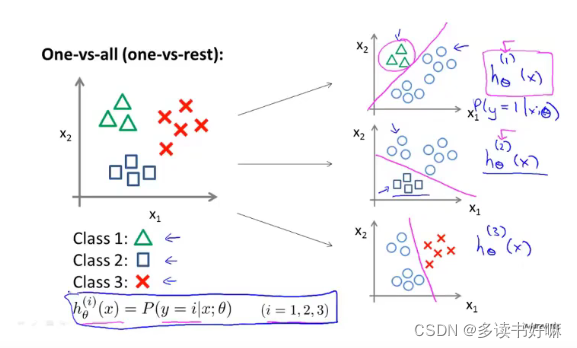
多元分类步骤
训练一个逻辑回归分类器hθ^(i)(x)预测i类别y=1地概率。最后为了预测，我们将新输入值x输入给分类器运行，选择h最大地类别
**加粗样式**
在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。