4020. 【雅礼联考DAY02】Revolution

最新推荐文章于 2020-04-29 14:47:41 发布

lazy-sheep

最新推荐文章于 2020-04-29 14:47:41 发布

阅读量205

点赞数 2

CC 4.0 BY-SA版权

分类专栏： # 网络流

本文链接：https://blog.youkuaiyun.com/zsjzliziyang/article/details/104282423

网络流专栏收录该内容

3 篇文章

订阅专栏

本文探讨了一种在有限网格地图上进行投资以实现收益最大化的算法。通过构建最小割模型，文章详细解释了如何在考虑四连通格子的投资与收益关系下，使用网络流算法求解最优解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

地图是个矩形的网格。
可以花费一定金钱在一些格子投资。
被投资的格子或者四连通的格子都被投资的话，我就可以获得该格子的收益。
利益最大化是作为商人的基本准则，但这是计算机的任务，拜托您了。

Input

第一行两个数 n,m(n,m ≤ 20)，表示矩形的长和宽。
接下来 n 行，每行是 m 个字符组成的字符串，描述投资的花费。
接下来 n 行，每行是 m 个字符组成的字符串，表示该格子的收益。
花费和收益按照一种奇葩的方式给出：
字符数
‘0’ -’ 9’ 0-9
‘a’ -’ z’ 10-35
‘A’ -’ Z’ 36-61

Output

一个数，表示收益的和减去投资的和的最大值。

Sample Input

【样例 1】
2 2
21
12
21
12
【样例 2】
2 2
ZZ
ZZ
11
11
【样例 3】
3 3
XXX
XXX
XXX
aaa
aZa
aaa
【样例 4】
2 4
asam
atik
123A
45BC
【样例 5】
9 8
IIIIIIII
IIWWWWII
IIWIIIII
IIWIIIII
IIWWWWII
IIIIIWII
IIIIIWII
IIWWWWII
IIIIIIII
IIIIIIII
II0000II
II0II0II
II0II0II
II0000II
II0II0II
II0II0II
II0000II
IIIIIIII

Sample Output

【样例 1】4
【样例 2】0
【样例 3】2
【样例 4】71
【样例 5】606

Data Constraint

n,m ≤ 20.

Solution

考虑最小割模型。

答案=所有的收益-最小割。

那么最小割的任务就是求出每个点选或不选的最小的花费。

首先每个点选的话就要割掉费用的边，如果不选就要割掉收益。也就是说每个点的cost[i]和profit[i]是二选一的关系。

那么它们是“串联”的关系，如图。

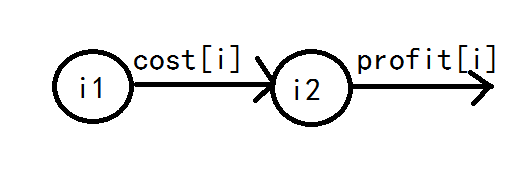
这样就表达了 “花费一定代价来购买这个格子” 和 “舍弃这个各自的代价” 之间的 “或” 关系。那么，我们知道对于一个点是不可能同时割掉它的profit和cost的，因为这样一定不优。

可是这里还有一个特殊的关系那就是，如果四联通的格子都被选了，那么这个格子的收益也可以获得（也就是不用割这个点的收益的边。）

那么我们考虑将矩阵内划分成黑白两类点，保证黑色点的四联通点都是白点，白点的四联通点都是黑点。

对于4个黑点的cost都被删掉的话，那么被包围的白点就可以不选，也就是S到T的路径是不连通的（S不能通过白点到达T）。

那么我们必须将黑点接在白点路径的后面。并且将S连向白点，黑点连向汇点T。

就像这样

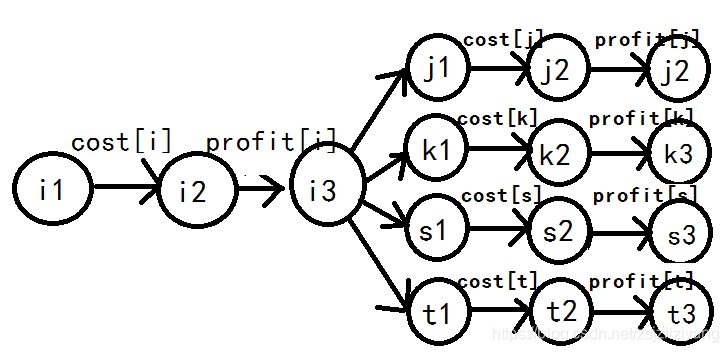
其中，i是白点，j,k,s,t是i的四联通的黑点，到目前为止我们的图是符合了上面提到的要求。

但是，如果4个黑点的profit都被割掉时，白点i必须在割掉花费或者收益中二选一，那么就意味着S可以通过被包围的白点到T。

那么我们将所有黑点的profit连到1号点前面，所以我们将图调成为如下：

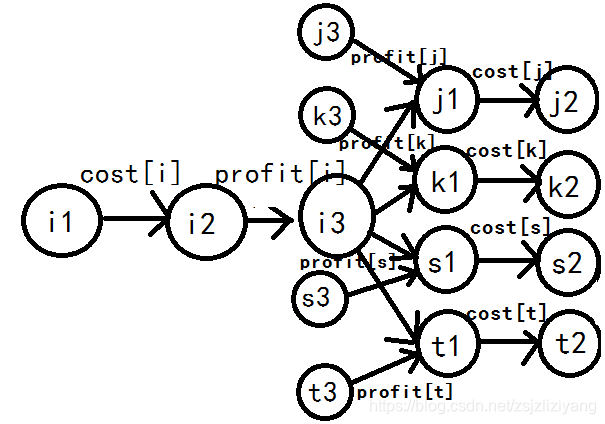
之前我们知道割掉了j,k,s,t的profit就不能再割它们的cost，那么就只能在i的cost和profit中选择，这是符合上面的要求的。但是很明显这个图还有缺陷，比如j3,k3,s3,t3必须有边连向它们，但是又不能是源点S，那么我们继续构图。

然后我们考虑对于每个黑点，这个要求依然成立。

也就是将其四联通的白点的cost割掉后它与T不连通，而将其四联通白点的profit割掉后它与T仍然联通。如下图：其中abci是白点、j是黑点。

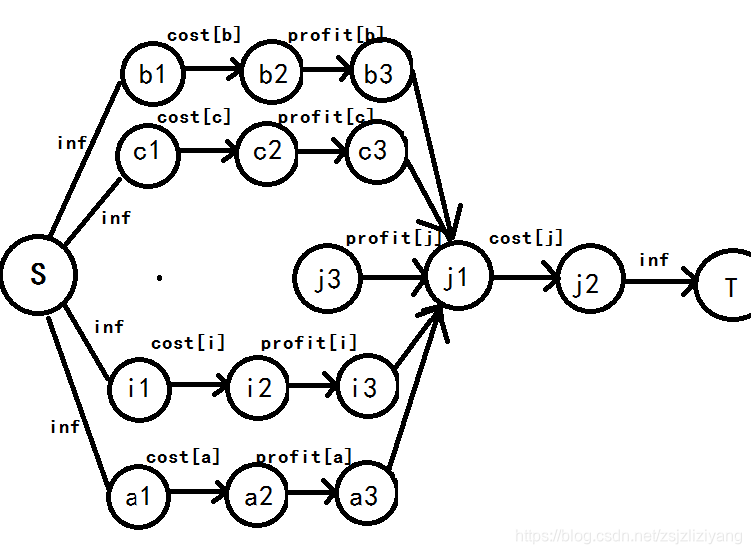
为了满足将其四联通白点的cost割掉后，S不能通过黑点j到达T，那么我们必须从a,b,c,i的cost的后面的点开始连边，而为了满足将黑点四联通的白点的profit割掉后，S仍然可以通过黑点j到达T，那么我们必须从a,b,c,i的profit的前面开始来连边，那么我们就从a2,b2,c2,i2向黑点j3连一条inf的边就可以了。

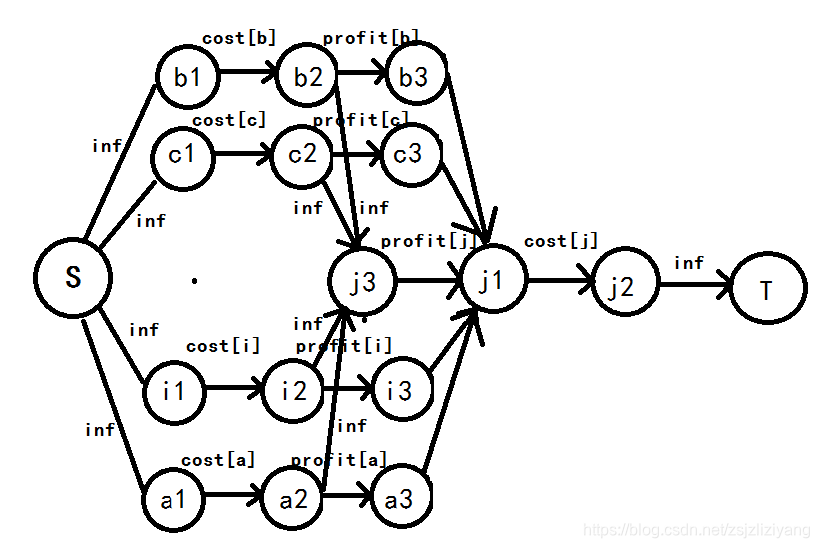
至此，如果你看懂了整个思路，那么你也应该会构图了，这样的图符合了所有的要求。

那么最后只要再跑一遍最大流求出最小割就可以了。

时间复杂度为网络流的(N^2M)。

Code

#include<cstdio>
#include<cstring>
#include<algorithm>
#define I int
#define F(i,a,b) for(register int i=a;i<=b;++i)
#define mem(a,b) memset(a,b,sizeof a)
#define N 5000
using namespace std;
I n,m,x,y,q[N*2],d[N],fx[4][2]={{1,0},{0,1},{-1,0},{0,-1}},ans,flow;
I t[N*2],nx[N*2],s[N*2],ls[N],tot=1,S,T,inf=2147483647;
char c;
I id(I x,I y){return ((x-1)*m+y-1)*3;}
void add(I x,I y,I z){F(i,1,2){t[++tot]=y,nx[tot]=ls[x],ls[x]=tot,s[tot]=z;swap(x,y);z=0;}}
void work(){
	scanf("%c",&c);
	if(c>='0'&&c<='9') x=c-'0';
	else if(c>='a'&&c<='z') x=10+c-'a';
	else if(c>='A'&&c<='Z') x=36+c-'A';
}
I bfs(){
	mem(d,0),mem(q,0);
	d[q[1]=S]=1;
	I i=0,j=1;
	while(i<j){
		x=q[++i];
		for(I k=ls[x];k;k=nx[k]) if(!d[y=t[k]]&&s[k]>0){
			d[q[++j]=y]=d[x]+1;
			if(y==T) return 1;
		}
	}
	return 0;
}
I dinic(I x,I rest){
	if(x==T) return rest;
	I p=0,z;
	for(I k=ls[x];k;k=nx[k]) if(d[z=t[k]]==d[x]+1&&s[k]){
		I f=dinic(z,min(rest-p,s[k]));
		if(!f) d[z]=0;
		s[k]-=f,s[k^1]+=f;
		p+=f;
	}
	return p;
}
I main(){
	scanf("%d%d\n",&n,&m);S=n*m*3+1,T=S+1;I z;
	F(i,1,n){
		F(j,1,m){
			work();z=id(i,j);
			if((i+j)&1){
				add(S,z+1,inf);
				add(z+1,z+2,x);
				F(k,0,3){
					x=i+fx[k][0],y=j+fx[k][1];
					if(x>0&&y>0&&x<=n&&y<=m){add(z+2,id(x,y)+1,inf),add(z+3,id(x,y)+2,inf);}
				}
			}
			else{add(z+2,z+3,x),add(z+3,T,inf);}
		}
		scanf("\n");
	}
	F(i,1,n){
		F(j,1,m){
			work();z=id(i,j);
			if((i+j)&1) add(z+2,z+3,x);
			else add(z+1,z+2,x);
			ans+=x;
		}
		scanf("\n");
	}
	while(bfs()){
		while(flow=dinic(S,inf)) ans-=flow;
	}
	printf("%d\n",ans);
	return 0;
}