染色法判定二分图 竟然这么简单

说明：优快云和公众号文章同步发布，需要第一时间收到最新内容，请关注公众号【比特正传】。

0、概念解释

二分图：将图中n个顶点分为两个互不相交的子集A和B，每条边所关联的两个顶点u和v分别在两个不同的子集中，这样的图可以称为二分图。

二分图不存在奇数环（充分必要条件）

1、问题描述

背景：
我发现洛谷上竟然没有二分图判定的模板题，这很不利于初学者的学习，因此我做了一点微薄的贡献，提供了一道判定二分图的模板题，并配置了20个测试用例。

题目链接：
https://www.luogu.com.cn/problem/U425878

2、染色法算法描述

染色法，顾名思义，就是给每个节点染色，由于是二分图，因此我们有两种颜色，比如颜色1和颜色2，通过dfs或者bfs搜索的时候，给每个节点进行染色，如果染色过程中，出现冲突，比如一条边相连的两个节点u和v都是同一个颜色，那么说明不是二分图，返回false即可，如果搜索完后，每个节点都有了颜色，并且没有出现冲突，那么说明就是二分图。

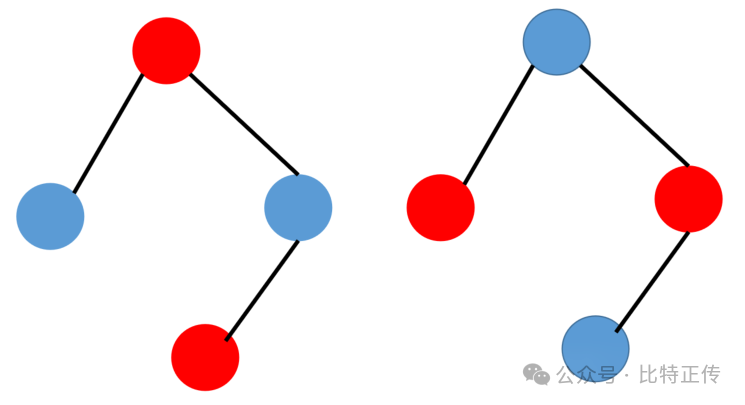
如下图是一个二分图

如下图不是一个二分图

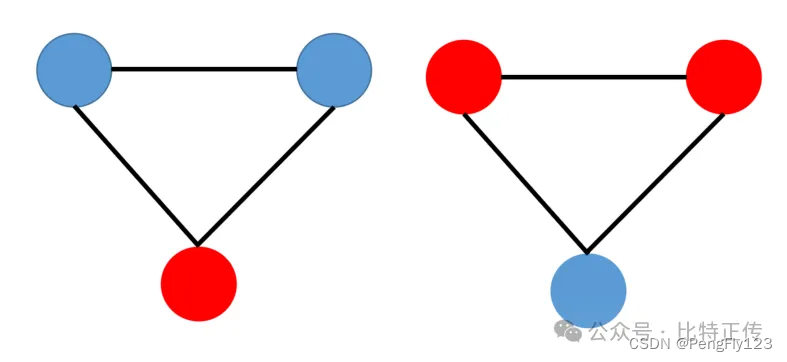
上图无论如何染色，总有两个相邻节点是同一个颜色，因此不是二分图。

3、AC code

下面分别通过dfs和bfs来实现染色法判定二分图，可以结合代码及注释进行理解。

DFS搜索

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+7;
int n, m, u, v; 
vector<int> g[N];
int color[N];
// x为当前节点，c为当前颜色，取值为 1 或 2 
bool dfs(int x, int c) {
  color[x] = c;    // 染色 
  for(int ne : g[x]) {  // 然后搜索x节点的相邻节点进行染色 
    if(!color[ne]) {  // 没有染过色，那就染色并搜索 
      if(!dfs(ne, 3-c)) return false;  // 3-c可以将1变为2,2变为1 
    } else if(color[ne] == color[x]) return false;  // 已经染过色了，但是和x是一个色，出现冲突了，返回false 
  }
  return true;  // 全程没有出现冲突，那么返回true 
}
int main() {
  cin >> n >> m;
  for(int i=1; i<=m; i++) {
    cin >> u >> v;
    g[u].push_back(v);  // 无向图 
    g[v].push_back(u);
  } 
  bool flag = true;  // 标记是否为二分图 
  for(int i=1; i<=n; i++) {  // 因为有可能是不连通图，所以每个连通块都需要搜索一次 
    if(color[i]) continue;  // i所在的联通块已经染过色了，就跳过 
    if(!dfs(i, 1)) {  // 如果染色过程中返回了false，那说明出现了矛盾，就不是二分图 
      flag = false;  // 标记为不是二分图 
      break;  // 可以结束循环了 
    }
  }
  if(!flag) cout << "No";
  else cout << "Yes";
  return 0;
}

BFS搜索

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+7;
int n, m, u, v; 
queue<int>q;
vector<int>g[maxn];
int color[maxn];
bool bfs(int x)
{
  q.push(x);  //先放入当前点 
  color[x]=1;   //上色 
  while(!q.empty()){
    int v=q.front(); q.pop();
    for(int ne : g[v]) {
      if(color[ne] == 0) {
        color[ne] = 3-color[v];//没有标记过就标记上与v相反的颜色
        q.push(ne);
      }else if(color[v] == color[ne]) return false;
    }
  }
  return true;
}
int main() {
  cin >> n >> m;
  for(int i=1; i<=m; i++) {
    cin >> u >> v;
    g[u].push_back(v);
    g[v].push_back(u);
  } 
  bool flag = true;  // 标记是否为二分图 
  for(int i=1; i<=n; i++) {  // 因为有可能是不连通图，所以每个连通块都需要搜索一次 
    if(color[i]) continue;  // i所在的联通块已经染过色了，就跳过 
    if(!bfs(i)) {  // 如果染色过程中返回了false，那说明出现了矛盾，就不是二分图 
      flag = false;  // 标记为不是二分图 
      break;  // 可以结束循环了 
    }
  }
  if(flag) cout << "Yes";
  else cout << "No";
  return 0;
}

动手做起来吧！