题目:
骑士厌倦了一次又一次地看到相同的黑白方块,并决定
环游世界。每当骑士移动时,它都是一个方向上的两个正方形和一个垂直于此方向的正方形。骑士的世界就是他所生活的棋盘。我们的骑士住在一个棋盘上,这个棋盘的面积比普通的8 * 8棋盘小,但它仍然是矩形的。你能帮助这个冒险的骑士制定旅行计划吗?问题 找到一条道路,使骑士访问每个方块一次。
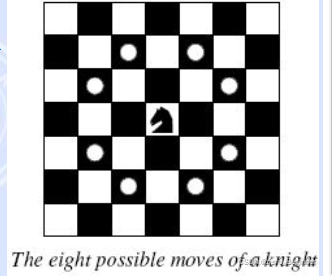
输入:
输入以第一行中的正整数 n 开头。以下行包含 n 个测试用例。每个测试用例由一行具有两个正整数 p 和 q 组成,使得 1 <= p * q <= 26。这表示一个 p * q 棋盘,其中 p 描述有多少个不同的平方数 1, . . . , p 存在, q 描述存在多少个不同的方形字母。这些是拉丁字母表的前q个字母:A,...
输出:
每个方案的输出都以包含"方案#i:"的行开头,其中 i 是从 1 开始的方案编号。然后打印一行,其中包含字典学上的第一条路径,该路径访问棋盘的所有方块,骑士移动,然后是空行。路径应通过连接所访问的正方形的名称在一条线上给出。每个正方形名称由一个大写字母后跟一个数字组成。
如果不存在这样的路径,则应在一行上输出不可能。
示例输入
3 1 1 2 3 4 3
示例输出
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4.
设计思路:
要遍历所有走的格子数,就要利用到深度优先搜索,首先我们定义骑士8个可走的位置,用flag来标志骑士能否走完所有格子。首先定义dfs函数,先判断m*n是否走完所有格子,若走完flag则置为1,若没走完,则进行深搜,看下一个位置能否走。main函数里面的memset表示将数组置为0,特别对于字符型数组,不清空,输出的时候,很可能是乱码。
代码如下:
#include<iostream>
#include<string.h>
using namespace std;
int a[30][30];
int step[8][2] = { {1,2},{1,-2},{2,1} ,{2,-1},{-1,2},{-1,-2},{-2,-1},{-2,1} };//骑士可以走的八个位置坐标
int m, n, book[100][2];//遍历骑士所走的位置
bool flag = 0;//判断是否完成
void dfs(int x, int y, int t) { //t为格子数目
if (t == (n * m)) { //判断所有的格子是否被遍历完全
flag = 1;
return;
}
if (flag == 1)
return;
for (int i = 0; i < 8; i++) {
int tx = x + step[i][0], ty = y + step[i][1]; //当前位置
if (a[tx][ty] == 1) //如果走过了就遍历为1
{
a[tx][ty] = 0; //走过了不能再走了,遍历为0
book[t][0] = tx;
book[t][1] = ty;
dfs(tx, ty, t + 1); //进行深搜
if (flag == 1) //如果找到路径了,则跳出循环
break;
a[tx][ty] = 1; //若道理不通就进行回溯
}
}
return;
}
int main()
{
int x;
cin >> x;
for (int i = 1; i <= x; i++) {
flag = 0; //记录是否找到路径
memset(a, 0, sizeof(a)); //将数组初始化为0
memset(book, 0, sizeof(book));
cin >> m >> n;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
a[i][j] = 1; //6将所走的地方标记为1
a[1][1] = 0;
dfs(1, 1, 1);
book[0][0] = 1;
book[0][1] = 1;
cout << "scenario #" << i << ":" << endl;
if (flag == 1)
{
for (int i = 0; book[i][1] != 0; i++)
{
cout << (char)(book[i][1] - 1 + 'A') << book[i][0];
}
cout << endl;
}
else
cout << "impossible" << endl;
cout << endl;
}
}
运行结果:
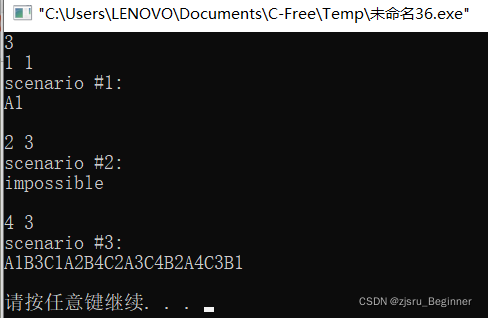





 本文介绍了如何使用深度优先搜索算法解决POJ-2488问题,即找到一条路径让骑士在给定的矩形棋盘上每个方块恰好访问一次。文章提供了题目描述、设计思路和代码实现,展示了如何通过DFS遍历所有可能的路径并判断是否存在可行解。
本文介绍了如何使用深度优先搜索算法解决POJ-2488问题,即找到一条路径让骑士在给定的矩形棋盘上每个方块恰好访问一次。文章提供了题目描述、设计思路和代码实现,展示了如何通过DFS遍历所有可能的路径并判断是否存在可行解。
















 1747
1747

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








