洛谷P-1044 栈

题目：

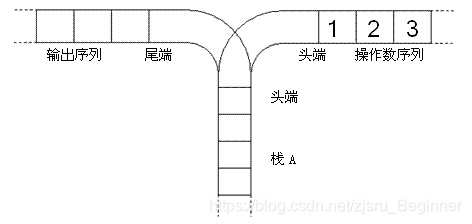
宁宁考虑的是这样一个问题：一个操作数序列，1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 n。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

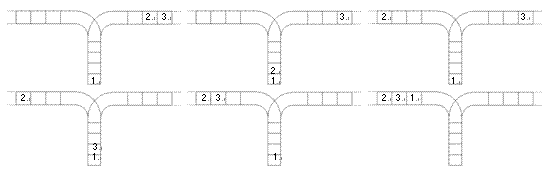
使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

（原始状态如上图所示）

你的程序将对给定的 n ，计算并输出由操作数序列1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式：

输入文件只含一个整数 n（1 ≤ n ≤ 18）。

输出格式：

输出文件只有一行，即可能输出序列的总数目。

输入输出样例：

输入#1：

3

输出#1：

5

分析： 

题目大意为：给出一个数 n ，求 1 , 2 , 3 ,..., n  随机入栈出栈后的不同排序情况有几种。

• n = 1

        1个数字随机入栈出栈情况为1。

• n = 2

        2个数字随机入栈出栈情况为：12,21；

        结果 = 2;

• n = 3

        3个数字随机入栈出栈情况为：

        数字1在第一个位置，数字2,3排序情况有2种：1,2,3/1,3,2；

        数字1在第二个位置，数字1前的数字必是2，排序情况有1种：2,1,3；

        数字1在第三个位置，数字2,3排序情况有2种：2,3,1/3,2,1；

        结果 = 5;

• n = 4

        4个数字随机入栈出栈情况为：

        数字1在第一个位置，其余数字排序情况5种；

        数字1在第二个位置，数字2必在数字1前，其余数字排序情况2种；

        数字1在第三个位置，数字4必在数字1后，其余数字排序情况2种；

         数字1在第四个位置，其余数字排序情况5种；

        结果 = 14;

总结：1,2,5,14...符合卡特兰数；

卡特兰数：

  是一种经典的组合数，经常出现在各种计算中，其前几项为 : 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

其符合递推式：

h(n) = h(0) * h(n-1) + h(1) * h(n-2) + ... + h(n-1) * h(0) ( n ≥ 2 )

于是这道题转变成了求 卡特兰数 的题目。

AC代码：

#include<iostream>
using namespace std;
int main()
{
	int n, i, j;
	int f[20] = {0};
	f[0] = f[1] = 1;
	cin >> n;
	for (i = 2; i <= n; i++)
		for (j = 0; j < i; j++)
			f[i] += f[j] * f[i - 1 - j];
	cout << f[n];
}

---

cs202 fanyuchen