pLSA图模型
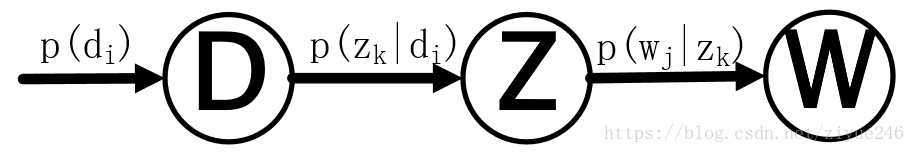
求解目标p(W,D) ,整个文档集合的出现概率,使得p(W,D) 最大化,即为plsa的目标:
下面咱们开始求解p(W,D):
为 词wj在文档di中出现的次数;
注释: 为第m篇文档中,第n个词出现的概率,
为第i篇文档中词表中第i个词出现的概率,由于di
利用EM算法求
至此,我们就可以用em算法迭代求解了
其中、
需要用偏导数
=0求出
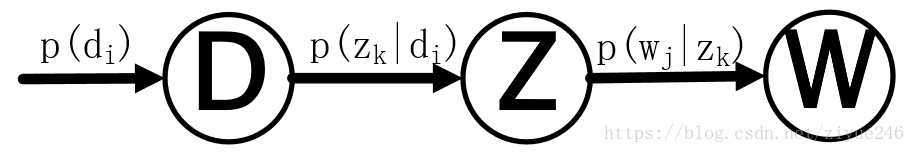
求解目标p(W,D) ,整个文档集合的出现概率,使得p(W,D) 最大化,即为plsa的目标:
下面咱们开始求解p(W,D):
为 词wj在文档di中出现的次数;
注释: 为第m篇文档中,第n个词出现的概率,
为第i篇文档中词表中第i个词出现的概率,由于di
利用EM算法求
至此,我们就可以用em算法迭代求解了
其中、
需要用偏导数
=0求出
 180
180

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


