期货期权希腊字母与场景模拟

最新推荐文章于 2024-03-19 18:35:41 发布

ziyi_gong

最新推荐文章于 2024-03-19 18:35:41 发布

阅读量845

点赞数 1

分类专栏：金融工程-期权风险理论文章标签： SPAN保证金情景模拟期权风险 MATLAB 希腊字母

本文链接：https://blog.youkuaiyun.com/ziyi_gong/article/details/102486159

版权

金融工程-期权风险理论专栏收录该内容

1 篇文章

订阅专栏

@龚紫衣
期货期权风险不同于期货风险。期货价格和标的价格间居于线性关系。而期权价格和标的价格之间的关系是非线性的，假如我们知道期货价格的变动范围和期货期权的合约信息，可以发现期权价格并不随期货价格线性变动。如下所示：

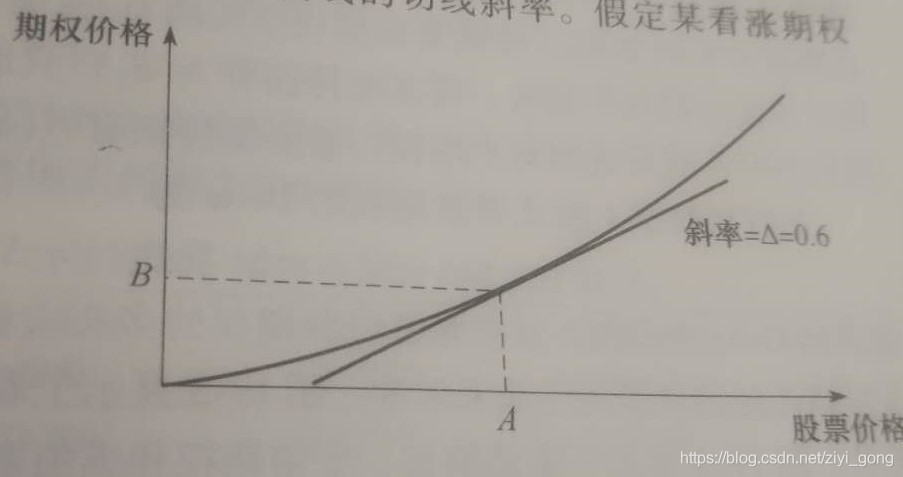且期权价格不仅仅和期货价格有关系，还和利率、执行价、到期时间、波动率有关。由于所有的风险都可以体现在价格上，针对上述四个维度与价格的关系，业界分别通过多个希腊字母来监控（含义请具体参考https://blog.youkuaiyun.com/lx0082002/article/details/100061696）。其中价格和波动率是最重要的两个影响因素。期权的风险往往通过场景模拟获得，场景的维度一般为价格和波动率。确定场景一般需要先获得：

当前价格
当前波动率
期货价格最大变动
波动率最大变动
价格最大变动倍数
波动率最大变动倍数
以CME-SPAN用到的场景设置为例（SPAN中的价格最最大变动称为PSR,波动率最大变动称为VSR，示例中对极端场景不分析，排除15和16）：

下面从Delta和Vega来推断单个期权合约最大风险可能会出的位置。
多看涨期权：由于当未来期权价格越低，多头方风险越大。看涨期权Delta>0,Vega>0，即期货期权价格和期货价格和波动率均成正比。因此在期货价格最低，波动率最小时风险最大，即场景14。
多看跌期权：由于当未来期权价格越低，多头方风险越大。看跌期权Delta<0,Vega>0，即期货期权价格和期货价格成反比，波动率成正比。因此在期货价格最高，波动率最小时风险最大，即场景12。
空看涨期权：由于当未来期权价格越高，空头方风险越大。看涨期权Delta>0,Vega>0，即期货期权价格和期货价格和波动率均成正比。因此在期货价格最高，波动率最高时风险最大，即场景11。
空看跌期权：由于当未来期权价格越高，空头方风险越大。看跌期权Delta<0,Vega>0，即期货期权价格和期货价格成反比，波动率成正比。因此在期货价格最低，波动率最大时风险最大，即场景13。

当有同一品种的多个期货期权构成组合时，对持有组合的最大风险场景是无法确定的。以无股息欧式期货期权为例,看涨的Delta近似为:N(d1)。看跌的Delta为N(d1)-1。假设投资组合由看涨期权多头和看跌期权多头构成，通MATLAB模拟可以得到组合的Delta的代码为（信息和公式都见代码）：

%  探索组合Delta与期货价格的关系
%  以多看涨期权1与多看跌期权2为例
sigma = 0.12; % 年化波动率
T1=0.35; T2=0.35; % 期权1和期权2的离到期时间
K1=6000; K2=5000; % 期权1和期权2的执行价
F=[4000:10:7000]; % 可能的期货价格
Nd11=normcdf((log(F/K1)+sigma^2*T1/2)/(sigma*sqrt(T1)));
% 期权1的Delta
Nd12=normcdf((log(F/K2)+sigma^2*T2/2)/(sigma*sqrt(T2)))-1;
Nd = Nd11+Nd12
% 期权2的Delta
plot(F,Nd11)
hold on
plot(F,Nd12)
hold on
plot(F,Nd)
legend('期权1','期权2','组合')
xlabel('期货价格')
ylabel('Delta')

所得图形为：
在这里插入图片描述
由于它的Delta值含有0以及两侧区间，无法轻易预测到风险最大的场景。所以它在CME-SPAN下每种场景下的价格均需要估计。例举仅为一种组合，在不同的组合情况下组合的Delta表现并不相同。且在估计时，仅考虑Delta因素，未考虑Vega因素。在综合考虑的情况下会更加复杂，这也是为何对期权组合未来价格估计使用场景模拟的原因之一。场景设置的密度越细，对风险考虑就会越周详。但在具体场景设计时需要对风险估计和效率进行权衡。