零基础上手扩散模型——一个新的理论视角_malldiffusion是什么-优快云博客

本文链接：https://blog.youkuaiyun.com/zhishi0000/article/details/144499695

文章题目：Diffusion models from scratch, from a new theoretical perspective
英文原文：https://www.chenyang.co/diffusion.html
ICML2024论文：https://proceedings.mlr.press/v235/permenter24a.html
代码：https://github.com/yuanchenyang/smalldiffusion

最近，扩散模型在生成模型领域取得了令人印象深刻的成果，特别是在从多模态分布中采样方面。扩散模型不仅在文生图（如Stable Diffusion）中得到了广泛采用，还在其他应用领域表现出色，例如音频/视频/3D生成、蛋白质设计、机器人路径规划，所有这些领域都需要从多模态分布中采样。

本教程旨在从优化的角度介绍扩散模型，这一视角首次在我们的论文中提出（与Frank Permenter合作）。本教程将涵盖理论和代码，使用理论来解释如何从零开始实现一个扩散模型。到本教程结束时，你将学会如何在一个toy数据集实现训练和采样，这些代码同样适用于更大的数据集和模型。

在本教程中，我们将主要参考malldiffusion。为了更加清晰，这里呈现的代码将从原始库中简化而来，原始代码本身有很好的注释并且易于阅读。

Training diffusion models

在这里插入图片描述
在实践中，通过以下简单的训练循环来完成：

def training_loop(loader  : DataLoader,
                  model   : nn.Module,
                  schedule: Schedule,
                  epochs  : int = 10000):
    optimizer = torch.optim.Adam(model.parameters())
    for _ in range(epochs):
        for x0 in loader:
            optimizer.zero_grad()
            sigma, eps = generate_train_sample(x0, schedule)
            eps_hat = model(x0 + sigma * eps, sigma)
            loss = nn.MSELoss()(eps_hat, eps)
            optimizer.backward(loss)
            optimizer.step()

训练循环遍历x0的批次，然后使用generate_train_sample函数采样噪声强度sigma和噪声向量eps：

def generate_train_sample(x0: torch.FloatTensor, schedule: Schedule):
    sigma = schedule.sample_batch(x0)
    eps = torch.randn_like(x0)
    return sigma, eps

Noise schedules

在这里插入图片描述

class Schedule:
    def __init__(self, sigmas: torch.FloatTensor):
        self.sigmas = sigmas
    def __getitem__(self, i) -> torch.FloatTensor:
        return self.sigmas[i]
    def __len__(self) -> int:
        return len(self.sigmas)
    def sample_batch(self, x0:torch.FloatTensor) -> torch.FloatTensor:
        return self[torch.randint(len(self), (x0.shape[0],))].to(x0)

在本教程中，我们将使用下面定义的log-linear schedule：

class ScheduleLogLinear(Schedule):
    def __init__(self, N: int, sigma_min: float=0.02, sigma_max: float=10):
        super().__init__(torch.logspace(math.log10(sigma_min), math.log10(sigma_max), N))

其他常用的schedule包括用于像素空间扩散模型的ScheduleDDPM和用于潜在扩散模型（如Stable Diffusion）的ScheduleLDM。下面的图表比较了这三种计划在默认参数下的情况。

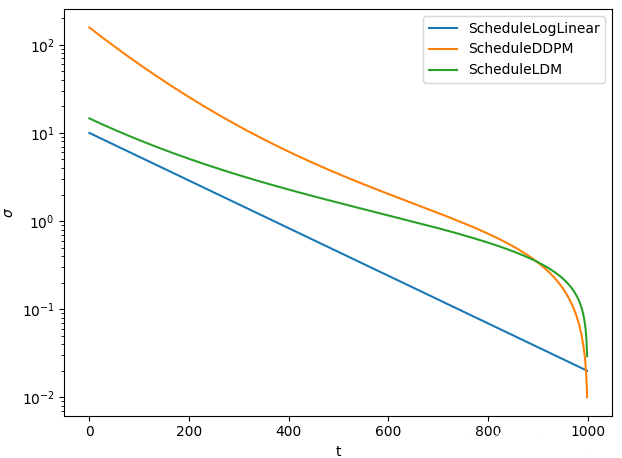
在这里插入图片描述
A comparison plot of different diffusion schedules

Toy example

在这里插入图片描述

dataset = Swissroll(np.pi/2, 5*np.pi, 100)
loader  = DataLoader(dataset, batch_size=2048)`

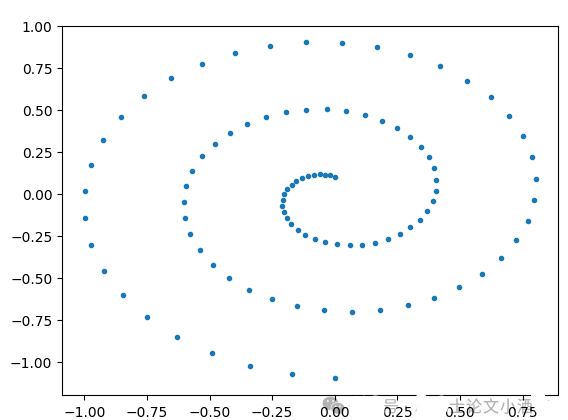
在这里插入图片描述
Swissroll toy dataset

对于这个简单的数据集，我们可以使用多层感知机（MLP）来实现去噪器：

def get_sigma_embeds(sigma):
    sigma = sigma.unsqueeze(1)
    return torch.cat([torch.sin(torch.log(sigma)/2),
                      torch.cos(torch.log(sigma)/2)], dim=1)

class TimeInputMLP(nn.Module):
    def __init__(self, dim, hidden_dims):
        super().__init__()
        layers = []
        for in_dim, out_dim in pairwise((dim + 2,) + hidden_dims):
            layers.extend([nn.Linear(in_dim, out_dim), nn.GELU()])
        layers.append(nn.Linear(hidden_dims[-1], dim))
        self.net = nn.Sequential(*layers)
        self.input_dims = (dim,)

    def rand_input(self, batchsize):
        return torch.randn((batchsize,) + self.input_dims)

    def forward(self, x, sigma):
        sigma_embeds = get_sigma_embeds(sigma)         # shape: b x 2
        nn_input = torch.cat([x, sigma_embeds], dim=1) # shape: b x (dim + 2)
        return self.net(nn_input)

model = TimeInputMLP(dim=2, hidden_dims=(16,128,128,128,128,16))

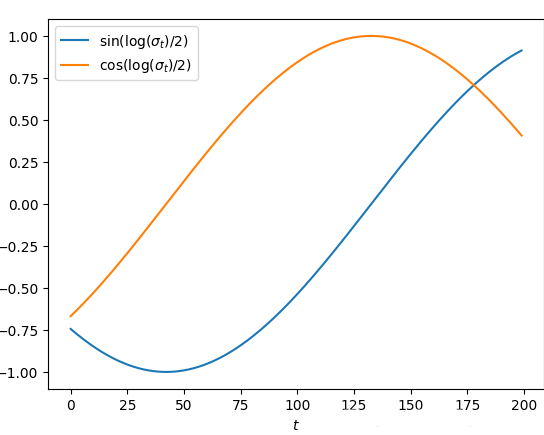
在这里插入图片描述
Two-dimensional embedding

现在我们有了训练扩散模型所需的所有要素。

schedule = ScheduleLogLinear(N=200, sigma_min=0.005, sigma_max=10)
trainer  = training_loop(loader, model, schedule, epochs=15000)
losses   = [ns.loss.item() for ns in trainer]

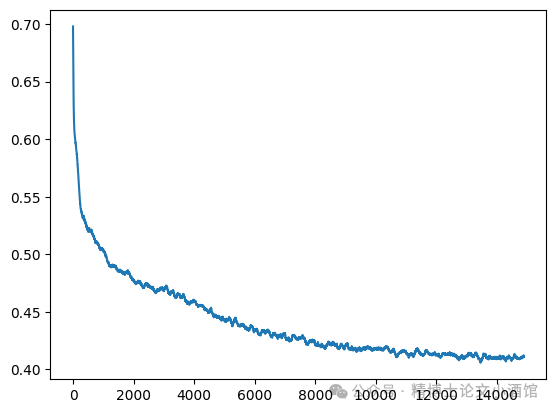
Training loss over 15000 epochs, smoothed with moving average

在这里插入图片描述

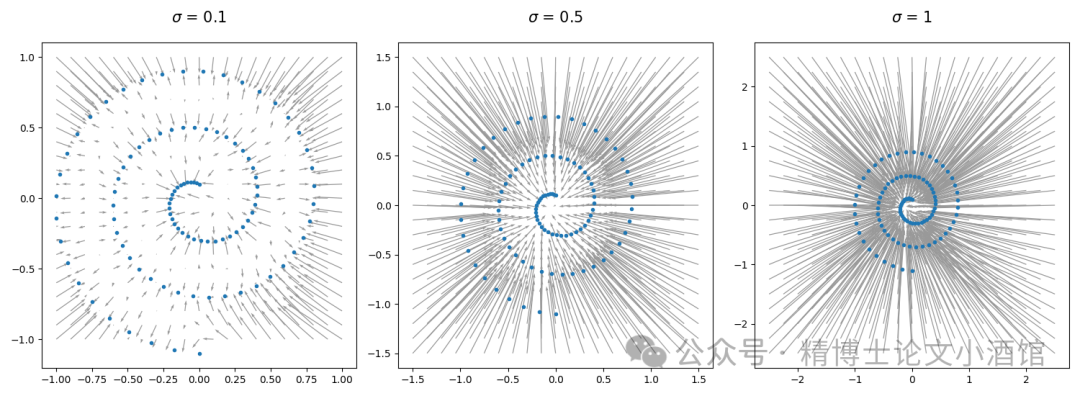Plot of predicted for differentand

在这里插入图片描述

Denoising as approximate projection

在这里插入图片描述

Distance and projection functions

在这里插入图片描述

下面的图片出自[Madan和Levin 2022]，展示了距离函数及其平滑版本的等高线。

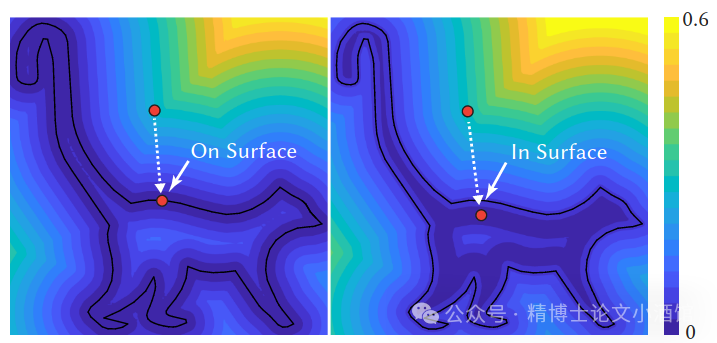Smoothed distance function has continuous gradients

在这里插入图片描述

Ideal denoiser

在这里插入图片描述

def sq_norm(M, k):
    # M: b x n --(norm)--> b --(repeat)--> b x k
    return (torch.norm(M, dim=1)**2).unsqueeze(1).repeat(1,k)

class IdealDenoiser:
    def __init__(self, dataset: torch.utils.data.Dataset):
        self.data = torch.stack(list(dataset))

    def __call__(self, x, sigma):
        x = x.flatten(start_dim=1)
        d = self.data.flatten(start_dim=1)
        xb, db = x.shape[0], d.shape[0]
        sq_diffs = sq_norm(x, db) + sq_norm(d, xb).T - 2 * x @ d.T
        weights = torch.nn.functional.softmax(-sq_diffs/2/sigma**2, dim=1)
        return (x - torch.einsum('ij,j...->i...', weights, self.data))/sigma

对于我们的toy数据集，我们可以绘制理想去噪器预测的不同噪声强度下的方向：

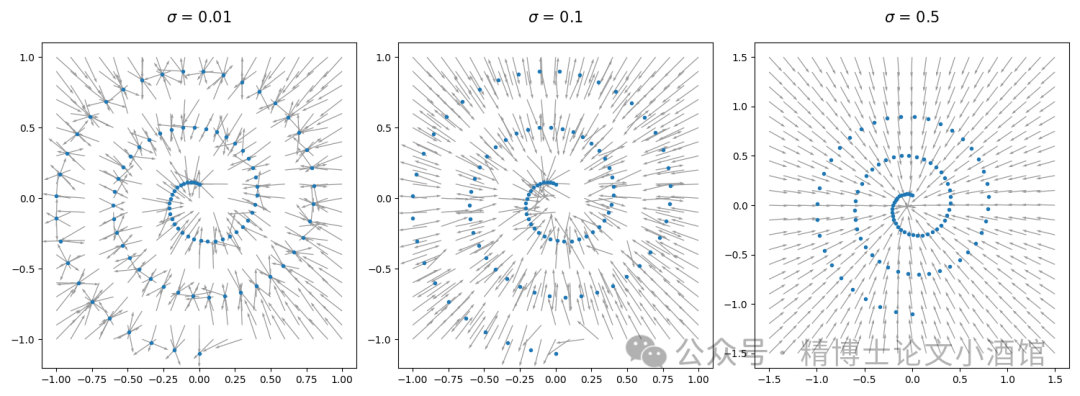Plot of direction of for different and

在这里插入图片描述

Relative error model

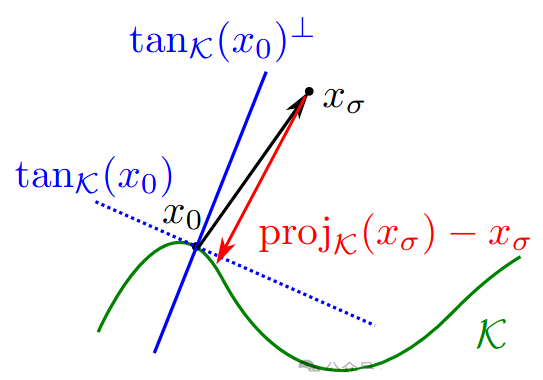
在这里插入图片描述

在这里插入图片描述
When added noise is small, most of noise is orthogonal to tangent space of manifold. Under the manifold hypothesis, denoising is approximately projection.

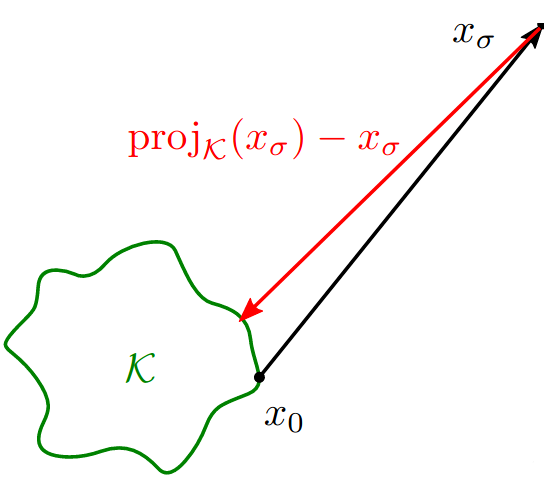
在这里插入图片描述

在这里插入图片描述
When added noise is large compared to diameter of data, denoising and projection point in the same direction

我们还对预训练的扩散模型在图像数据集上进行了我们误差模型的实证测试。CIFAR-10数据集足够小，可以方便地计算理想去噪器。我们的实验表明，对于这个数据集，精确投影和理想去噪器输出之间的相对误差在采样轨迹上是很小的。

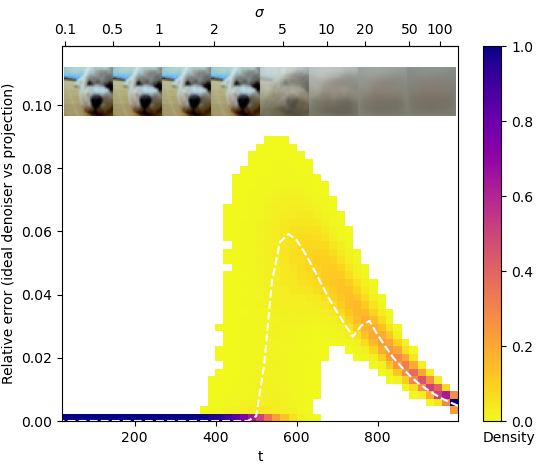
在这里插入图片描述
Ideal denoiser well-approximates projection onto the CIFAR-10 dataset under relative-error model

Sampling from diffusion models

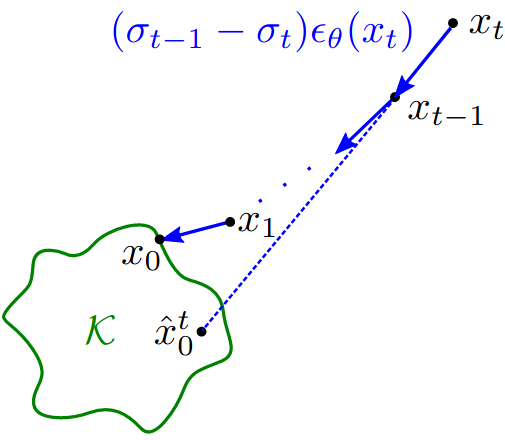
在这里插入图片描述

在这里插入图片描述
Sampling process iteratively calls the denoiser based on schedule.

在这里插入图片描述

Diffusion sampling as distance minimization

在这里插入图片描述

回到我们的示例，我们可以通过从原始的对数线性计划中进行子采样来找到一个可接受的计划，并如下实现DDIM采样器：

class Schedule:
    ...
    def sample_sigmas(self, steps: int) -> torch.FloatTensor:
        indices = list((len(self) * (1 - np.arange(0, steps)/steps))
                       .round().astype(np.int64) - 1)
        return self[indices + [0]]

batchsize = 2000
sigmas = schedule.sample_sigmas(20)
xt = model.rand_input(batchsize) * sigmas[0]
for sig, sig_prev in pairwise(sigmas):
    eps = model(xt, sig.to(xt))
    xt -= (sig - sig_prev) * eps

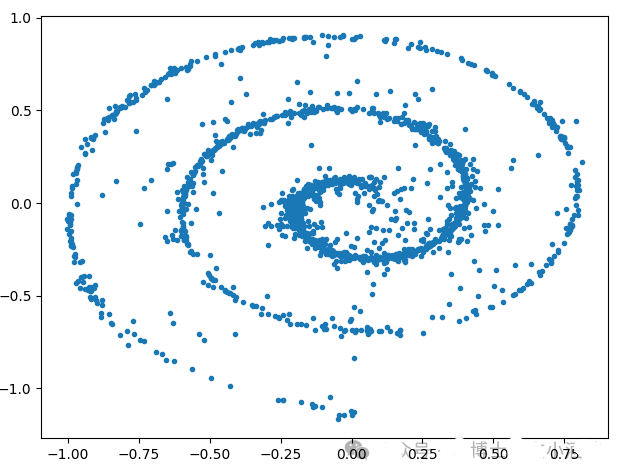
在这里插入图片描述
Samples from 20-step DDIM

我们观察到大多数样本都接近原始数据，但仍有改进的空间。一种方法是增加DDIM步骤的数量，但这会增加额外的计算成本。接下来，我们利用对扩散模型的解释来推导出一个更高效的采样器。

Improved sampler with gradient estimation

在这里插入图片描述

直观地说，这个更新使用当前估计来纠正前一步中产生的任何误差：

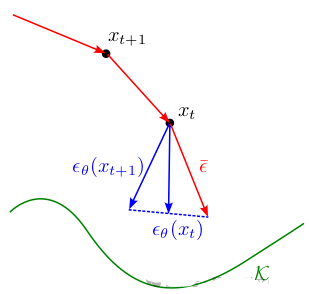
在这里插入图片描述
Our gradient estimation update step

与DDIM采样器相比，这导致更快的收敛，从我们的玩具模型上的样本更接近原始数据就可以看出。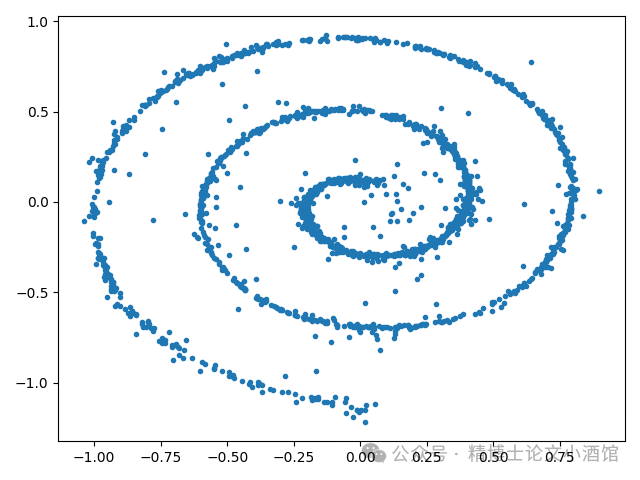

与默认的DDIM采样器相比，我们的采样器可以被解释为增加了动量，这可能会导致轨迹超调，但收敛速度更快。

Sampling trajectories varying momentum term

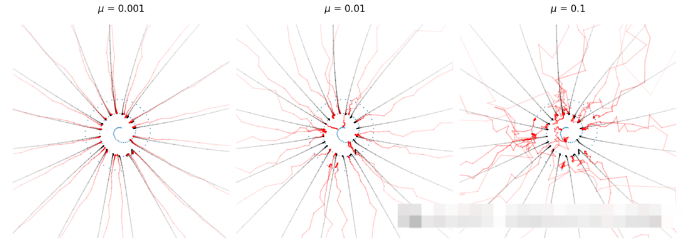
从经验上看，在生成过程中添加噪声也能提高采样质量。为了在坚持我们原始的计划的同时做到这一点，我们需要先对噪声强度在这里插入图片描述

在这里插入图片描述
Sampling trajectories varying amount of noise added during sampling

我们的梯度估计更新可以与采样过程中添加噪声结合起来。总之，我们的完整更新步骤是

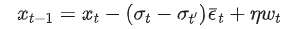
在这里插入图片描述

以下实现了一个全面的采样器，它概括了DDIM（gam=1,mu=0）、DDPM（gam=1,mu=0.5）和我们的梯度估计采样器（gam=2,mu=0）。

@torch.no_grad()
def samples(model      : nn.Module,
            sigmas     : torch.FloatTensor, # Iterable with N+1 values for N sampling steps
            gam        : float = 1.,        # Suggested to use gam >= 1
            mu         : float = 0.,        # Requires mu in [0, 1)
            xt         : Optional[torch.FloatTensor] = None,
            batchsize  : int = 1):
    xt = model.rand_input(batchsize) * sigmas[0]
    eps = None
    for i, (sig, sig_prev) in enumerate(pairwise(sigmas)):
        eps, eps_prev = model(xt, sig.to(xt)), eps
        eps_av = eps * gam + eps_prev * (1-gam)  if i > 0 else eps
        sig_p = (sig_prev/sig**mu)**(1/(1-mu)) # sig_prev == sig**mu sig_p**(1-mu)
        eta = (sig_prev**2 - sig_p**2).sqrt()
        xt = xt - (sig - sig_p) * eps_av + eta * model.rand_input(batchsize).to(xt)
        yield xt

Large-scale examples

上述训练代码不仅适用于我们的玩具数据集，还可以用于从头开始训练图像扩散模型。请参阅这个例子，了解如何在FashionMNIST数据集上训练，以在这个排行榜上获得第二名的FID得分：

Samples from a diffusion model trained on the FashionMNIST dataset

采样代码无需修改即可用于从最先进的预训练潜在扩散模型中采样：

schedule = ScheduleLDM(1000)
model    = ModelLatentDiffusion('stabilityai/stable-diffusion-2-1-base')
model.set_text_condition('An astronaut riding a horse')
*xts, x0 = samples(model, schedule.sample_sigmas(50))
decoded  = model.decode_latents(x0)

我们可以可视化我们的动量项在高分辨率文本到图像生成中的不同效果。

Text-to-image samples using Stable Diffusion

Other resources

同样推荐以下关于扩散模型的博客文章：

•What are diffusion models从离散时间角度介绍了扩散模型，即逆转马尔可夫过程。

•Generative modeling by estimating gradients of the data distribution从连续时间角度介绍了扩散模型，即逆转随机微分方程。

•The annotated diffusion model详细讲解了使用PyTorch实现扩散模型的过程。

Citation

@inproceedings{
permenter2024interpreting,
title={Interpreting and Improving Diffusion Models from an Optimization Perspective},
author={Frank Permenter and Chenyang Yuan},
booktitle={Forty-first International Conference on Machine Learning},
year={2024},
url={https://openreview.net/forum?id=o2ND9v0CeK}
}

如何学习大模型

现在社会上大模型越来越普及了，已经有很多人都想往这里面扎，但是却找不到适合的方法去学习。

作为一名资深码农，初入大模型时也吃了很多亏，踩了无数坑。现在我想把我的经验和知识分享给你们，帮助你们学习AI大模型，能够解决你们学习中的困难。

下面这些都是我当初辛苦整理和花钱购买的资料，现在我已将重要的AI大模型资料包括市面上AI大模型各大白皮书、AGI大模型系统学习路线、AI大模型视频教程、实战学习，等录播视频免费分享出来，需要的小伙伴可以扫取。

一、AGI大模型系统学习路线

很多人学习大模型的时候没有方向，东学一点西学一点，像只无头苍蝇乱撞，我下面分享的这个学习路线希望能够帮助到你们学习AI大模型。

在这里插入图片描述

二、AI大模型视频教程

在这里插入图片描述

三、AI大模型各大学习书籍

在这里插入图片描述

四、AI大模型各大场景实战案例

在这里插入图片描述

五、结束语

学习AI大模型是当前科技发展的趋势，它不仅能够为我们提供更多的机会和挑战，还能够让我们更好地理解和应用人工智能技术。通过学习AI大模型，我们可以深入了解深度学习、神经网络等核心概念，并将其应用于自然语言处理、计算机视觉、语音识别等领域。同时，掌握AI大模型还能够为我们的职业发展增添竞争力，成为未来技术领域的领导者。

再者，学习AI大模型也能为我们自己创造更多的价值，提供更多的岗位以及副业创收，让自己的生活更上一层楼。

因此，学习AI大模型是一项有前景且值得投入的时间和精力的重要选择。