前言(只说有用的干货,理清解算的思路)
在研究四轴飞行器的时候,一定会遇到姿态解算的问题,所谓的姿态解算,是从陀螺仪,加速度计等传感器中获得角速度,加速度等物理量,通过数学手段获得控制飞行器所需的三个欧拉角——分别是机头的上升与下降(俯仰角),机翼的左右偏转(横滚角),机头飞行的方向(偏航角)。
获得精确的角度是进行机体控制的前提,有关控制在下一篇文章。
1.机体坐标系与地面坐标系
机体坐标系一般情况下定义:
机头的方向为X轴正方向,机翼的右翼为Y轴正方向,机身原点竖直向下为Z轴正方向。
机体坐标系的作用有很多,但笔者认为主要有两条:
1.给陀螺仪,加速度计赋予真实的物理意义,陀螺仪和加速度计都是针对机体而测算的而不是地面。
2.机体坐标系与地面坐标系的偏差就是姿态角,后续的数学推导需要机体坐标系。
地面坐标系一般情况下定义:
正北为X轴正方向,正东为Y轴正方向,垂直与水平地面指向下为Z轴正方向,也就是重力的方向。
地面坐标系的作用主要是:
1.通过与机体坐标系对比,得出姿态角。是核心作用。
2.在更高级的带位置控制的无人机中,把无人机当成一个质点,地面坐标系可以给出位置信息。
机体坐标系与地面坐标系是理解后续内容的基础,要记住坐标系的方向。
2.四元数
为什么要用四元数? 因为四元数的本质是描述旋转
定义一个三维空间旋转的方式大概有三种,给出个表格特点如下:
| 特性 | 四元数 | 旋转矩阵 | 欧拉角 |
|---|---|---|---|
| 变量数量 | 4 | 9 | 3 |
| 计算效率 | 高(适合实时系统) | 低(矩阵乘法开销大) | 中(简单三角函数) |
| 奇点问题 | 无 | 无 | 有(万向节死锁) |
| 数值稳定性 | 需归一化 | 需正交化 | 误差易累积 |
| 物理意义 | 抽象(需转换理解) | 直观(坐标变换) | 直观(绕轴旋转) |
| 插值支持 | 优秀(SLERP) | 复杂(需Slerp或分解) | 差(非最优路径) |
| 典型应用场景 | IMU姿态估计、机器人控制 | 3D图形学、复杂变换 | 飞行仪表显示、用户交互 |
根据上面的特性,所以选择四元数。
这里引出四元数的定义:
在二维中,旋转可以用两个变量来表示:
q=cosθ+sinθ∗i
q = \cos \theta + \sin \theta * i
q=cosθ+sinθ∗i
则在三维旋转中,用四个变量来表示(由一个数学家发现,证明很复杂,不建议研究太深,作为工程师拿来用就好了):
q=q1+q2∗i+q3∗j+q4∗k
q= q1 +q2*i+q3*j+q4*k
q=q1+q2∗i+q3∗j+q4∗k
其中
q1=cosθ2q2=q3=q4=sinθ2
q1 = \cos \frac \theta 2 \\
q2 =q3=q4=\sin \frac \theta 2
q1=cos2θq2=q3=q4=sin2θ
这里的θ\thetaθ是在三维空间旋转的角度,i,j,ki,j,ki,j,k是单位向量。
划重点!便于后面的理解,这些定义要记住
q1q1q1是实部,也是标量部分。
q2,q3,q4q2,q3,q4q2,q3,q4是虚部系数。
i,j,ki,j,ki,j,k是虚数单位,并满足以下公式:
i2=j2=k2=ijk=−1ij=k,jk=i,ki=jji=−k,kj=−i,ik=−j
i^2=j^2=k^2=ijk=-1 \\
ij=k,jk=i,ki=j \\
ji=-k,kj=-i,ik=-j
i2=j2=k2=ijk=−1ij=k,jk=i,ki=jji=−k,kj=−i,ik=−j
总结并很重要:按照i,j,ki,j,ki,j,k的顺序,顺序相乘为正,逆序相乘为负。
3.四元数微分方程
1. 数学定义
设:
- q=[q0,q1,q2,q3]T\mathbf{q} = [q_0, q_1, q_2, q_3]^Tq=[q0,q1,q2,q3]T 为单位四元数(q02+q12+q22+q32=1q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1q02+q12+q22+q32=1)
- ω=[ωx,ωy,ωz]T\boldsymbol{\omega} = [\omega_x, \omega_y, \omega_z]^Tω=[ωx,ωy,ωz]T 为刚体的角速度向量(单位:rad/s)
则四元数的微分方程为:
q˙=12q⊗Ω
\dot{\mathbf{q}} = \frac{1}{2} \mathbf{q} \otimes \boldsymbol{\Omega}
q˙=21q⊗Ω
其中:
- Ω=[0−ωx−ωy−ωzωx0ωz−ωyωy−ωz0ωxωzωy−ωx0]\boldsymbol{\Omega} = \begin{bmatrix} 0 & -\omega_x & -\omega_y & -\omega_z \\ \omega_x & 0 & \omega_z & -\omega_y \\ \omega_y & -\omega_z & 0 & \omega_x \\ \omega_z & \omega_y & -\omega_x & 0 \end{bmatrix}Ω=⎣⎢⎢⎡0ωxωyωz−ωx0−ωzωy−ωyωz0−ωx−ωz−ωyωx0⎦⎥⎥⎤ 为角速度对应的斜对称矩阵
- ⊗\otimes⊗ 表示四元数乘法
展开后得到分量形式:
{q˙0=−12(ωxq1+ωyq2+ωzq3)q˙1=12(ωxq0−ωyq3+ωzq2)q˙2=12(ωyq0−ωzq1+ωxq3)q˙3=12(ωzq0−ωxq2+ωyq1)
\begin{cases}
\dot{q}_0 = -\frac{1}{2} (\omega_x q_1 + \omega_y q_2 + \omega_z q_3) \\
\dot{q}_1 = \frac{1}{2} ( \omega_x q_0 - \omega_y q_3 + \omega_z q_2 ) \\
\dot{q}_2 = \frac{1}{2} ( \omega_y q_0 - \omega_z q_1 + \omega_x q_3 ) \\
\dot{q}_3 = \frac{1}{2} ( \omega_z q_0 - \omega_x q_2 + \omega_y q_1 )
\end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧q˙0=−21(ωxq1+ωyq2+ωzq3)q˙1=21(ωxq0−ωyq3+ωzq2)q˙2=21(ωyq0−ωzq1+ωxq3)q˙3=21(ωzq0−ωxq2+ωyq1)
上述推导过程本质是向量q\mathbf{q}q和向量ω\boldsymbol{\omega}ω的叉乘运算,这里的Ω\boldsymbol{\Omega}Ω是为了方便运算直接给出的,但根本的运算逻辑是q\mathbf{q}q和ω=[0,ωx,ωy,ωz]T\boldsymbol{\omega} = [0, \omega_x, \omega_y, \omega_z]^Tω=[0,ωx,ωy,ωz]T的叉乘,计算过程很复杂,这里给出计算过程,不想看的可以跳过,直接记结论。
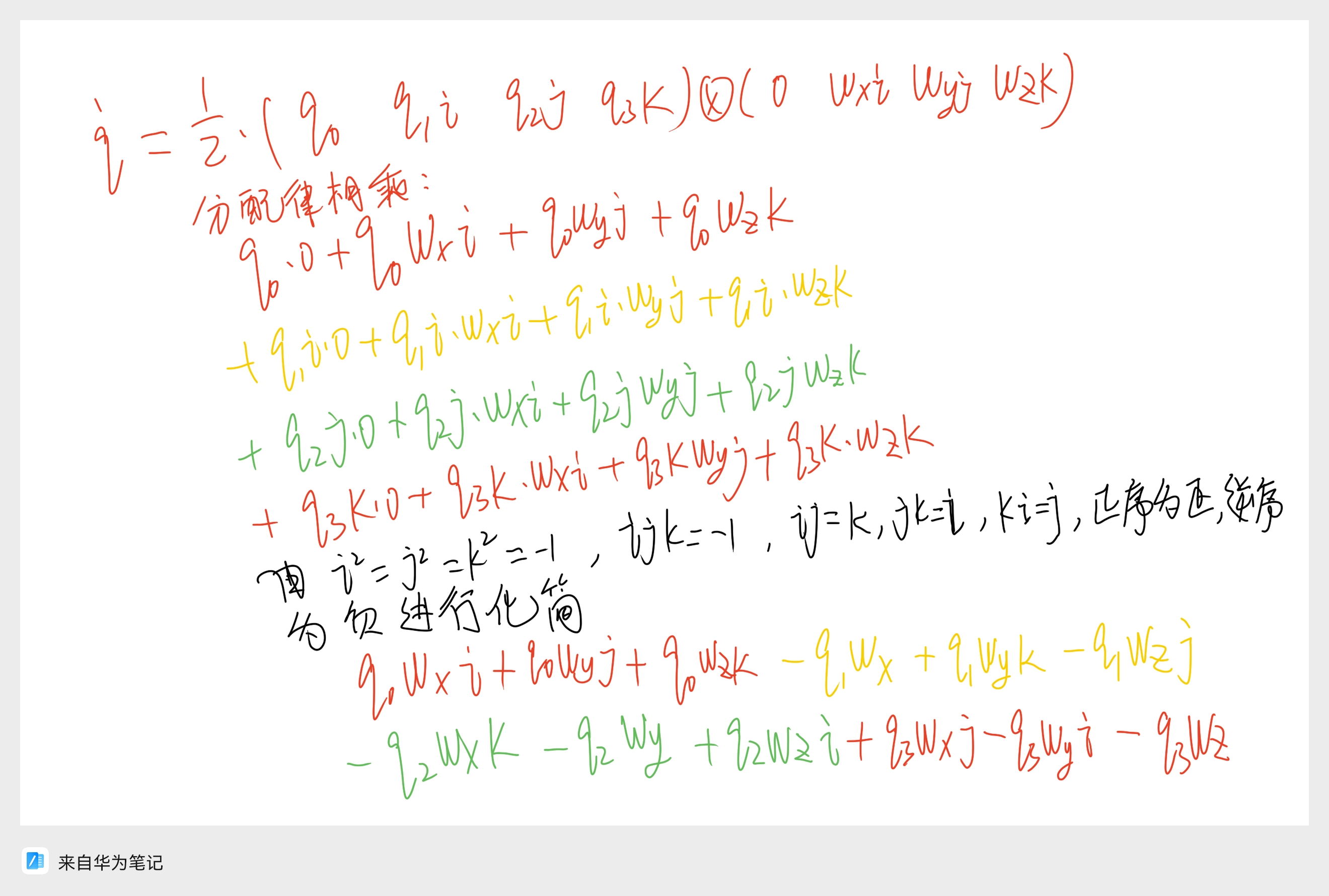

有了四元数,为什么要四元数微分方程?
因为四元数描述的是一个静态旋转量,通俗来讲就是三维向量围绕哪个轴旋转了多少度,告诉了我们此刻这个三维向量的旋转信息,而微分方程描述的是动态的旋转过程,动态的旋转在时间的作用下变成了静态的旋转量。
从物理的角度来讲,四元数的变量是角度,角度的微分是角速度。微分方程的变量是角速度,所以角速度的改变(来自陀螺仪的数据)通过微分方程的计算得到四元数的导数,在进行积分得到更新后的四元数。
4.旋转矩阵
有了四元数和微分方程,我们就能通过陀螺仪提供的角速度信息,代入微分方程计算出更新后的四元数,四元数里包含着旋转后的角度信息,但是如何从四元数里得到我们想要的欧拉角,答案藏在旋转矩阵里。
旋转矩阵的物理意义
旋转矩阵 R 是坐标系变换算子,其物理意义如下:
向量变换公式
vworld=R⋅vbody\mathbf{v}_{world} = \mathbf{R} \cdot \mathbf{v}_{body}vworld=R⋅vbody
- 列向量:表示世界坐标系各轴在机体坐标系中的投影方向
- 行向量:表示机体坐标系各轴在世界坐标系中的投影方向
从四元数推导旋转矩阵
通过四元数旋转公式:
v′=q⊗v⊗q∗\mathbf{v}' = \mathbf{q} \otimes \mathbf{v} \otimes \mathbf{q}^*v′=q⊗v⊗q∗
展开后得到旋转矩阵 R 的具体形式:
R=[1−2(q22+q32)2(q1q2−q0q3)2(q1q3+q0q2)2(q1q2+q0q3)1−2(q12+q32)2(q2q3−q0q1)2(q1q3−q0q2)2(q2q3+q0q1)1−2(q12+q22)]
\mathbf{R} = \begin{bmatrix}
1-2(q_2^2+q_3^2) & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2) \\
2(q_1q_2+q_0q_3) & 1-2(q_1^2+q_3^2) & 2(q_2q_3-q_0q_1) \\
2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & 1-2(q_1^2+q_2^2)
\end{bmatrix}
R=⎣⎡1−2(q22+q32)2(q1q2+q0q3)2(q1q3−q0q2)2(q1q2−q0q3)1−2(q12+q32)2(q2q3+q0q1)2(q1q3+q0q2)2(q2q3−q0q1)1−2(q12+q22)⎦⎤
这里针对旋转矩阵 R 的推导过程给出部分手算过程,本质也是向量叉乘计算。

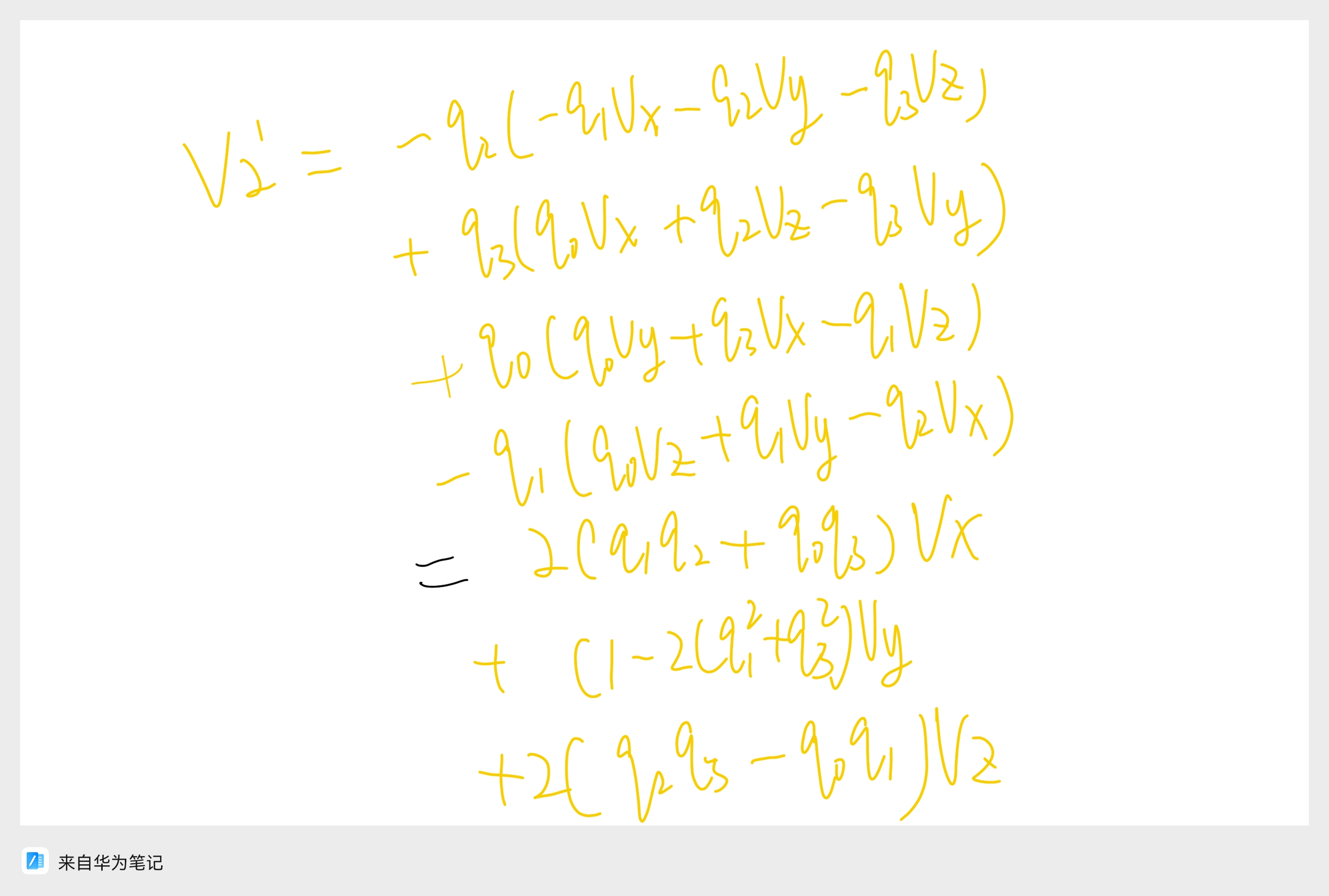
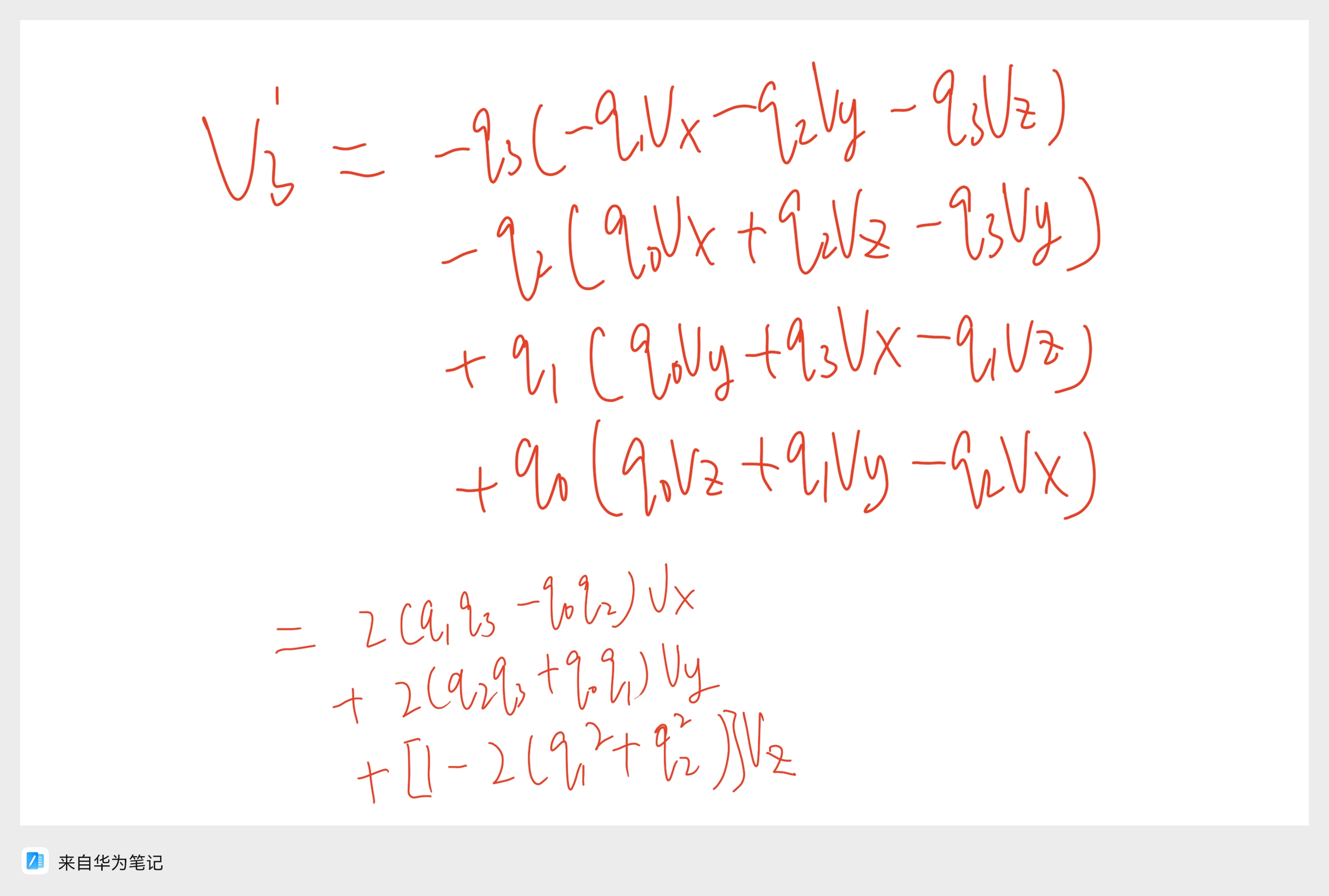
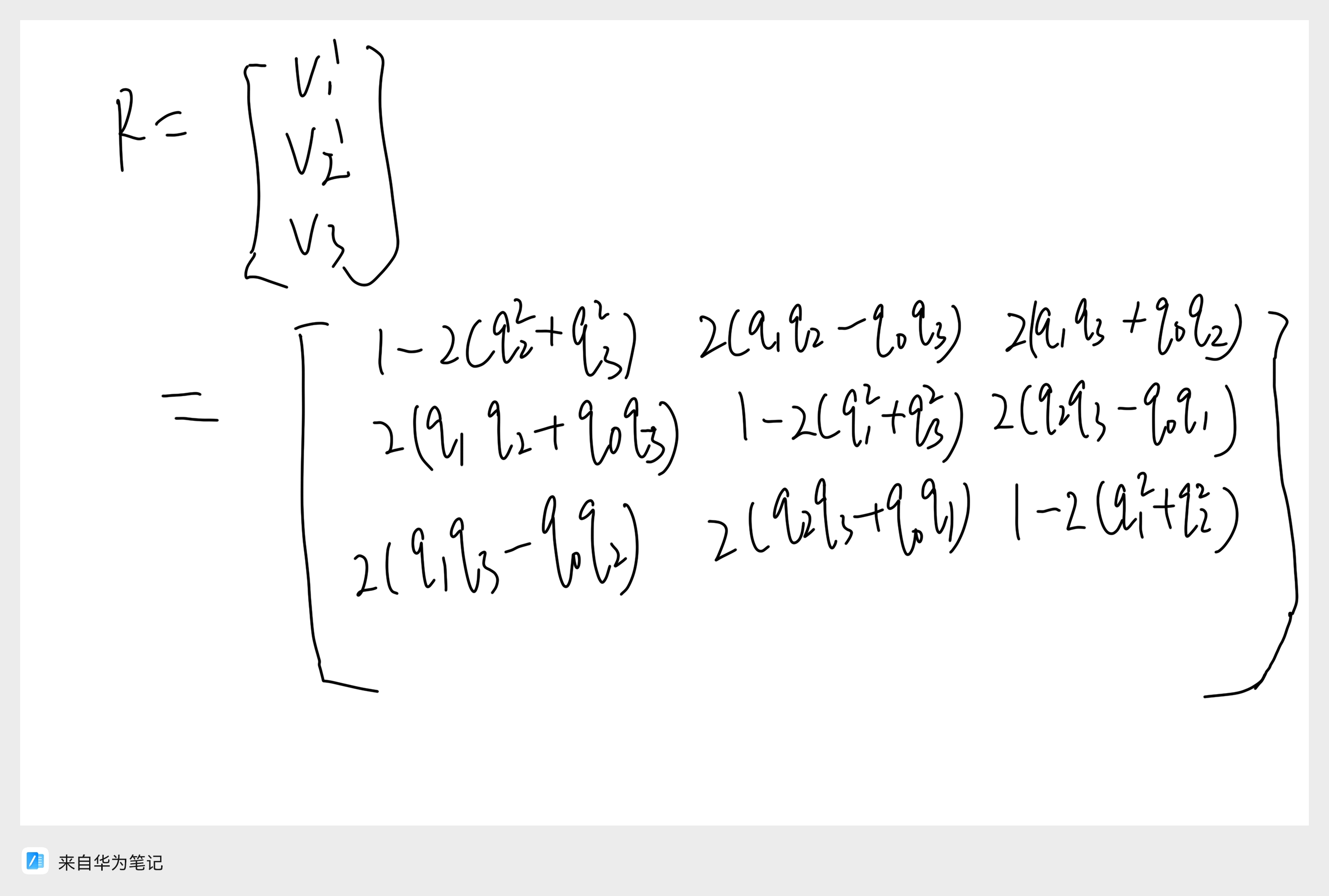
5.欧拉角
有了旋转矩阵,如何得到欧拉角?答案如下:
欧拉角是从旋转矩阵中通过数学反解推导得出的,其核心在于根据旋转顺序分解矩阵元素并应用反三角函数。以下是完整的原理和推导过程:
一、基本原理与关键约束
-
旋转矩阵的数学本质
旋转矩阵 RRR 是正交矩阵(R−1=RTR^{-1} = R^TR−1=RT),其行列式为1。欧拉角通过三个连续绕轴旋转(如Z-Y-X)合成该矩阵:
R=Rz(ψ)Ry(θ)Rx(ϕ) R = R_z(\psi) R_y(\theta) R_x(\phi) R=Rz(ψ)Ry(θ)Rx(ϕ)
其中 ψ,θ,ϕ\psi, \theta, \phiψ,θ,ϕ 分别为偏航角(yaw)、俯仰角(pitch)、横滚角(roll)。 -
旋转顺序的重要性
不同旋转顺序对应不同的矩阵分解形式(如XYZ、ZYX、YXZ)。以最常见的 ZYX顺序(航空航天领域标准)为例:- 先绕Z轴旋转 ψ\psiψ → Rz(ψ)R_z(\psi)Rz(ψ)
- 再绕Y轴旋转 θ\thetaθ → Ry(θ)R_y(\theta)Ry(θ)
- 最后绕X轴旋转 ϕ\phiϕ → Rx(ϕ)R_x(\phi)Rx(ϕ)。
二、ZYX顺序的详细推导
设旋转矩阵为:
R=[r11r12r13r21r22r23r31r32r33] R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} R=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤
步骤1:展开合成矩阵
通过矩阵乘法展开 R=Rz(ψ)Ry(θ)Rx(ϕ)R = R_z(\psi) R_y(\theta) R_x(\phi)R=Rz(ψ)Ry(θ)Rx(ϕ),得到元素表达式:
r11=cosψcosθr21=sinψcosθr31=−sinθr32=cosθsinϕr33=cosθcosϕ
\begin{aligned}
r_{11} &= \cos\psi \cos\theta \\
r_{21} &= \sin\psi \cos\theta \\
r_{31} &= -\sin\theta \\
r_{32} &= \cos\theta \sin\phi \\
r_{33} &= \cos\theta \cos\phi
\end{aligned}
r11r21r31r32r33=cosψcosθ=sinψcosθ=−sinθ=cosθsinϕ=cosθcosϕ
步骤2:反解欧拉角
-
俯仰角 θ\thetaθ(绕Y轴)
由 r31=−sinθr_{31} = -\sin\thetar31=−sinθ 直接得:
θ=arcsin(−r31) \theta = \arcsin(-r_{31}) θ=arcsin(−r31) -
偏航角 ψ\psiψ(绕Z轴)
由 r11=cosψcosθr_{11} = \cos\psi \cos\thetar11=cosψcosθ 和 r21=sinψcosθr_{21} = \sin\psi \cos\thetar21=sinψcosθ 得:
ψ=atan2(r21,r11) \psi = \mathrm{atan2}(r_{21}, r_{11}) ψ=atan2(r21,r11)
(atan2\mathrm{atan2}atan2 是四象限反正切函数,解决符号歧义) -
横滚角 ϕ\phiϕ(绕X轴)
由 r32=cosθsinϕr_{32} = \cos\theta \sin\phir32=cosθsinϕ 和 r33=cosθcosϕr_{33} = \cos\theta \cos\phir33=cosθcosϕ 得:
ϕ=atan2(r32,r33) \phi = \mathrm{atan2}(r_{32}, r_{33}) ϕ=atan2(r32,r33)
展开合成矩阵这一步是省略的,本人给出完整计算过程!
这里的思路是绕不同轴的四元数不同,代入四元数到上一步的旋转矩阵里,可以得到单独绕不同轴的旋转矩阵 Rx,Ry,Rz。
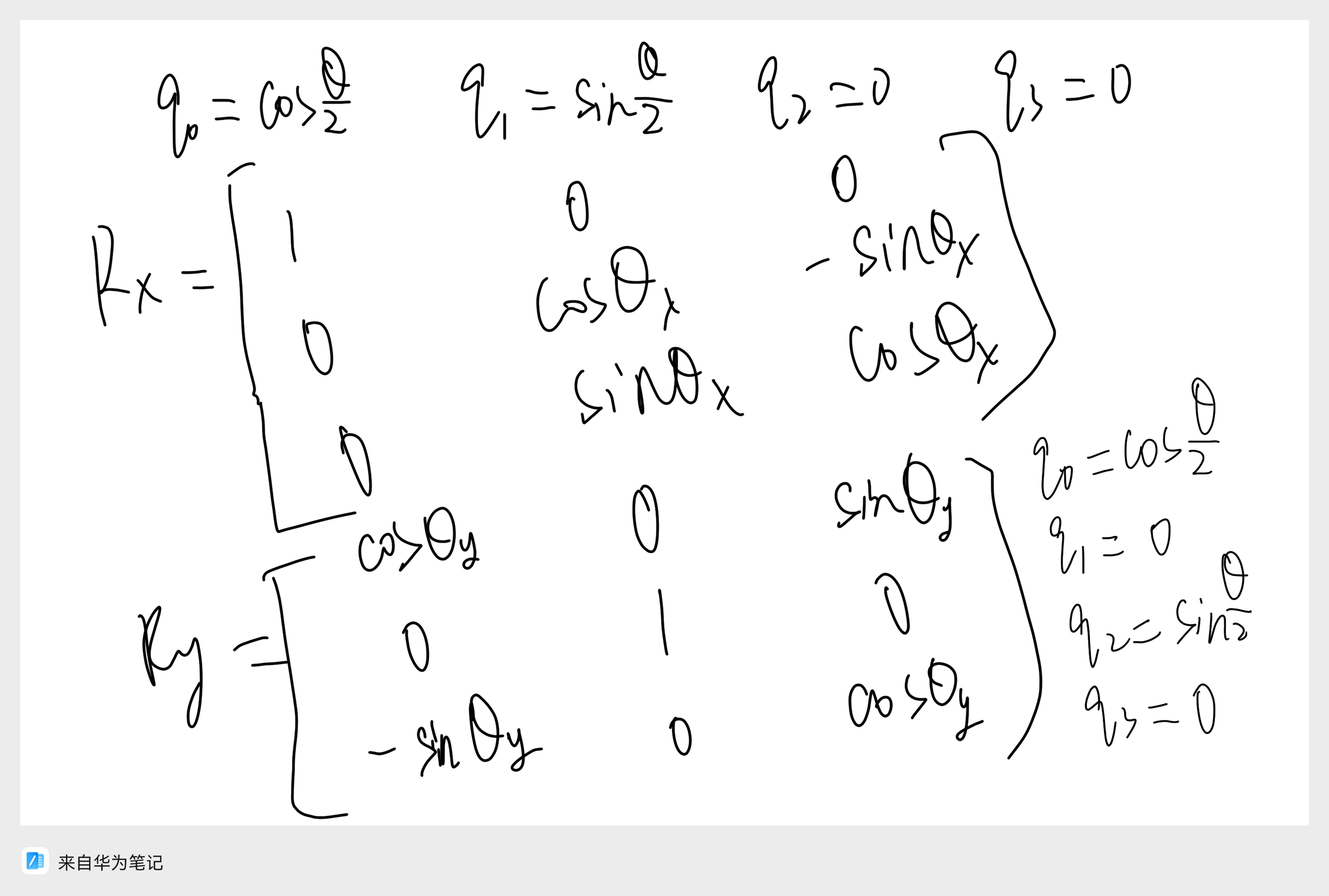
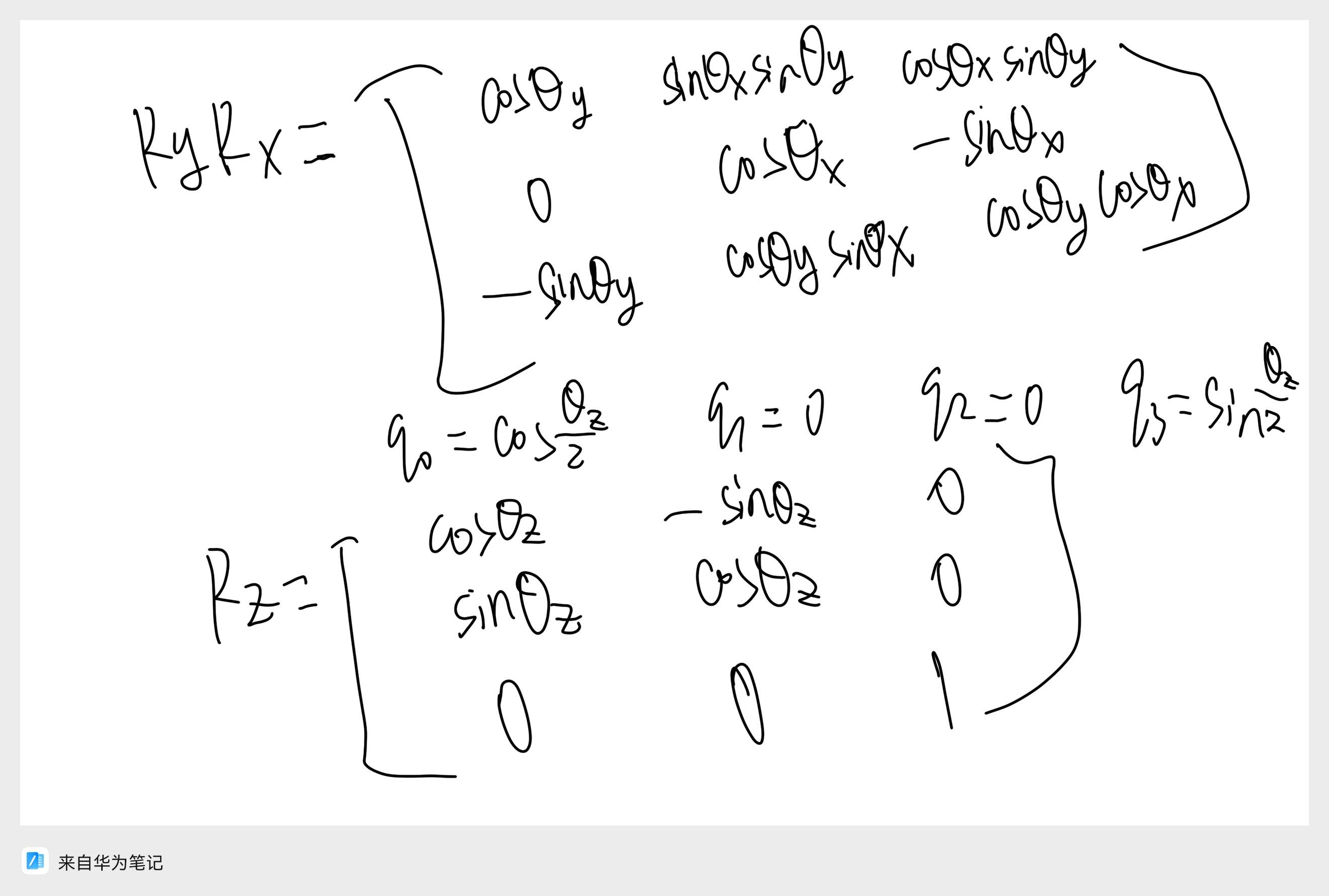

数值计算示例(绕Z轴旋转90°)
给定旋转矩阵(ZYX顺序):
R=[0−10100001] R = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} R=⎣⎡010−100001⎦⎤
- 计算俯仰角 θ\thetaθ:
θ=arcsin(−r31)=arcsin(−0)=0∘\theta = \arcsin(-r_{31}) = \arcsin(-0) = 0^\circθ=arcsin(−r31)=arcsin(−0)=0∘ - 计算偏航角 ψ\psiψ:
ψ=atan2(r21,r11)=atan2(1,0)=90∘\psi = \mathrm{atan2}(r_{21}, r_{11}) = \mathrm{atan2}(1, 0) = 90^\circψ=atan2(r21,r11)=atan2(1,0)=90∘ - 计算横滚角 ϕ\phiϕ:
ϕ=atan2(r32,r33)=atan2(0,1)=0∘\phi = \mathrm{atan2}(r_{32}, r_{33}) = \mathrm{atan2}(0, 1) = 0^\circϕ=atan2(r32,r33)=atan2(0,1)=0∘
结果符合绕Z轴旋转90°的预期。
由此,我们通过旋转矩阵解算出了欧拉角。
6.互补滤波
写到此处,有一个疑问相信有一部分人存在,那就是既然我们已经知道了角速度,为什么不用角速度直接积分,就是角度呢。当时的我也存在这个疑问,直到自己亲自动手实验才发现,刚才的想法,理论上是正确的,但现实是骨感的。
陀螺仪存在零点漂移!,而且非常严重,随着时间的增加,这个漂移的角度几分钟就可以偏差几度,甚至十几度,属于是完全不能用的存在。有条件的同学可以实践一下,如下图是本人的实践效果:
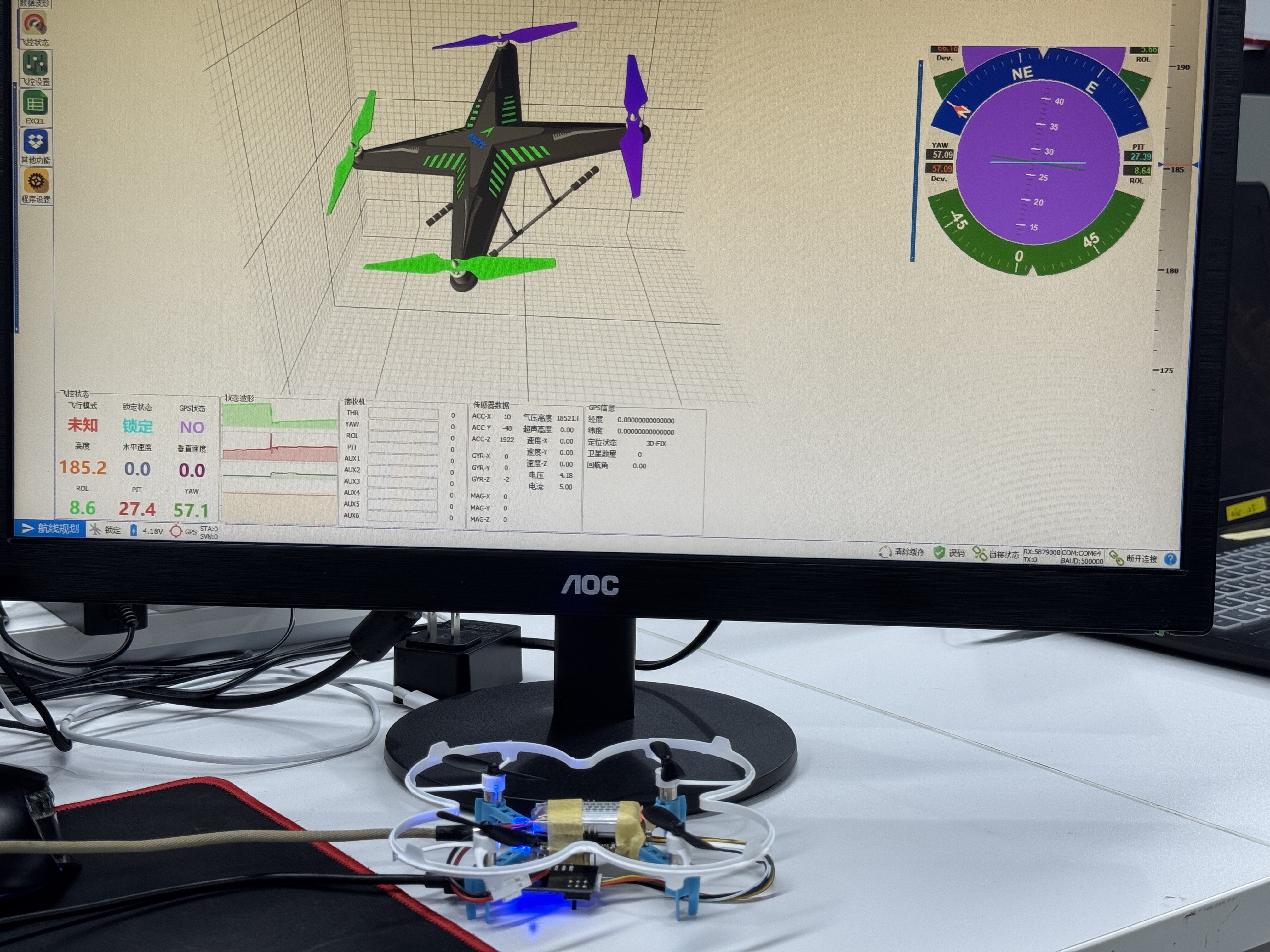


























 7832
7832

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










