Factorization Machines（FM）：发展过程、原理及实现

原创已于 2022-08-17 12:00:16 修改 · 994 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#python #推荐算法

于 2022-08-17 11:58:13 首次发布

推荐系统基础学习笔记专栏收录该内容

15 篇文章

订阅专栏

本文详细介绍了从逻辑回归（LR）到POLY2模型，再到矩阵分解（MF）的演变，最终引出了因子化机（FM）模型。FM模型结合了POLY2的特征交叉和MF的低维表示，有效解决了稀疏数据下的特征组合问题，并保持了线性预测复杂度。文章还给出了FM模型的代码实现，展示了如何构建FM模型的一阶和二阶特征，并总结了FM模型的优势和优化点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、前言

FM主要是解决稀疏数据下的特征组合问题，并且其预测的复杂度是线性的，对于连续和离散特征有较好的通用性。

下面就从它的发展由来：

1、逻辑回归模型（LR）

前面提到逻辑回归模型已经可以把用户特征，商品特征以及上下文特征进行了利用，

但是逻辑回归存在很大的一个问题就是只对单一特征做简单加权，不具备特征交叉生成组合特征的能力，LR的公式如下：

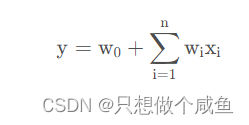
进而发展出可以进行特征组合的POLY2模型

2、POLY2模型

POLY2模型进行特征的“暴力”组合就成了可行的选择。 POLY2 数学形式如下：

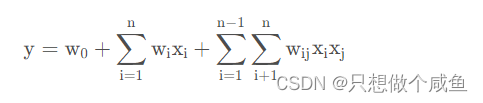
我们可以看到该模型将所有的特征进行两两交叉，并对所有的特征组合赋予权重权重W，我们可以看到相比于逻辑回归模型就是多了特征的两两组合

这样的模型存在缺点：

( 1 ) 在处理互联网数据时，经常采用 one-hot 编码的方法处理类别型数据，致使特征向量极度稀疏，POLY2 进行无选择的特征交叉—原本就非常稀疏的特征向量更加稀疏，导致大部分交叉特征的权重缺乏有效的数据进行训练，无法收敛。

( 2 ) 权重参数的数量上升 , 极大地增加了训练复杂度。

3、MF模型

矩阵分解（MF）：MATRIXFACTORIZATIONTECHNIQUES FORRECOMMENDERSYSTEMS_只想做个咸鱼的博客-优快云博客

这个模型前面有细致的讲解，可以回看，MF的核心思想就是生成用户和物品的隐向量通过内积的形式来表示共现矩阵。

随之而来的就是FM的铺垫结束，也就是POLY2模型+MF的思想进行了组合造就了FM模型的出现

二、FM（Factorization Machines）模型

上面提到，POLY2可以进行特征组合，缺点是每个特征组合都有权重W训练起来参数太多，MF可以将矩阵拆解成两个矩阵的内积形式，如果将POLY2的权重W都给拆了，这样就可以大幅减少训练的参数数量，同时也可以解决稀疏性的问题。

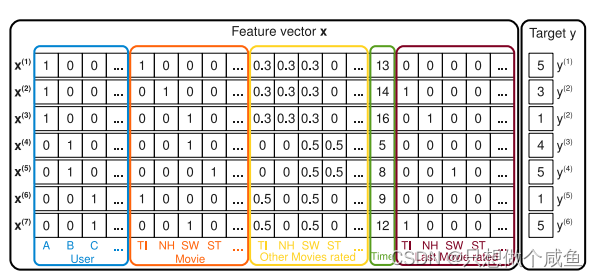
每行表示目标 y(i) 与其对应的特征向量 x(i) ，蓝色区域表示了用户变量，红色区域表示了电影变量，黄色区域表示了其他隐含的变量，进行了归一化，绿色区域表示一个月内的投票时间，棕色区域表示了用户上一个评分的电影，最右边的区域是评分。

有了这样的一个铺垫，就可以写出FM的模型方程了，就是POLY2 的基础上，把权重矩阵W拆解，写成了两个隐向量相乘的方式。数学公式表示如下：

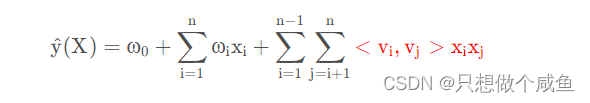
三、代码实现

# FM 特征组合层
class crossLayer(layers.Layer):
    def __init__(self, input_dim, output_dim=10, **kwargs):
        super(crossLayer, self).__init__(**kwargs)
        
        self.input_dim = input_dim
        self.output_dim = output_dim
        
        # 定义交叉特征的权重
        self.kernel = self.add_weight(name='kernel', shape=(self.input_dim, self.output_dim), initializer='glorot_uniform', trainable=True)
    
    def call(self, x): # 对照上述公式中的二次项优化公式理解
        a = K.pow(K.dot(x, self.kernel), 2)
        b = K.dot(K.pow(x, 2), K.pow(self.kernel, 2))
        return 0.5 * K.mean(a-b, 1, keepdims=True)
    
# 定义FM模型
def FM(feature_dim):
    inputs = Input(shape=(feature_dim, ))
    
    # 一阶特征
    linear = Dense(units=1, kernel_regularizer=regularizers.l2(0.01), bias_regularizer=regularizers.l2(0.01))(inputs)
    
    # 二阶特征
    cross = crossLayer(feature_dim)(inputs)
    add = Add()([linear, cross])            # 将一阶特征与二阶特征相加构建FM模型
    
    pred = Activation('sigmoid')(add)
    model = Model(inputs=inputs, outputs=pred)
    
    model.compile(loss='binary_crossentropy', optimizer=optimizers.Adam(), metrics=['binary_accuracy'])
    
    return model