目录
前言:
经过了一周的反复学习,将排序这一部分学完了,在程序设计中,排序的重要性无与伦比,下面,我就给大家分享排序算法这一部分的内容,让大家从0到1学会排序算法。结尾附可运行的完整代码,供大家参考。
一、排序的概念及运用
1.概念:
排序:所谓排序,就是使⼀串记录,按照其中的某个或某些关键字的⼤小,递增或递减的排列起来的操作。
2.运用:
排序算法的运用非常广泛,比如常见的有:购物筛选排序、高校排名等等。
3.常见的排序算法:
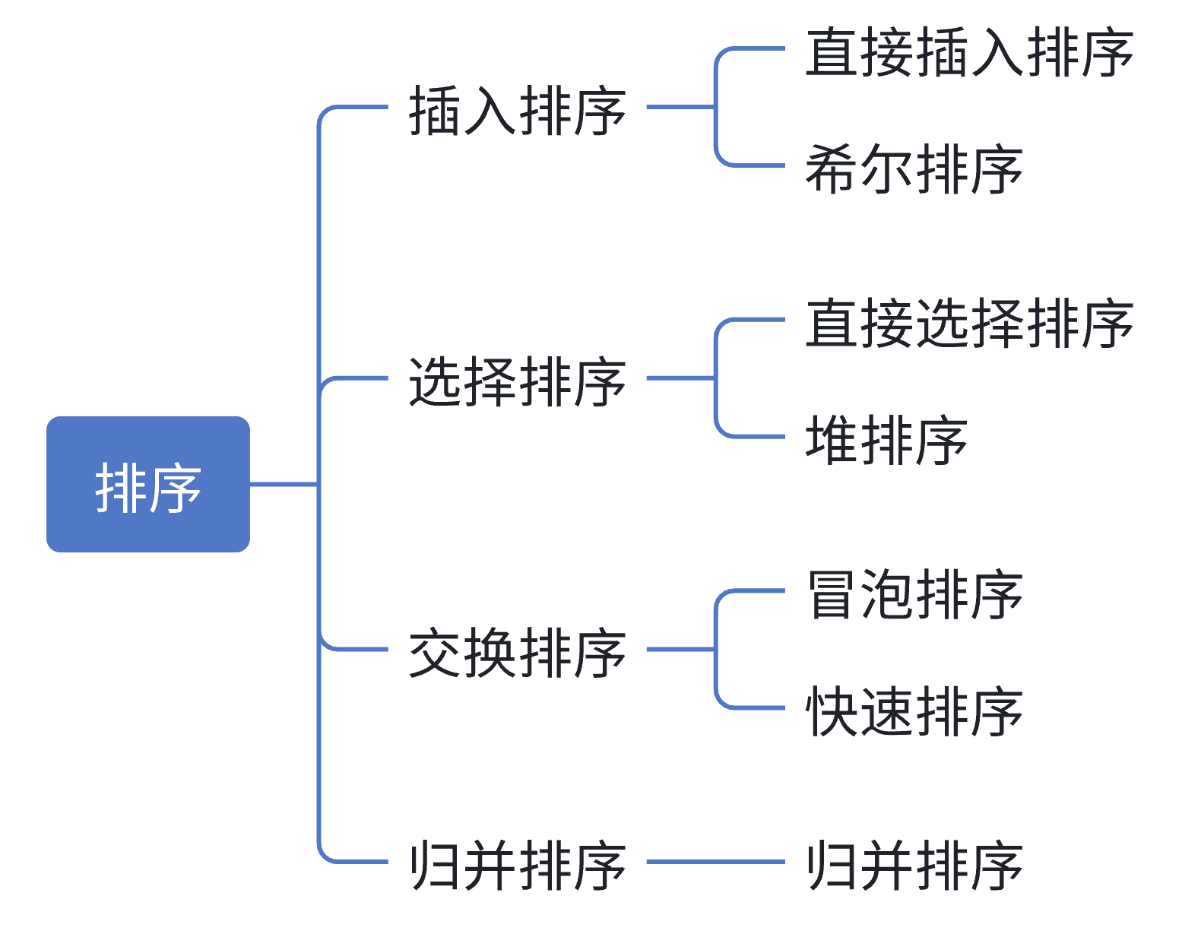
二、代码实现常见的排序算法
1.插入排序
1)直接插入排序:
直接插入排序是将待排序的数据按其关键码值的大小逐个插入到⼀个已经排好序的有序序列中,直到所有的数据插⼊完为止,从而得到⼀个新的有序序列 。
实现思路:
当插⼊第 i(i>=1) 个元素时,前⾯的 array[0],array[1],…,array[i-1] 已经排好序,此时⽤ array[i] 的排序码与 array[i-1],array[i-2],… 的排序码顺序进⾏⽐较,找到插⼊位置即将 array[i] 插⼊,原来位置上的元素顺序后移。
代码实现:
//1)直接插入排序
void InsertSort(int* arr, int n)
{
for (int i = 0;i < n - 1;i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else {
break;
}
}
arr[end + 1] = tmp;
}
}直接插⼊排序的特性总结
1. 元素集合越接近有序,直接插⼊排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
2)希尔排序:
希尔排序法又称缩小增量法。希尔排序是在直接插入排序算法的基础上进行改进⽽来的,综合来说它的效率肯定是要高于直接插⼊排序算法的。
实现思路:
先选定⼀个整数(通常是gap = n/3+1),把待排序⽂件所有记录分成各组,所有的距离相等的记录分在同⼀组内,并对每⼀组内的记录进⾏排序,然后gap=gap/3+1得到下⼀个整数,再将数组分成各组,进⾏插⼊排序,当gap=1时,就相当于直接插⼊排序。
代码实现:
//2)希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0;i < n - gap;i++)//将数据分成gap组,每组进行预排序(i++是依次对每组的数据进行排序)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else {
break;
}
}
arr[end + gap] = tmp;
}
}
}希尔排序的特性总结
1. 希尔排序是对直接插入排序的优化。
2. 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当 gap == 1 时,数组已经接近有序的了,这样就会很快。这样整体⽽⾔,可以达到优化的效果。
3. 时间复杂度:O(nlogn) ~ O(n^2),我们认为其为O(n^1.3)。由于希尔排序的时间复杂度计算非常困难,大家感兴趣的可以自行查询。
2.选择排序
1)直接选择排序:
直接选择排序就是直接在该数组中找最大值和最小值,分别将最大值和最小值分别放到序列的尾部和头部,循环直到全部放完。
实现思路:
1. 在元素集合 array[i]--array[n-1] 中选择关键码最⼤(小)的数据元素
2. 若它不是这组元素中的最后⼀个(第⼀个)元素,则将它与这组元素中的最后⼀个(第⼀个)元素交换
3. 在剩余的 array[i]--array[n-2](array[i+1]--array[n-1]) 集合中,重复上述步骤,直到集合剩余 1 个元素
代码实现:
//1)直接选择排序
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (end >= begin)
{
//找max和min
int mini = begin;
int maxi = begin;
for (int i = begin + 1;i <= end;i++)
{
if (arr[i] < arr[mini])
{
mini = i;
}
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
//交换mini和begin,maxi和end
Swap(&arr[begin], &arr[mini]);
Swap(&arr[end], &arr[maxi]);
begin++;
end--;
}
}交换代码:
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}直接选择排序的特性总结:
1. 直接选择排序思考⾮常好理解,但是效率不是很好。实际中很少使⽤
2. 时间复杂度: O(N^2 )
3. 空间复杂度: O(1)
2)堆排序:
堆排序(Heapsort)是指利⽤堆积树(堆)这种数据结构所设计的⼀种排序算法,它是选择排序的⼀种。它是通过堆来进⾏选择数据。需要注意的是排升序要建⼤堆,排降序建小堆。
这一部分在“二叉树——堆”这一篇有详细讲解,大家可以回看一下。
代码实现:
//2)堆排序
void HeapSort(int* arr, int n)
{
//先向下调整算法建堆(从小到大,建大堆)
for (int i = (n - 1 - 1) / 2;i >= 0;i--)
{
AdjustDown(arr, i, n);
}
//再堆顶交换,出堆,
int end = n - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, 0, end);
end--;
}
}
//向下调整算法
AdjustDown(int* arr, int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
//升序,建大堆
if (arr[child] < arr[child + 1] && child + 1 < n)
{
child = child + 1;
}
if (arr[parent] < arr[child])
{
Swap(&arr[parent], &arr[child]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}堆排序的特性总结
• 时间复杂度: O (nlogn )• 空间复杂度: O (1)
3.交换排序
1)冒泡排序:
冒泡排序可以说是最基础的排序之一了,其原理就是将相邻的数据从左到右依次进行比较,这样就会排好最后一个数据,循环n次完成排序。
代码实现:
//1)冒泡排序
void BubbleSort(int* arr, int n)
{
for (int i = 0;i < n;i++)
{
for (int j = 0;j < n - i - 1;j++)
{
if (arr[j] > arr[j+1])
{
Swap(&arr[j], &arr[j+1]);
}
}
}
}• 时间复杂度: O ( N^ 2 )• 空间复杂度: O (1)
2)快速排序:
快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两⼦序列,左⼦序列中所有元素均小于基准值,右⼦序列中所有元素均⼤于基准值,然后最左右⼦序列重复该过程,直到所有元素都排列在相应位置上为止。
代码实现基本框架:
//2)快速排序
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
//找基准值
int key = _QuickSort(arr, left, right);
//左序列[left,key-1],右序列[key+1,right]
QuickSort(arr, left, key - 1);
QuickSort(arr, key + 1, right);
}将区间中的元素进行划分的_QuickSort函数求基准值的方法主要有以下几种实现方式:
1.hoare版本:
基本思路:
创建左右指针 left 和 right,确定基准值;
从右向左找出比基准值小的数据,从左向右找出比基准值⼤的数据,左右指针数据交换,进入下次循环。
代码实现:
//找基准值 1.hoare版本
int _QuickSort1(int* arr, int left, int right)
{
int key = left;
left++;
while (left <= right)
{
//left从左往右找比基准值大的
while (left <= right && arr[left] < arr[key])
{
left++;
}
//right从右往左找比基准值小的
while (left <= right && arr[right] > arr[key])
{
right--;
}
//都找到了就交换
if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
}
}
Swap(&arr[right], &arr[key]);
return right;
}2.挖坑法:
基本思路:
创建左右指针。⾸先从右向左找出比基准小的数据,找到后⽴即放⼊左边坑中,当前位置变为新的"坑",然后从左向右找出比基准大的数据,找到后⽴即放入右边坑中,当前位置变为新的"坑",结束循环后将最开始存储的分界值放入当前的"坑"中,返回当前"坑"下标(即分界值下标)
代码实现:
//找基准值 2.挖坑法
int _QuickSort2(int* arr, int left, int right)
{
int hole = left;
int key = arr[hole];
while (left < right)
{
while (left < right && arr[right] > key)
{
right--;
}
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] < key)
{
left++;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
return hole;
}3.lomuto前后指针法:
创建前后指针,先出发的指针从左往右找比基准值小的与后出发的指针进行交换,使得小的都排在基准值的左边。
代码实现:
//找基准值 3.lomuto前后指针法
int _QuickSort3(int* arr, int left, int right)
{
int prev = left;
int cur = prev+1;
int key = left;
while (cur <= right)
{
//cur与基准值比较
if (arr[cur] < arr[key] && ++prev!=cur)
{
Swap(&arr[cur], &arr[prev]);
}
++cur;
}
Swap(&arr[key], &arr[prev]);
return prev;
}快速排序特性总结:
1. 时间复杂度: O(nlogn)
2. 空间复杂度: O(logn)
3)非递归版本的快速排序:
实现非递归版本的快速排序需要借助数据结构——栈来实现。栈的定义及其相关函数见文章结尾。
代码实现:
//2)快速排序----非递归版本快速排序----栈
void QuickSortNorR(int* arr, int left, int right)
{
stack st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
//取栈顶两次
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
//找基准值
int key = begin;
int prev = begin;
int cur = prev + 1;
while (cur <= right)
{
while (arr[cur] < arr[key] && ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[key], &arr[prev]);
key = prev;
if (key + 1 < right)
{
STPush(&st, right);
STPush(&st, key + 1);
}
if (begin < key - 1)
{
STPush(&st, key - 1);
STPush(&st, left);
}
}
STDestroy(&st);
}4.归并排序
归并排序的算法思想:
归并排序(MERGE-SORT)是建⽴在归并操作上的⼀种有效的排序算法,该算法是采⽤分治法(Divide and Conquer)的⼀个⾮常典型的应⽤。将已有序的⼦序列合并,得到完全有序的序列;即先使每个⼦序列有序,再使⼦序列段间有序。若将两个有序表合并成⼀个有序表,称为⼆路归并。
归并排序的核心步骤:
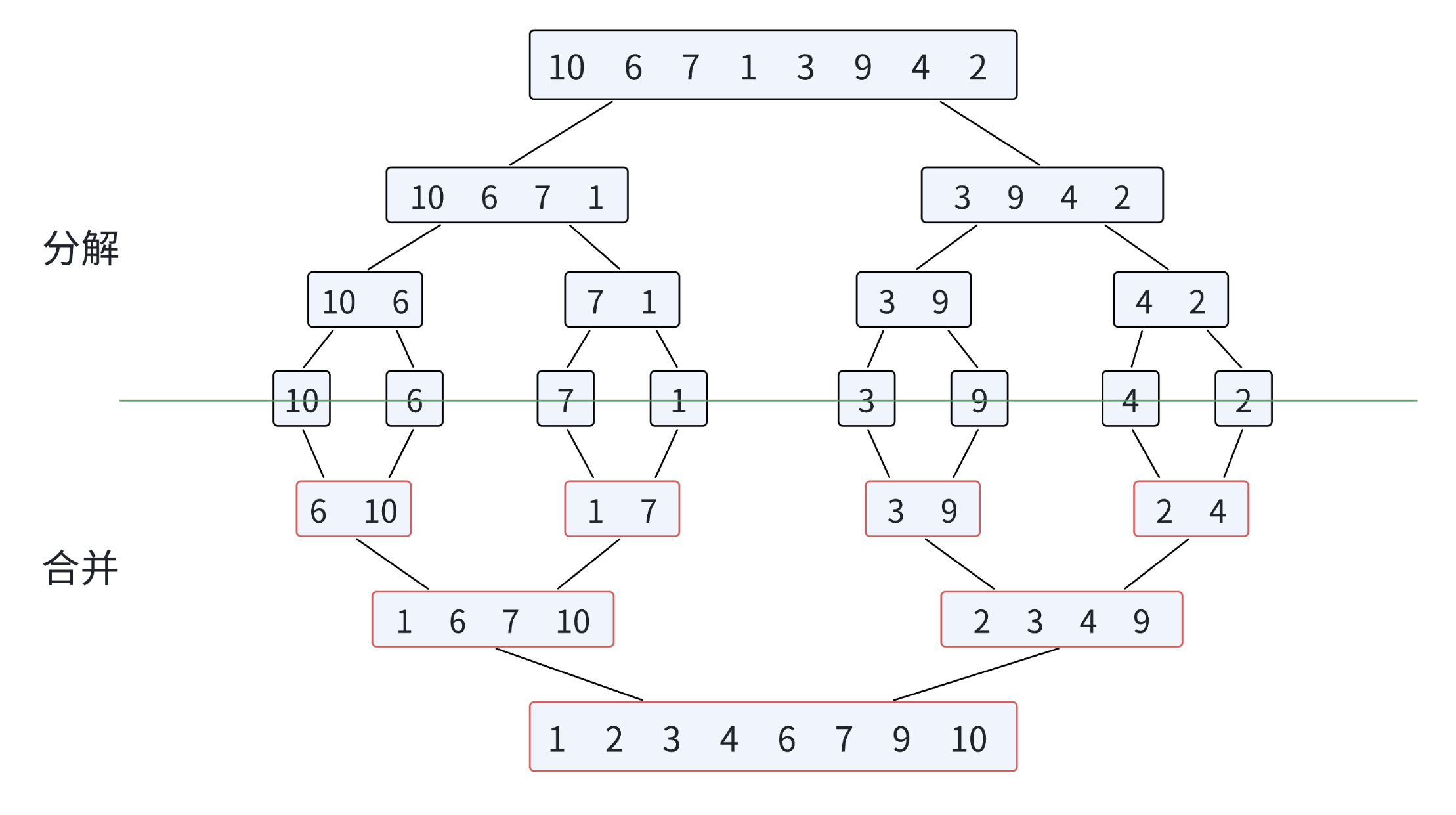
代码实现:
//归并排序
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
_MergeSort(arr, 0, n-1, tmp);
free(tmp);
}void _MergeSort(int* arr, int left, int right, int* tmp)
{
//分解
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//根据mid将序列划分为左右两个序列[left,mid][mid+1,right]
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid+1, right, tmp);
//合并两个序列[left,mid][mid+1,right]
int begin1 = left, begin2 = mid + 1;
int end1 = mid, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else {
tmp[index++] = arr[begin2++];
}
}
//要么begin1数据没放完
//要么begin2数据没放完
if (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
if (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//将tmp回放到arr中
for (int i = left;i <= right;i++)
{
arr[i] = tmp[i];
}
}归并排序特性总结:
1. 时间复杂度: O(nlogn)
2. 空间复杂度: O(n)
以上都是比较排序,下面说一个非比较排序。
5.非比较排序——计数排序
计数排序⼜称为鸽巢原理,是对哈希直接定址法的变形应⽤。
操作步骤:
1)统计相同元素出现次数
2)根据统计的结果将序列回收到原来的序列中
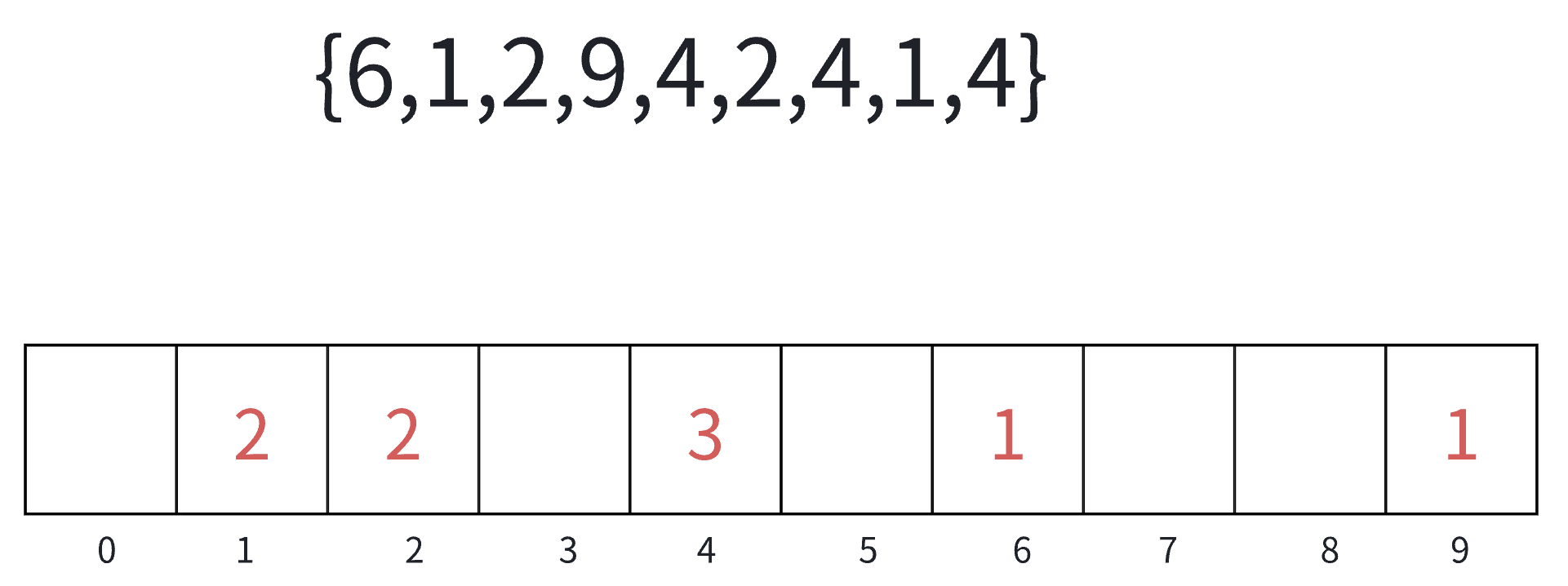
代码实现:
//非比较排序---技术排序
void CountSort(int* arr, int n)
{
int min = arr[0];
int max = arr[0];
for (int i = 1;i < n; i++)
{
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
//确定count数组大小
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
//也可以用malloc,然后用memset初始化count(memset(count,0,n*sizeof(int)))
if (count == NULL)
{
perror("calloc");
exit(1);
}
//存数据出现的次数到count数组中
for (int i = 0;i < n;i++)
{
count[arr[i] - min]++;
}
//将count回放到arr中
int index = 0;
for (int i = 0;i < range;i++)
{
while (count[i]--)
{
arr[index++] = i + min;
}
}
}计数排序的特性:
计数排序在数据范围集中时,效率很高,但是适⽤范围及场景有限。
时间复杂度: O(N + range)
空间复杂度: O(range)
稳定性:稳定
三、测试代码:排序性能对比
// 测试排序的性能对⽐
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
int* a8 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
a8[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
BubbleSort(a7, N);
int end7 = clock();
int begin8 = clock();
CountSort(a8, N);
int end8 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BubbleSort:%d\n", end7 - begin7);
printf("CountSort:%d\n", end8 - begin8);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
free(a8);
}经过测试,结果如下:
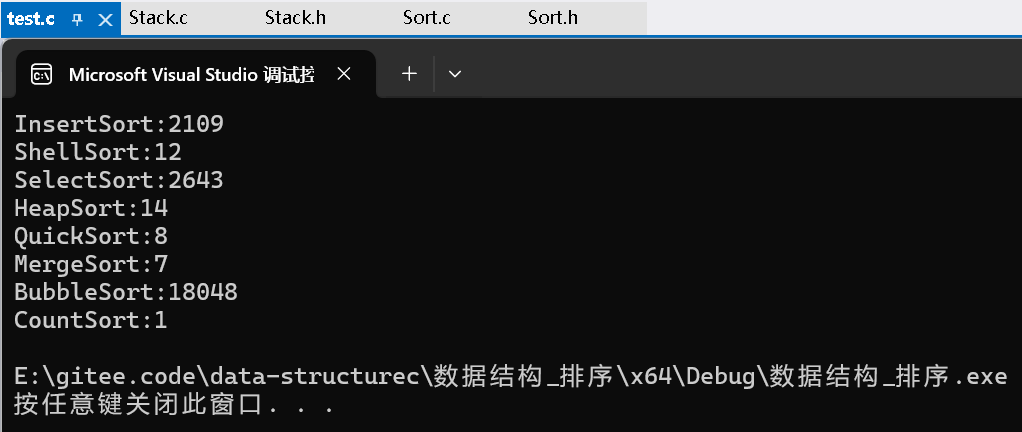
四、排序算法复杂度及稳定性分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,⽽在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
| 排序方法 | 平均情况 | 最好情况 | 最差情况 | 辅助空间 | 稳定性 |
| 冒泡排序 |
O
(
n^
2 )
|
O
(
n
)
| O(n^2 ) |
O
(1)
|
稳定
|
|
直接选择排序
| O(n^2 ) | O(n^2 ) | O(n^2 ) | O(1) | 不稳定 |
|
直接插入排序
| O(n^2 ) | O(n ) | O(n^2 ) | O(1) | 稳定 |
|
希尔排序
| O(nlogn)~O(n^2 ) | O(n^1.3 ) | O(n^2 ) | O(1) | 不稳定 |
|
堆排序
| O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
|
归并排序
| O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
|
快速排序
| O(nlogn) | O(nlogn) | O(n^2 ) | O(logn)~O(n) | 不稳定 |
| 计数排序 | O(n + range) | O(n + range) | O(n + range) | O(range) | 稳定 |
五、完整代码
Sort.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
//插入排序
//1)直接插入排序
void InsertSort(int* arr, int n);
//2)希尔排序
void ShellSort(int* arr, int n);
//选择排序
//1)直接选择排序
void SelectSort(int* arr, int n);
//2)堆排序
void HeapSort(int* arr, int n);
//交换排序
//1)冒泡排序
void BubbleSort(int* arr, int n);
//2)快速排序
void QuickSort(int* arr, int left, int right);
//2)快速排序----非递归版本快速排序----栈
void QuickSortNorR(int* arr, int left, int right);
//归并排序
void MergeSort(int* arr, int n);
//非比较排序---技术排序
void CountSort(int* arr, int n);Sort.c
#include"Sort.h"
#include"Stack.h"
//1)直接插入排序
void InsertSort(int* arr, int n)
{
for (int i = 0;i < n - 1;i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else {
break;
}
}
arr[end + 1] = tmp;
}
}
//2)希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0;i < n - gap;i++)//将数据分成gap组,每组进行预排序(i++是依次对每组的数据进行排序)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else {
break;
}
}
arr[end + gap] = tmp;
}
}
}
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//1)直接选择排序
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (end >= begin)
{
//找max和min
int mini = begin;
int maxi = begin;
for (int i = begin + 1;i <= end;i++)
{
if (arr[i] < arr[mini])
{
mini = i;
}
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
//交换mini和begin,maxi和end
Swap(&arr[begin], &arr[mini]);
Swap(&arr[end], &arr[maxi]);
begin++;
end--;
}
}
//向下调整算法
AdjustDown(int* arr, int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
//升序,建大堆
if (arr[child] < arr[child + 1] && child + 1 < n)
{
child = child + 1;
}
if (arr[parent] < arr[child])
{
Swap(&arr[parent], &arr[child]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
//2)堆排序
void HeapSort(int* arr, int n)
{
//先向下调整算法建堆(从小到大,建大堆)
for (int i = (n - 1 - 1) / 2;i >= 0;i--)
{
AdjustDown(arr, i, n);
}
//再堆顶交换,出堆,
int end = n - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, 0, end);
end--;
}
}
//1)冒泡排序
void BubbleSort(int* arr, int n)
{
for (int i = 0;i < n;i++)
{
for (int j = 0;j < n - i - 1;j++)
{
if (arr[j] > arr[j+1])
{
Swap(&arr[j], &arr[j+1]);
}
}
}
}
//找基准值 1.hoare版本
int _QuickSort1(int* arr, int left, int right)
{
int key = left;
left++;
while (left <= right)
{
//left从左往右找比基准值大的
while (left <= right && arr[left] < arr[key])
{
left++;
}
//right从右往左找比基准值小的
while (left <= right && arr[right] > arr[key])
{
right--;
}
//都找到了就交换
if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
}
}
Swap(&arr[right], &arr[key]);
return right;
}
//找基准值 2.挖坑法
int _QuickSort2(int* arr, int left, int right)
{
int hole = left;
int key = arr[hole];
while (left < right)
{
while (left < right && arr[right] > key)
{
right--;
}
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] < key)
{
left++;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
return hole;
}
//找基准值 3.lomuto前后指针法
int _QuickSort3(int* arr, int left, int right)
{
int prev = left;
int cur = prev+1;
int key = left;
while (cur <= right)
{
//cur与基准值比较
if (arr[cur] < arr[key] && ++prev!=cur)
{
Swap(&arr[cur], &arr[prev]);
}
++cur;
}
Swap(&arr[key], &arr[prev]);
return prev;
}
//2)快速排序
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
//找基准值
//int key = _QuickSort1(arr, left, right);
int key = _QuickSort3(arr, left, right);
//左序列[left,key-1],右序列[key+1,right]
QuickSort(arr, left, key - 1);
QuickSort(arr, key + 1, right);
}
//2)快速排序----非递归版本快速排序----栈
void QuickSortNorR(int* arr, int left, int right)
{
stack st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
//取栈顶两次
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
//找基准值
int key = begin;
int prev = begin;
int cur = prev + 1;
while (cur <= right)
{
while (arr[cur] < arr[key] && ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[key], &arr[prev]);
key = prev;
if (key + 1 < right)
{
STPush(&st, right);
STPush(&st, key + 1);
}
if (begin < key - 1)
{
STPush(&st, key - 1);
STPush(&st, left);
}
}
STDestroy(&st);
}
void _MergeSort(int* arr, int left, int right, int* tmp)
{
//分解
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//根据mid将序列划分为左右两个序列[left,mid][mid+1,right]
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid+1, right, tmp);
//合并两个序列[left,mid][mid+1,right]
int begin1 = left, begin2 = mid + 1;
int end1 = mid, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else {
tmp[index++] = arr[begin2++];
}
}
//要么begin1数据没放完
//要么begin2数据没放完
if (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
if (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//将tmp回放到arr中
for (int i = left;i <= right;i++)
{
arr[i] = tmp[i];
}
}
//归并排序
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
_MergeSort(arr, 0, n-1, tmp);
free(tmp);
}
//非比较排序---技术排序
void CountSort(int* arr, int n)
{
int min = arr[0];
int max = arr[0];
for (int i = 1;i < n; i++)
{
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
//确定count数组大小
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
//也可以用malloc,然后用memset初始化count(memset(count,0,n*sizeof(int)))
if (count == NULL)
{
perror("calloc");
exit(1);
}
//存数据出现的次数到count数组中
for (int i = 0;i < n;i++)
{
count[arr[i] - min]++;
}
//将count回放到arr中
int index = 0;
for (int i = 0;i < range;i++)
{
while (count[i]--)
{
arr[index++] = i + min;
}
}
}Stack.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//定义栈的结构
typedef int STDataType;
typedef struct stack {
STDataType* arr;
int top;
int capacity;
}stack;
//初始化栈
void STInit(stack* ps);
//销毁栈
void STDestroy(stack* ps);
//入栈
void STPush(stack* ps, STDataType x);
//栈是否为空
bool STEmpty(stack* ps);
//出栈
void STPop(stack* ps);
//取栈顶数据
STDataType STTop(stack* ps);
//获取栈中有效元素个数
int STSize(stack* ps);Stack.c
#include"Stack.h"
//初始化
void STInit(stack* ps)
{
ps->arr = NULL;
ps->top = ps->capacity = 0;
}
//销毁栈
void STDestroy(stack* ps)
{
if (ps->arr != NULL)
{
free(ps->arr);
}
ps->arr = NULL;
ps->top = ps->capacity = 0;
}
//入栈
void STPush(stack* ps, STDataType x)
{
assert(ps);
//判断空间是否足够
if (ps->capacity == ps->top)
{
int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
STDataType* temp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
if (temp == NULL)
{
perror("realloc");
exit(1);
}
ps->arr = temp;
ps->capacity = newCapacity;
}
//空间足够
ps->arr[ps->top++] = x;
}
//判断栈是否为空
bool STEmpty(stack* ps)
{
assert(ps);
return ps->top == 0;
}
//出栈
void STPop(stack* ps)
{
assert(!STEmpty(ps));
ps->top--;
}
//取栈顶数据
STDataType STTop(stack* ps)
{
assert(!STEmpty(ps));
return ps->arr[ps->top - 1];
}
//获取栈中有效元素个数
int STSize(stack* ps)
{
assert(ps);
return ps->top;
}test.c
#include"Sort.h"
void printArr(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
void test1()
{
//int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
//int a[] = { 5, 3, 9, 6, 2, 4 };
//int a[] = { 6,1,2,7,9,3 };
int a[] = { 100,101,109,105,101,105 };
printf("排序之前:");
int n = sizeof(a) / sizeof(a[0]);
printArr(a, n);
//InsertSort(a, n);
//ShellSort(a, n);
//SelectSort(a, n);
//HeapSort(a, n);
//BubbleSort(a, n);
//QuickSort(a, 0, n - 1);
QuickSortNorR(a, 0, n - 1);
//MergeSort(a, n);
//CountSort(a, n);
printf("排序之后:");
printArr(a, n);
}
// 测试排序的性能对⽐
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
int* a8 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
a8[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
BubbleSort(a7, N);
int end7 = clock();
int begin8 = clock();
CountSort(a8, N);
int end8 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BubbleSort:%d\n", end7 - begin7);
printf("CountSort:%d\n", end8 - begin8);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
free(a8);
}
int main()
{
//test1();
TestOP();
return 0;
}六、博主手记









结语:
以上就是排序算法的全部内容了,大家有什么疑问可以在评论区讨论,感谢观看,希望友友们能一件四连支持一下博主~























 1065
1065










