目录
前言:
本篇的内容是实现链式结构的二叉树,主要内容有前中后序遍历、求二叉树节点个数、求叶子节点个数、求第k层的节点个数、二叉树的深度/高度、二叉树中查找值为x的节点以及二叉树的销毁,还有最后的进阶函数:层序遍历、判断是否为完全二叉树。
1、定义二叉树的链式结构
用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址, 其结构如下:
//定义二叉树的链式结构
typedef char BTDataType;
typedef struct BinaryTreeNode {
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;2、前中后序遍历
①前序遍历
访问根节点的操作发生在遍历其左右子树之前。访问顺序为:根节点、左子树、右子树
//前序遍历——根左右
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}②中序遍历
访问根节点的操作发生在遍历其左右子树之间。访问顺序为:左子树、根节点、右子树
//中序遍历——左右根
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}③后序遍历
访问根节点的操作发生在遍历其左右子树之后。访问顺序为:左子树、右子树、根节点
//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}图解(以前序遍历为例)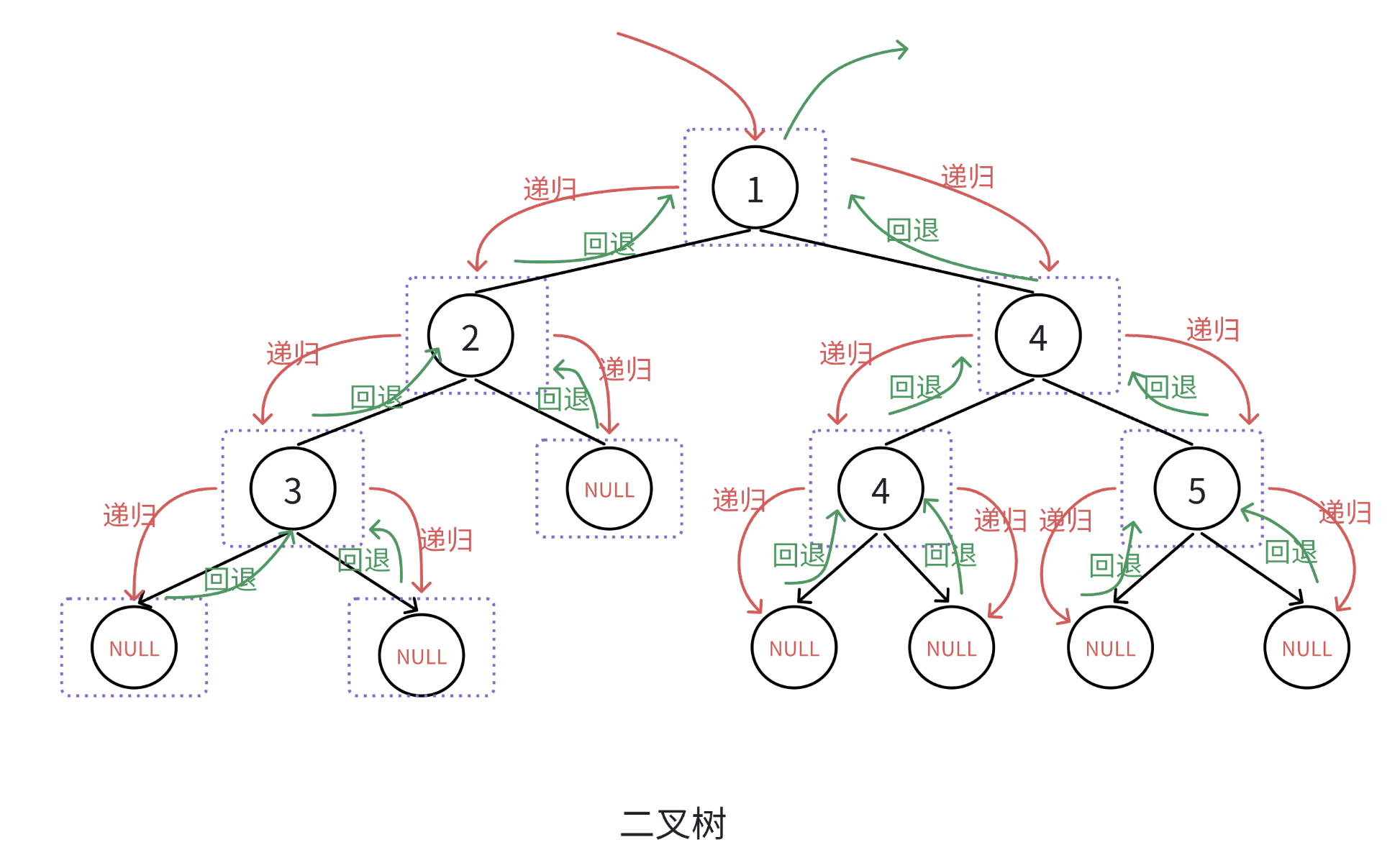
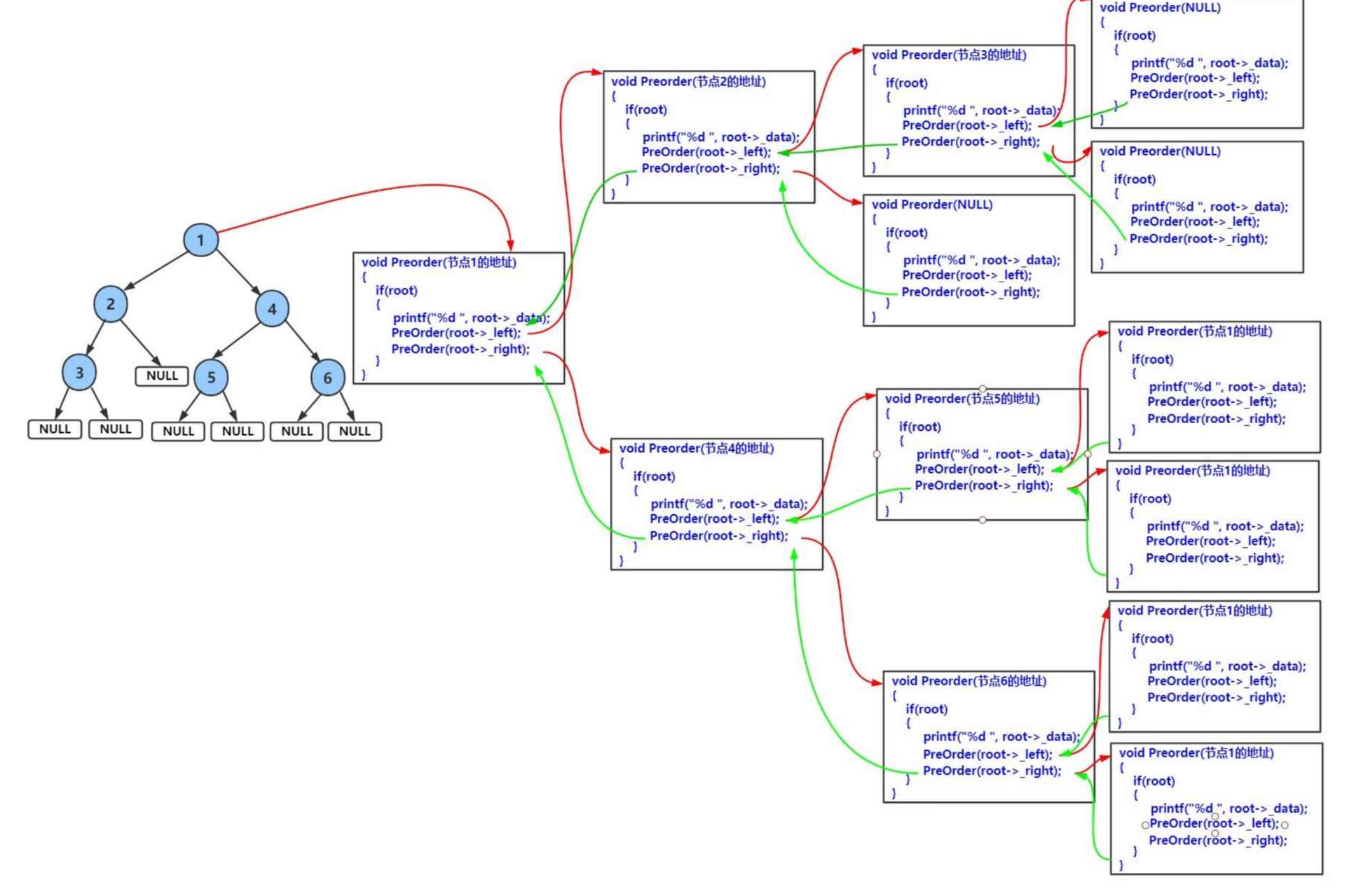
3、二叉树的节点个数
求二叉树的节点个数有好几个方法,我给大家两个比较好的方法:
版本一:改造函数定义,引入新变量size,但需要在使用函数之前定义该变量后再传参。缺点:不能重复计算同一个参数,重复使用需要重新定义为0。
版本二:节点个数 = 1 + 左子树节点个数 + 右子树节点个数
(可重复计算,没有限制)
版本一:
//若多次传入同一个size会出现累加的情况
void BinaryTreeSize(BTNode* root, int* psize)
{
if (root == NULL)
{
return 0;
}
(*psize)++;
BinaryTreeSize(root->left,psize);
BinaryTreeSize(root->right, psize);
}版本二:(完美的版本)
// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}4、二叉树的叶子节点的个数
叶子节点就是度为0的节点。
叶子节点个数 = 左子树的叶子节点个数 + 右子树的叶子节点个数
使用函数递归,函数内部判断是否为叶子节点。
// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
//判断是否为叶子节点
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}5、二叉树第K层的节点个数
第K层节点个数 = 左子树第K层节点个数 + 右子树第K层节点个数
直接在函数递归部分使用 k-1 来找到第k层(k=1了就到第k层了),然后求其节点个数。
// ⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}6、二叉树的高度/深度
二叉树的高度 = 1 + max(左子树的高度,右子树的高度)
// ⼆叉树的深度/⾼度
int BinaryTreeDepth(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftDep = BinaryTreeDepth(root->left);
int rightDep = BinaryTreeDepth(root->right);
return 1 + (leftDep > rightDep ? leftDep : rightDep);
}7、查找二叉树中值为x的节点
左右子树分别遍历寻找值为x的节点,找到了直接返回,都没找到返回NULL。
// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
//哪个子树找到了就返回找到的节点,否则NULL
BTNode* leftFind = BinaryTreeFind(root->left, x);
if (leftFind != NULL)
{
return leftFind;
}
BTNode* rightFind = BinaryTreeFind(root->right, x);
if (rightFind != NULL)
{
return rightFind;
}
return NULL;
}8、二叉树的销毁
如果根节点不为空,递归其左右子树,不为空就free
// ⼆叉树销毁
void BinaryTreeDestory(BTNode** root)
{
if (*root == NULL)
{
return;
}
BinaryTreeDestory(&(*root)->left);
BinaryTreeDestory(&(*root)->right);
free(*root);
*root = NULL;
}9、层序遍历(二叉树与队列相结合)
除了先序遍历、中序遍历、后序遍历外,还可以对⼆叉树进⾏层序遍历。设⼆叉树的根结点所在层数为1,层序遍历就是从所在⼆叉树的根结点出发,⾸先访问第⼀层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
层序遍历就是指一层一层的、从左向右的遍历。
实现层序遍历需要借助数据结构——队列
实现方法:先将二叉树的头节点入队列,保证队列不为空,然后循环判断队列是否为空,不为空进入循环:取队头,打印队头,出队头,队头的左右节点不为空就入队列。
// 层序遍历
void LevelOrder(BTNode* root)
{
//层序遍历要用到队列
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
//取队头,打印队头
BTNode* top = QueueFront(&q);
QueuePop(&q);
printf("%c ", top->data);
//让节点不为空的孩子节点入队列
if(top->left) //这里应该是操作 top,而不是一直是root
{
QueuePush(&q, top->left);//这里应该是操作 top,而不是一直是root
}
if (top->right)//这里应该是操作 top,而不是一直是root
{
QueuePush(&q, top->right);//这里应该是操作 top,而不是一直是root
}
}
QueueDestroy(&q);
}10、判断是否为完全二叉树(二叉树与队列相结合)
实现方法:先让根节点入队列,保证队列不为空,然后循环判断队列是否为空,不为空进入循环:取队头,(不为空就继续,为空就break跳出循环)出队头,让队头的左右孩子节点入队列。取到空的队头跳出循环,循环判断队列不为空进入循环:队头是否为空,不为空就直接返回fasle,否则出循环后返回true。
// 判断⼆叉树是否是完全⼆叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* top = QueueFront(&q);
QueuePop(&q);
if (top == NULL)
{
break;
}
QueuePush(&q, top->left);
QueuePush(&q, top->right);
}
//队列不为空,继续取队列中的队头
while (!QueueEmpty(&q))
{
if (QueueFront(&q) != NULL)
{
QueueDestroy(&q);
return false;
}
QueuePop(&q);
}
QueueDestroy(&q);
return true;
}最后、博主手记




结语:
这篇文章的分享到这里就结束了,大家如果有更好的想法或者方法可以在评论区分享出来,欢迎大家互动!感谢关注!























 1589
1589










