模糊逻辑(Fuzzy Logic)

参考：
https://blog.youkuaiyun.com/yuyanjingtao/article/details/90177004
https://blog.youkuaiyun.com/ice_pill/article/details/72716909

介绍
在我们现实生活中，往往会遇到一些比较让人纠结的问题，比如一个人的IQ90算聪明，60算笨拙，那么一个IQ=89的人算什么呢？如果根据离散逻辑来考虑，那么即使是89，只要没达到90就是笨拙，这在我们人类的理解范围内会感觉很奇怪（正常感性认知），所以在1965年美国数学家L. Zadeh首先提出了Fuzzy集合的概念，目的就是未了解决这种模棱两可的问题。

流程：

关键概念：
模糊化： 如何确定输入数值与隶属度的关系呢，这就要用到隶属度函数，隶属度函数的图形可以是任意的，但常用的方法是三角形或者梯形（作用：用隶属度函数使一个变量转化为各个集合的隶属度）
模糊语言变量：
为什么我能确定IQ70-90可能是平凡的范围，80-100可能是聪明的范围呢？其实这个是根据开发者经验设计的，这也就是模糊逻辑最麻烦的地方。很多概念我们自己都模棱两可，不能给出一个绝对的值，比如有的人认为可能超过IQ70都可以叫聪明了，不同的人对与不同的模糊语言变量有不同的理解。当然，我们在设计一些比较真是的情况下可以去请教相关的专家或者领域权威人物，比如我们在做模拟篮球的语言变量设定的时候，是我们坐在这里自己yy得出的数据准确，还是去请教姚明对呀这方面的感觉准确呢？当然是后者。
模糊集合：

IQ80-100分内才可能被算作聪明,其中90分被作为聪明的可能性最大，超过100分可能就是天才 范围了（我只是举个例子），所以这里用了个三角形的模糊函数来计算聪明对应不同分数的隶属度。然而实际情况可能是这样多个模糊函数交织在一起，所以我们需要对重叠在一起的部分选择一个合适的算法，来具体计算出89这个值在聪明和平凡两个集合的或集合，与集合中所占有的隶属度。
隶属度（函数）：
在模糊逻辑的眼中，大雨，小雨，和中雨之间是没有严格的界限的，也就是说某一种雨量的大小并不完全归属于某一个类，而是以隶属度来衡量的。比如对于10mm降雨，隶属于小雨的隶属度为0.5, 中雨的隶属度为0.4，大雨的隶属度为0.1；对于100mm降雨，小雨的隶属度为0, 中雨的隶属度为0.3，大雨的隶属度为0.7。
模糊规则：
模糊规则主要是有一组因果推理的逻辑关系表达式，比如如果前提 那么就结果
用猿语表示就是if（条件）{执行结果}
比如：如果iq高 与 eq高 那么聪明
模糊逻辑的“与，或，非”运算：
模糊逻辑的运算实际上就是模糊逻辑中分解出的各个隶属度的运算。我们将逻辑的两个输入定义为A，B，输出为C(A与B -> C)，举个例子，A = Poor: 0.5（Poor的隶属为0.5 ）B = Good：0.2， 那么C= A与B是多少呢？
其实有好多计算C的方法，这里介绍一个最简单的“最小隶属法(MIN implication)”，于是 C=A与B中最小那个（0.2）。于是C= Good: 0.2.
那D = A或B怎么计算呢？还是介绍一个最简单的“最大隶属法(MAX implication)”，即 C=A或B中最大的那个(0.5)。 于是D= Poor: 0.5
"非"的运算就更简单了，直接如下图所示取相反的折线就完了。


模糊推理：
下面我们以一个具体的例子来讲解：
比如一个人的聪明度是有他的IQ和EQ觉定的，那么对一个IQ=89，EQ=89（假设，IQ89对于高的隶属度是0.8，对于低的隶属度是0，EQ89对呀高的隶属度是0.7，对于低的隶属的是0.3）的人是否聪明，我们有如下规则
规则1. 如果iq高 与 eq高 那么聪明
规则2. 如果iq高 与 eq低 那么笨拙
规则3. 如果iq低 与 eq低 那么笨拙
规则4. 如果iq低 与 eq高 那么笨拙
其实就是对枚举每种可能性，或者交对两个不同的模糊变量做笛卡尔积，然后根据其隶属度计算出结果 可能性，如规则1，iq高的隶属度是0.8，eq高的可能性是0.7，由于是与运算，所以我们选用min函数作为模糊函数，所以在这里聪明的可能性是min（0.8，0.7）=0.7，对于规则2，iq高的隶属度是0.8，eq低的隶属度是0.3，所以笨拙的可能性是min（0.8，0.3）=0.3以此类推，最后我们得到这样一张表

可以看出，即使对于EQ/IQ都是89的人，他聪明的可能性 0.7，笨拙的可能性是0(min(0,0.3,0))。
去模糊化：
把一个复合的模糊集合通过一些去模糊函数计算得到一个离散的量，也就是我们想要的聪明/笨拙程度的描述值。去模糊其实就是我们之前模糊的逆过程。
这里介绍几种比较常见的方法：
1：加权平均判决法

FS就是模糊推理得到的，OW (Output Wight)是权重。权重通常是取每个集合的中间值。
2：最大值均值法（MOM）
由于实际使用较少，所以这里不多做说明
3：中心法
中心法是一种最为准确，但却也是最为复杂的 一种方法，其原理就是对不同的期望值进行采样平均处理，计算每个样点对于总体的隶属度的贡献之和，比如我对（10，20.30.40……100）每10期望进行一次采样，计算采样点的期望和，再除以样本的隶属度之和。
在中心法中，取的样本密度越大，其准确性越大。

4：最大值平均法（MAXAV）
这是一种综合2 和 3两种方法得到的一种折中算法，其结果准确的近似与中心法，且其运算复杂性要远低于中心法。一个模糊集合的最大值或代表值应该是一个这样的值，比如三角形模糊函数的正中点，或者梯形函数的上边，对于三角形函数，其最大期望平均值就是其正中点，对于梯形函数其最大期望平均值为上边的中点。这样计算即避免了中心法大量采样的性能消耗问题，也在一定程度上贴近了中心法的计算结果。

最终，不管我们选那种方法，做到这里们都得到了我们用来描述聪明-笨拙程度的数值或者从智能决策的角度考虑就是某种事情发生-不发生的可能性。

举例：
step1 2 :模糊化+模糊推理：
如下图，表格为规则，例如：Taste(M)与Hunger(M)输出M，Hunger(M)与Taste(L)输出L；隶属度函数在表格下面。以Taste 和 Hunger分别取值为5.625和4.375为例，会有如下图结果：


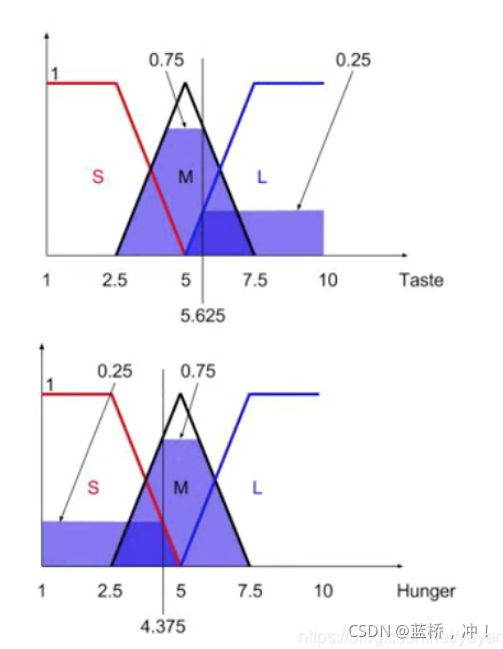
表中：
红色S是Taste(M)与Hunger(S)的输出结果可以用最小法则Min(0.75, 0.25)=0.25
绿色M是Taste(M)与Hunger(M)的输出结果可以用最小法则Min(0.75, 0.75)=0.75
黄色M是Taste(L)与Hunger(S)的输出结果可以用最小法则Min(0.25, 0.25)=0.25
紫色L是Taste(L)与Hunger(M)的输出结果可以用最小法则Min(0.25, 0.75)=0.25
其他输出为0。
这些输出我们在模糊逻辑中定义为Fire Strength(FS)。
step3:去模糊化：使用加权平均判决法

其中FS就是上一步输出的Fire Strength, OW (Output Wight)是权重。权重通常是取每个集合的中间值，分配食物的例子OW(S)=2.5, OW(M)=5, OW(L)=7.5。
如果Taste = 5.625, Hunger = 4.375
FS1(S)=0.25, FS2(M)=0.75, FS3(M)=0.25, FS4(L)=0.25.
用上面的公式可以求得
Output = (0.25* 2.5+0.75* 5+0.25* 5+0.25 *7.5)/(0.25+0.75+0.25+0.25)=5
这个输出有什么用呢？你可以通过这个输出决定是否分配食物，设定一个阈值，比如为4，如果小于等于这个阈值就不分配食物，大于这个阈值就分配食物。这里输出是5，那么就可以给自己分配食物了。还可以通过设置多个阈值，来决定分配给自己食物的多少。