代码
#include <iostream>
using namespace std;
const double PI = 3.1415926535898;
//这种连续数值的二分搜索问题,一定要定义一个接近于0的小数字L,作为终止循环的边界。
//且有些题专门卡精度,此边界要定义的比题目要求输出的小数位更多一些。
const double L = 1e-6;
double binarySearch(double a[], int len, double max, int people) {
double left = 0;
double right = max;
while(right-left>L) {
double mid = (left+right)/2.0;
int count = 0;
//切蛋糕,类似于蓝桥杯的分巧克力。一块蛋糕可以切成很多块,但每个人分得的蛋糕必须来自于同一块。
//蓝桥杯的题目是方形的,此题是圆形。因此要用每块蛋糕的总面积,除以当前的mid,也就是此块蛋糕最多被分成几块。
for(int i=0; i<len; i++){
count = count + (int)((PI*a[i]*a[i])/mid);
}
if(count>=people){
left = mid;
}
else{
right = mid;
}
}
return left;
}
int main() {
int M;
scanf("%d", &M);
for(int i=0; i<M; i++){
int N, F;
scanf("%d %d", &N, &F);
double radii[N];
double sum = 0;
for(int j=0; j<N; j++){
scanf("%lf", &radii[j]);
sum += PI*radii[j]*radii[j];
}
//F个朋友,自己也要一块,因此共F+1块蛋糕
double max = sum/(double)(F+1);
int people = F+1;
double ans = binarySearch(radii, N, max, people);
printf("%.4lf\n", ans);
}
return 0;
}
注解
1、连续型的二分搜索问题。
2、卡精度,注意定义左右边界差值L。
3、类似于蓝桥杯2017省赛“分巧克力”。类似问题还有HDU中的一些解方程问题。
结果









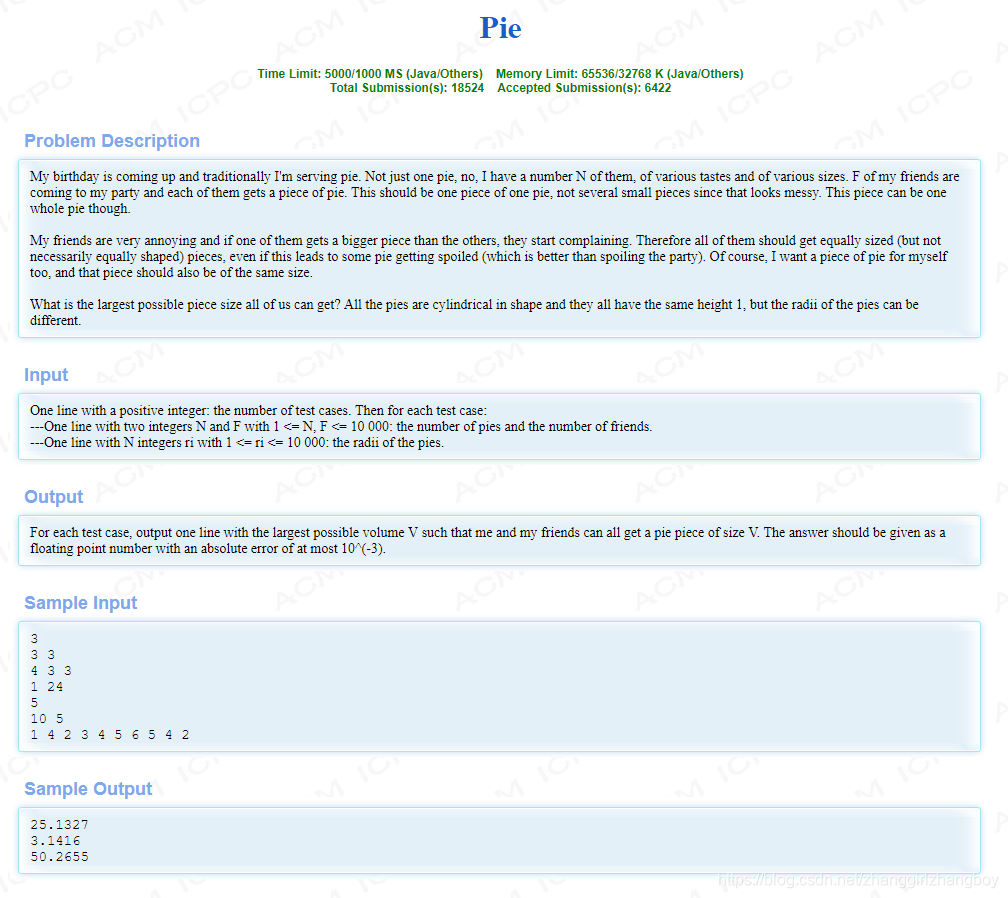
 本文介绍了一种使用二分搜索算法解决连续数值型问题的方法,具体案例为如何公平地将不同大小的圆形蛋糕分给一定数量的人。文章通过定义精度边界来确保算法的准确性,并提供了一个完整的C++实现示例。
本文介绍了一种使用二分搜索算法解决连续数值型问题的方法,具体案例为如何公平地将不同大小的圆形蛋糕分给一定数量的人。文章通过定义精度边界来确保算法的准确性,并提供了一个完整的C++实现示例。
















 183
183

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








