并查集篇(2W字长文)：一套“开箱即用”的并查集模板带你无脑秒杀一系列图论算法题-优快云博客

文章目录

前言

并查集（Disjoint Set Union，DSU）是一种用于处理不相交集合合并和查询问题的数据结构。它主要用于解决连通性问题，当我们需要 判断两个元素是否在同一个集合里 的时候，就可以使用并查集。

并查集在算法竞赛和实际开发中都有着广泛的应用，特别是在图论相关问题中表现出色。本文将从图论角度深入分析并查集的原理，并提供一个开箱即用的模板及其在各种题目中的实战应用。

前置知识：图论基本概念，如顶点、边；连通分量，无向图，森林

参考学习链接：图论基本概念 (OI Wiki)

本文做的事情：

简单从图论角度回顾并查集原理，并且基于并查集的find、join等方法，实现两种不同且通用的并查集模板，并且直接用于 5 道题目的实战秒杀、讲解

从图论角度理解并查集

基本概念

在图论中，并查集可以理解为维护一个动态连通图的数据结构：

顶点（Vertex）：集合中的每个元素
边（Edge）：元素之间的连接关系
连通分量（Connected Component）：图中相互连通的顶点集合
森林（Forest）：多个不相交的树组成的图结构

补充概念：连通分量

在图论中，如果从顶点A可以到达顶点B（无论直接或间接），则称A和B是连通的。一个连通分量是图中的一个“最大”连通子图，其中任何两个顶点都相互连通，且它不与外部任何顶点连通。

并查集与连通分量的关系：并查集中的每一个独立的集合，都完美对应了图论中的一个连通分量。join(u, v)操作就是将两个连通分量合并成一个，而getComponentCount()就是获取当前图中连通分量的总数。

图论视角下的并查集操作

初始状态：每个顶点都是一个独立的连通分量（自环）
```
1    2    3    4    5
↻   ↻    ↻    ↻   ↻
```
Union操作：连接两个连通分量，相当于在图中添加一条边
```
连接1和2后：
1 ← 2    3    4    5
    ↻   ↻    ↻    ↻
```

Find操作：寻找顶点所属连通分量的代表元素（根节点）

路径压缩前：1 ← 2 ← 3 ← 4
路径压缩后：1 ← 2
           ↑   ↑
           3   4

并查集的核心功能

将两个元素添加到一个集合中（Union操作）
判断两个元素在不在同一个集合（Find + 比较操作）
动态维护连通分量的数量

★开箱即用的并查集模板

基于并查集原理，我们可以封装一个通用并查集模板类，支持任意类型（泛型）的元素，以下是详细内容：

import java.util.HashMap;
import java.util.Map;

/**
 * 并查集模板类：基于HashMap实现的泛型并查集
 * 
 * 核心思想：
 * 1. 使用Map<T, T>存储父子关系，key为当前节点，value为父节点
 * 2. 初始时每个节点的父节点是自己（自环），表示独立的连通分量
 * 3. 通过路径压缩优化Find操作，使树保持扁平化
 * 4. 实时维护连通分量数量，支持O(1)查询
 * 
 * 要求：如无默认实现，则泛型T必须正确重写equals()和hashCode()方法
 * 
 * 时间复杂度：
 * - Find: O(α(n)) (近乎O(1)) （α为阿克曼函数的反函数）
 * - Union: O(α(n)) (近乎O(1))
 * - isConnected: O(α(n)) (近乎O(1))
 * **注意**：严格来说，只有同时使用“路径压缩”和“按秩/大小合并”优化，时间复杂度才能达到O(α(n))。
 * 本模板为了代码简洁和易用性，仅实现了路径压缩。
 */
public class DisjointSetUnion<T> {
    // 存储父子关系的映射表：<当前节点, 父节点>
    private final Map<T, T> father = new HashMap<>();
    
    // 连通分量的数量，初始为0
    private int componentCount = 0;

    /**
     * 构造函数：创建空的并查集
     */
    public DisjointSetUnion() {
    }

    /**
     * 向并查集中添加一个新的顶点
     * 
     * @param x 要添加的顶点
     * @return 如果顶点不存在则添加并返回true，否则返回false
     */
    public boolean add(T x) {
        if (!father.containsKey(x)) { // 实际刷题中，可以忽略这些健壮性判断，效率更高
            // 初始化时，每个节点的父节点是自己（形成自环）
            // 这表示该节点是一个独立的连通分量
            father.put(x, x);
            componentCount++; // 连通分量数量增加
            return true;
        }
        return false; // 顶点已存在
    }

    /**
     * 合并两个顶点所在的连通分量（Union操作）
     * 
     * 在两个连通分量之间添加一条边，使它们合并为一个连通分量
     * 
     * @param u 第一个顶点
     * @param v 第二个顶点
     */
    public void join(T u, T v) {
        // 确保两个顶点都已添加到并查集中
        // 这样设计使得调用者无需预先添加所有顶点
        add(u);
        add(v);

        // 找到两个顶点所在连通分量的根节点
        u = find(u);
        v = find(v);
        
        // 如果两个顶点不在同一个连通分量中
        if (!u.equals(v)) {
            // 将v的根节点指向u的根节点，实现合并
            // 这里选择u作为新的根节点（也可以选择v）
            father.put(v, u);
            
            // 合并后连通分量数量减1
            componentCount--;
        }
        // 如果已经在同一个连通分量中，则无需操作
    }

    /**
     * 查找顶点所在连通分量的根节点（Find操作）
     * 
     * 路径压缩
     * - 在查找过程中，将路径上的所有节点直接指向根节点
     * - 这样可以将树的高度压缩，提高后续查找效率
     * 
     * @param x 要查找的顶点
     * @return 该顶点所在连通分量的根节点
     */
    public T find(T x) {
        // 如果x不是根节点（即father[x] != x）
        if (!x.equals(father.get(x))) {
            // 递归查找根节点，同时进行路径压缩
            // 将x的父节点直接设置为根节点，跳过中间节点
            father.put(x, find(father.get(x)));
        }
        // 返回根节点（可能是x本身，也可能是压缩后的根节点）
        return father.get(x);
    }

    /**
     * 获取当前并查集中连通分量的数量
     * 
     * @return 连通分量数量
     * 时间复杂度：O(1)
     */
    public int getComponentCount() {
        return componentCount;
    }

    /**
     * 判断两个顶点是否在同一个连通分量中
     * 
     * @param u 第一个顶点
     * @param v 第二个顶点
     * @return 如果在同一个连通分量中返回true，否则返回false
     */
    public boolean isConnected(T u, T v) {
        // 通过比较两个顶点的根节点是否相同来判断连通性
        return find(u).equals(find(v));
    }
}

关于路径压缩与按秩合并

直接看解题实操的，可跳过该原理分析部分，点击跳转下一标题：实战秒杀题目

为了防止并查集在极端情况下退化成链表（导致Find操作复杂度变为O(n)），我们通常会采用两种核心优化策略：路径压缩和按秩合并。我们的模板中默认实现了路径压缩，这是最常用也是效果最显著的优化。

1. 路径压缩

路径压缩在find操作中实现，核心思想是：在查找一个节点的根节点时，将查找路径上所有节点都直接指向根节点。这极大地降低了树的高度，使得后续的查找操作变得非常快。

代码对比

路径压缩前的 find 方法：

// 递归查找根节点，但不改变路径上节点的父指针
public T findWithoutCompression(T x) {
    T current = x;
    // 循环直到找到根节点（父节点是自己）
    while (!father.get(current).equals(current)) {
        current = father.get(current);
    }
    return current;
}

缺点：如果树形成一条长链，每次find都需要遍历整条链，时间复杂度为O(n)。

路径压缩后的 find 方法（模板采用）：

// 递归查找根节点，同时将路径上所有节点直接指向根节点
public T find(T x) {
    // 如果x的父节点不是自己，说明它不是根
    if (!father.get(x).equals(x)) {
        // 递归查找根节点，并将x的父节点直接设置为根节点
        father.put(x, find(father.get(x)));
    }
    // 返回根节点
    return father.get(x);
}

优势：一次查找后，树的高度被“压缩”，后续对路径上任一节点的查找都接近O(1)。

图论意义

路径压缩将树的高度显著降低，使得所有非根节点都趋向于直接指向根节点，这样可以：

极致优化查询效率：将find操作的均摊时间复杂度降至O(α(n))。
保持树的“扁平化”：避免了链式结构的出现。
不改变连通性：只改变内部指针，不影响任何节点所属的集合。

2. 按秩合并

按秩合并是在join（或Union）操作中的一种优化策略，目的是在合并两个集合时，总是将“小”的树合并到“大”的树上，以避免树的高度不必要地增加。

按秩（Rank）：基于树的高度。将高度较小的树合并到高度较大的树上。
按大小（Size）：基于集合的节点数。将节点数较少的树合并到节点数较多的树上。（实现更简单，效果同样出色）

虽然我们的模板为了简洁易用没有默认实现按秩合并（仅路径压缩已经足够高效），虽然时间复杂度可能达不到后面分析的近似O(1)，但是综合考量使用方便和性能够用，我们仍按照最佳实践分析。
如文章开头所说，本文并非深入剖析并查集的各个方法的时间复杂度，而是提供一个通用且均衡的**“刷题向”模板**，简化解题思路
不过结合了下方的“按大小合并的join方法实现示例”之后，大家也能轻松实现一个方法时间复杂度均接近 O(1) 的并查集模板

（补充内容，可跳过，直接看使用）下面是按大小合并的join方法实现示例：

// 需要额外一个Map来存储每个集合的大小
private final Map<T, Integer> size = new HashMap<>();

// 在add(x)时，初始化size.put(x, 1);

public void join(T u, T v) {
    add(u); add(v);
    T rootU = find(u);
    T rootV = find(v);
    if (!rootU.equals(rootV)) {
        // 按大小合并：将小树合并到大树上
        if (size.get(rootU) < size.get(rootV)) {
            T temp = rootU;
            rootU = rootV;
            rootV = temp;
        }
        // 将v的根合并到u的根上
        father.put(rootV, rootU);
        // 更新合并后集合的大小
        size.put(rootU, size.get(rootU) + size.get(rootV));
        componentCount--;
    }
}

组合效果：同时使用路径压缩和按秩合并，可以证明其时间复杂度为O(α(n))，在实践中近乎为常数时间O(1)，是性能最强的并查集实现。

★实战秒杀案例

借助于上述并查集模板类，我们可以对下列题目进行非常直观的降维打击，稍加分析，使用正常智人思维即可轻松调用 api 解出！

1. 洛谷1551题：亲戚

题目链接：P1551 亲戚 - 洛谷

题目描述

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

规定： a 和 b 是亲戚， b 和 c 是亲戚，那么 a 和 c 也是亲戚。如果 a, b 是亲戚，那么 a 的亲戚都是 b 的亲戚， b 的亲戚也都是 a 的亲戚。

输入格式

第一行：三个整数 n, m, p（1 <= n, m, p <= 5000），分别表示有 n 个人， m 个亲戚关系，询问 p 对亲戚关系。
以下 m 行：每行两个数 Mi, Mj（1 <= Mi, Mj <= n），表示 Mi 和 Mj 具有亲戚关系。
接下来 p 行：每行两个数 Pi, Pj，询问 Pi 和 Pj 是否具有亲戚关系。

输出格式

p 行，每行一个 Yes 或 No。表示第 i 个询问的答案为“具有”或“不具有”亲戚关系。

输入输出样例

输入 #1

输出 #1

Yes
Yes
No

使用并查集思维

这个问题是并查集最直接、最经典的应用，完美诠释了其核心功能。

为什么使用并查集？

传递性：题目中“a和b是亲戚，b和c是亲戚，则a和c也是亲戚”的描述，完美地定义了一种等价关系。并查集正是为了维护这种具有传递性的等价关系而生的。所有在同一个集合中的元素，都满足这种等价关系，将这种关系抽象为图时，构成了一个无向图（众所周知，无向图是可以双向传递的，也就是关系的双向性），所以此刻天然契合使用并查集来秒杀。
高效查询：对于大量的关系建立和存在性查询，并查集提供了近乎O(1)的均摊时间复杂度，远胜于其他如图遍历（每次查询都需要O(N+M)）等方法。

元素抽象：每个人（编号1到n）是并查集中的一个元素。
关系抽象：一个“亲戚关系” (Mi, Mj) 意味着这两个人属于同一个“家族”。在并查集中，这对应着将 Mi 和 Mj 所在的集合进行合并（Union操作）。亲戚关系的传递性（a-b, b-c => a-c）正是通过并查集的合并操作来体现的：当a和b合并，b和c合并后，a, b, c都会在同一个集合中，有同一个根节点。
查询抽象：询问两个人 (Pi, Pj) 是否有亲戚关系，就等价于查询他们是否属于同一个家族，即在并查集中他们是否在同一个集合里（isConnected(Pi, Pj)）。

解题步骤：

初始化：创建并查集，将 n 个人（1到n）分别添加进去，每个人自成一个家族。
建立关系：读取 m 个亲戚关系，对每一对关系 (Mi, Mj)，执行 join(Mi, Mj)，将他们所在的家族合并。
处理查询：读取 p 个查询，对每一对查询 (Pi, Pj)，执行 isConnected(Pi, Pj)。如果返回 true，则输出 Yes；否则输出 No。

题解代码

洛谷、卡码网等刷题不是力扣那样的核心代码模式，需要写Main类和main方法，以及自己导包

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main1551 {
    public static void main(String[] args) throws IOException {
        // 使用“快读”而非Scanner，效率更高
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] split = br.readLine().split("\\s+");
        // n: 人数, m: 关系数, p: 查询数
        int n = Integer.parseInt(split[0]);
        int m = Integer.parseInt(split[1]);
        int p = Integer.parseInt(split[2]);

        // 创建并查集
        DisjointSetUnion<Integer> dsu = new DisjointSetUnion<>();

        // 初始化，将所有n个人添加到并查集中，每个人初始时自成一个家族
        for (int i = 1; i <= n; i++) {
            dsu.add(i);
        }

        // 读取m个亲戚关系，并合并相应的集合
        for (int i = 0; i < m; i++) {
            split = br.readLine().split("\\s+");
            int person1 = Integer.parseInt(split[0]);
            int person2 = Integer.parseInt(split[1]);
            // 合并两个人的家族
            dsu.join(person1, person2);
        }

        // 读取p个查询，并判断他们是否是亲戚
        for (int i = 0; i < p; i++) {
            split = br.readLine().split("\\s+");
            int queryPerson1 = Integer.parseInt(split[0]);
            int queryPerson2 = Integer.parseInt(split[1]);

            // 检查两个人是否在同一个集合中
            if (dsu.isConnected(queryPerson1, queryPerson2)) {
                System.out.println("Yes");
            } else {
                System.out.println("No");
            }
        }
    }
}

基于 洛谷1551 引出的通用变式：

题目：给定 n 个人和 m 对朋友关系，问有多少个朋友圈（连通分量）？

有了上述的理解之后，这题也非常简单明了了，无非以下要点：

将每个人视为并查集中的一个元素/节点。
每对朋友关系视为连接两个元素的边。
朋友圈即为并查集中的一个连通分量/独立集合。

流程简析：

初始化：
创建 n 个独立的集合，每个集合包含一个人。
初始化连通分量计数器 componentCount = n。

处理朋友关系：
对于每对朋友关系 (u, v)：
查找 u 所在集合的代表元素（根）。
查找 v 所在集合的代表元素（根）。
如果 u 和 v 的根不同，说明他们目前不在同一个朋友圈，则将这两个集合合并。
合并后，连通分量计数器 componentCount 减 1。

查找代表元素：
find(x) 方法用于确定元素 x 属于哪个集合。
在查找过程中，执行路径压缩：将 x 及其路径上的所有节点直接连接到它们的最终根节点。这能极大地扁平化树结构，优化后续查询效率。

完整题解：

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); // 人数
        int m = sc.nextInt(); // 朋友关系对数

        // 用人的编号表示人
        DisjointSetUnion<Integer> dsu = new DisjointSetUnion<>();

        for (int i = 1; i <= n; i++) {
            // 初始化人
            dsu.add(i);
        }

        // 录入关系数据
        for (int i = 0; i < m; i++) {
            dsu.join(sc.nextInt(), sc.nextInt());
        }

        // 调 API，输出该并查集中有几个连通分量（由于使用了路径压缩，所以相当于找有几个根即可）
        System.out.println(dsu.getComponentCount());
    }
}

2. 卡码107题：寻找存在的路径

题目链接：107. 寻找存在的路径 (kamacoder.com)

题目描述

给定一个包含 n 个节点的无向图中，节点编号从 1 到 n （含 1 和 n ）。你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。

输入描述

第一行包含两个正整数 N 和 M，N 代表节点的个数，M 代表边的个数。
后续 M 行，每行两个正整数 s 和 t，代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数，代表起始节点 source 和目标节点 destination。

输出描述

输出一个整数，代表是否存在从节点 source 到节点 destination 的路径。如果存在，输出 1；否则，输出 0。

输入示例

输出示例

使用并查集思维

这个问题本质上是判断图中的两个点是否连通。这正是并查集的经典应用场景。

节点抽象：图中的每个节点（编号1到n）都可以看作是并查集中的一个元素。
边的抽象：图中的每一条边 (u, v) 都意味着节点 u 和 v 是连通的。在并查集中，这对应着将 u 和 v 所在的集合进行合并（Union操作）。
路径存在性判断：判断从 source 到 destination 是否存在路径，就等价于判断 source 和 destination 是否在同一个连通分量中。在并查集中，这对应着检查 source 和 destination 是否有共同的根节点（Find操作）。

通过处理所有的边，我们将所有直接或间接相连的节点都合并到同一个集合中。最后，只需要一次查询即可判断任意两点间的连通性。

题解代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    public static void main(String[] args) throws IOException {
        // 比Scanner高效的“快读”法
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        // 读取节点数N和边数M
        String[] split = br.readLine().split("\\s+");
        int n = Integer.parseInt(split[0]);
        int m = Integer.parseInt(split[1]);

        // 实例化并查集，Integer有默认的equals和hashCode，无需我们手动实现
        DisjointSetUnion<Integer> dsu = new DisjointSetUnion<>();
        // 初始化，将1到n的每个节点都作为一个独立的集合添加到并查集中
        for (int i = 1; i <= n; i++) {
            dsu.add(i);
        }

        // 遍历所有边
        for (int i = 0; i < m; i++) {
            split = br.readLine().split("\\s");
            // 读取边的两个端点
            int u = Integer.parseInt(split[0]);
            int v = Integer.parseInt(split[1]);
            // 合并这两个端点所在的集合，表示它们是连通的
            dsu.join(u, v);
        }

        // 读取源节点和目标节点
        split = br.readLine().split("\\s");
        int source = Integer.parseInt(split[0]);
        int destination = Integer.parseInt(split[1]);

        // 判断源和目标是否在同一个集合中
        // 如果是，则路径存在，输出1；否则输出0
        System.out.println(
        	dsu.isConnected(source, destination) ? 1 : 0
        );
    }
}

3. 力扣200题：岛屿数量

题目链接：200. 岛屿数量 - 力扣（LeetCode）

题目描述

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

使用并查集思维

这个问题可以转化为计算图中连通分量的数量。

节点抽象：网格中的每一块陆地（值为 '1' 的格子）都可以看作是图中的一个节点。
边的抽象：如果两块陆地在水平或垂直方向上相邻，那么它们之间就存在一条边，表示它们是连通的。
岛屿计数：一个岛屿就是由所有相互连接的陆地格子组成的集合。因此，岛屿的数量就等于图中连通分量的数量。

解题步骤：

初始化：创建一个并查集。初始时，连通分量的数量为0。
遍历网格：遍历二维网格中的每个格子。
处理陆地：当遇到一个陆地格子 (i, j) 时：
- 首先，将这个陆地格子自身视为一个独立的连通分量（如果它尚未被添加），并查集中的连通分量总数加1。
- 然后，检查它的上方和左方（或下方和右方，选择两个方向即可避免重复）的相邻格子。如果相邻格子也是陆地，就将当前陆地格子与相邻陆地格子在并查集中进行合并（Union操作）。如果合并成功（即它们原本不属于同一个连通分量），则并查集中的连通分量总数减1。
返回结果：遍历完整个网格后，并查集中维护的连通分量数量就是最终的岛屿数量。

技巧优化：为了在并查集中唯一标识每个格子，需要将二维坐标 (i, j) 映射到一个一维的整数ID，例如 id = i * m + j（其中 m 是网格的列数）。

题解代码

public class Solution {
    // 并查集实例，用于维护陆地格子的连通关系
    DisjointSetUnion<Integer> dsu;
    // 网格的行数和列数
    int n, m;

    /**
     * 主函数，计算岛屿数量
     * @param grid 二维网格，'1'为陆地，'0'为水
     * @return 岛屿数量
     */
    public int numIslands(char[][] grid) {
        dsu = new DisjointSetUnion<>();
        n = grid.length;
        m = grid[0].length;

        // 遍历网格中的每个格子
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                // 如果当前格子是陆地
                if (grid[i][j] == '1') {
                    // 将当前陆地格子添加到并查集中，如果它不存在，连通分量数会加1
                    dsu.add(calId(i, j));
                    // 检查并合并相邻的陆地
                    // 只检查下方和右方，避免重复检查
                    // 检查下方
                    if (i + 1 < n && grid[i + 1][j] == '1') {
                        dsu.join(calId(i, j), calId(i + 1, j));
                    }
                    // 检查右方
                    if (j + 1 < m && grid[i][j + 1] == '1') {
                        dsu.join(calId(i, j), calId(i, j + 1));
                    }
                }
            }
        }

        // 最终并查集中的连通分量数量即为岛屿数量
        return dsu.getComponentCount();
    }

    /**
     * 将二维坐标 (i, j) 转换为一维的唯一ID
     * @param i 行坐标
     * @param j 列坐标
     * @return 唯一ID
     */
    public int calId(int i, int j) {
        return i * m + j;
    }
}

注：该题使用 dfs 也同样简单直观 ↓

public class Solution {
    static int n, m, ans;
    static boolean[][] visited;

    // 普通dfs解法
    public int numIslands(char[][] grid) {
        n = grid.length;
        m = grid[0].length;

        visited = new boolean[n][m];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (!visited[i][j] && grid[i][j] == '1') {
                    ans++;
                    dfs(grid, i, j);
                }
            }
        }
        return ans;
    }

    // 计算岛屿数量
    public static void dfs(char[][] grid, int i, int j) {
        if (i < 0 || i >= n || j < 0 || j >= m || visited[i][j] || grid[i][j] != '1') {
            return;
        }

        visited[i][j] = true;

        dfs(grid, i - 1, j);
        dfs(grid, i + 1, j);
        dfs(grid, i, j - 1);
        dfs(grid, i, j + 1);
    }
}

4. 力扣547题：省份数量

题目链接：547. 省份数量 - 力扣（LeetCode）

题目描述

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i] [j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i] [j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例 1

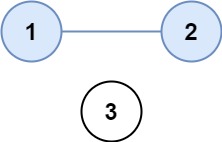
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2

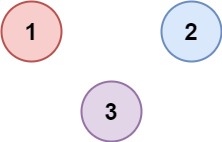
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

使用并查集思维

这个问题是“岛屿数量”问题的变体，同样是计算图的连通分量数量。

与dfs/bfs对比：

dfs/bfs：通过遍历找到一个未访问的城市，然后深入或广度优先地访问所有与之相连的城市，并标记为已访问。每启动一次新的遍历，就意味着发现了一个新的省份。这种方法直观，易于理解。
并查集：将每个城市视为一个独立的集合。遍历邻接关系，不断合并属于同一省份的城市。最后统计集合的数量。并查集的优势在于其“合并”操作的效率极高，对于处理动态连通性问题或关系合并非常有效。对于本题，两种方法复杂度相似，但并查集提供了一个不同的、基于“集合”的视角。

节点抽象：每个城市（编号从 0 到 n-1）是图中的一个节点，对应并查集中的一个元素。
边的抽象：邻接矩阵 isConnected[i][j] = 1 表示城市 i 和城市 j 之间有一条直接连接的边。这对应于在并查集中合并 i 和 j。
省份计数：一个“省份”就是图中的一个连通分量。因此，省份的数量就是最终并查集中集合的数量。

解题步骤：

初始化：创建一个并查集，并将 n 个城市（0 到 n-1）分别作为独立的集合添加进去。此时，连通分量（省份）的数量为 n。
遍历邻接矩阵：遍历 isConnected 矩阵的上半部分（因为 isConnected[i][j] == isConnected[j][i]，遍历一半即可）。
合并城市：当发现 isConnected[i][j] == 1 时，表示城市 i 和 j 直接相连。此时，在并查集中执行 join(i, j) 操作。如果 i 和 j 原本不属于同一个省份，合并后省份总数会减1。
返回结果：遍历完整个邻接矩阵后，并查集中剩余的连通分量数量就是省份的总数。

题解代码

public class Solution {
    /**
     * 计算省份数量
     * @param isConnected 邻接矩阵，表示城市间的连接关系
     * @return 省份数量
     */
    public int findCircleNum(int[][] isConnected) {
        // 城市数量
        int n = isConnected.length;
        // 实例化并查集
        DisjointSetUnion<Integer> dsu = new DisjointSetUnion<>();

        // 初始化，每个城市最初都是一个独立的省份
        for (int i = 0; i < n; i++) {
            dsu.add(i);
        }

        // 遍历邻接矩阵的上半部分来建立连接关系
        for (int i = 0; i < n; i++) {
            // j从i+1开始，避免重复遍历和处理对角线
            for (int j = i + 1; j < n; j++) {
                // 如果两个城市直接相连
                if (isConnected[i][j] == 1) {
                    // 则将它们合并到同一个省份（集合）中
                    dsu.join(i, j);
                }
            }
        }

        // 最终的连通分量数就是省份数
        return dsu.getComponentCount();
    }
}

此题的dfs，bfs解法代码略

5. 力扣684题：冗余连接

题目链接：684. 冗余连接 - 力扣（LeetCode）

题目描述

树可以看成是一个连通且无环的无向图。

给定一个图，该图从一棵 n 个节点 (节点值 1～n) 的树中添加一条边后获得。添加的边的两个不同顶点编号在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1

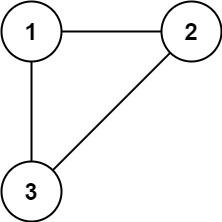
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2

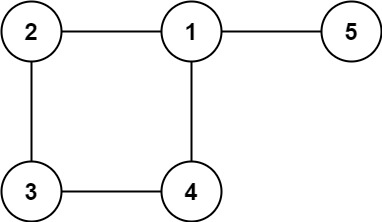
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

使用并查集思维

这个问题的核心是在图中检测环。一条边之所以“冗余”，是因为它连接了两个本就已经连通的节点，从而形成了一个环。

解题思路深度剖析：

树的特性：一棵包含n个节点的树，有且仅有n-1条边，并且图中无环。
冗余边的本质：当一个图有n个节点和n条边时，它必然包含至少一个环。这条导致成环的“多余”的边就是冗余连接。
并查集的作用：并查集是检测环的利器。当我们遍历边列表，尝试将边的两个端点u和v加入集合时，如果u和v在加入前就已经属于同一个集合（isConnected(u,v)为true），说明图中已经存在一条从u到v的路径。此时再加入边(u,v)，就会形成一个闭合的环路。因此，这条边就是冗-余的。

节点抽象：图中的每个节点（1到n）是并查集中的一个元素。
边的处理：我们按顺序遍历 edges 数组中的每一条边 (u, v)。
环的检测：在处理边 (u, v) 之前，我们先用并查集检查 u 和 v 是否已经连通（即 isConnected(u, v)）。
- 如果 u 和 v 已经连通：说明在 u 和 v 之间已经存在一条路径。此时再加入边 (u, v)，必然会形成一个环。因此，这条边 (u, v) 就是我们要找的冗余连接。
- 如果 u 和 v 尚未连通：说明这条边是连接两个不同连通分量的“桥”，不会形成环。我们应该将它加入图中，即在并查集中执行 join(u, v) 操作。

因为题目要求返回最后出现的冗余边，所以我们只需按顺序遍历，找到的第一条导致成环的边就是答案（如果有多条，最后一条被判断为冗余的边会覆盖前面的结果）。

题解代码

public class Solution {
    /**
     * 寻找冗余连接
     * @param edges 图的边列表
     * @return 导致成环的冗余边
     */
    public int[] findRedundantConnection(int[][] edges) {
        // 实例化并查集
        DisjointSetUnion<Integer> dsu = new DisjointSetUnion<>();

        // 遍历每一条边
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];

            // 在处理这条边之前，检查它的两个端点是否已经连通
            // 注意：我们的模板在join时会自动add节点，所以这里可以不显式调用add
            if (dsu.isConnected(u, v)) {
                // 如果已经连通，说明添加这条边会形成环
                // 因此，这条边就是冗余的
                // 根据题意，返回最后出现的冗余边，所以直接返回当前边即可
                return edge;
            } else {
                // 如果不连通，则这是一条有效的树边，将它们合并
                dsu.join(u, v);
            }
        }

        // 根据题目保证，一定存在冗余连接，所以理论上不会执行到这里
        return new int[0];
    }
}

题目对比分析表

题目	问题类型	核心操作	关键技巧	时间复杂度	空间复杂度
洛谷1551	关系查询	isConnected	传递性关系建模	O((m+p)·α(n)) (近乎O(m+p))	O(n)
卡码107	路径存在性	isConnected	预初始化所有节点	O(m·α(n)) (近乎O(m))	O(n)
LC200	连通分量计数	getComponentCount	二维坐标映射	O(mn·α(mn)) (近乎O(mn))	O(mn)
LC547	连通分量计数	getComponentCount	矩阵对称性优化	O(n²·α(n)) (近乎O(n²))	O(n)
LC684	环检测	isConnected + join	添加前检查连通性	O(n·α(n)) (近乎O(n))	O(n)

共性特征分析

1. 问题本质

所有题目的核心都是图的连通性问题：

静态查询：判断两点是否连通（卡码107、洛谷1551）
动态计数：统计连通分量数量（LC200、LC547）
环检测：检测边的添加是否形成环（LC684）

2. 数据结构选择

所有题目都选择并查集的原因：

当然并不代表其他解法，如：dfs 等行不通，相反，在有些题目中 dfs 反而更加高效，例如力扣200；只不过使用模板更加无脑简单，如上述所有代码逻辑，无需复杂递归设计，只需宏观上将问题向“连通分量”、“连通性”等方向思考、转移即可。

高效合并：O(α(n)) 时间复杂度合并两个集合
快速查询：O(α(n)) 时间复杂度判断连通性
实时维护：动态维护连通分量信息

3. 算法模式

1. 初始化并查集
2. 处理连接关系（边）
3. 执行查询操作

使用技巧与优化策略

上述几题中，有些使用了一些技巧或优化，经过这些技巧的转换，让使用并查集变得更加自然且流畅

1. 坐标转换技巧

适用场景：二维网格问题（如LC200）

// 将二维坐标(i,j)转换为一维唯一ID（类似取 hashCode 的思想，方式非唯一）
int id = i * cols + j;

优势：

避免使用复杂的二维坐标作为键
提高HashMap的查找效率
节省内存空间

2. 矩阵对称性优化

适用场景：邻接矩阵表示的无向图（如LC547）

// 只遍历上三角矩阵
for (int i = 0; i < n; i++) {
    for (int j = i + 1; j < n; j++) {
        // 处理边(i,j)
    }
}

优势：

减少一半的遍历次数
避免重复处理同一条边

3. 提前退出优化

适用场景：当达到特定条件时可以提前结束（如LC547）

if (dsu.getComponentCount() == 1) {
    return 1; // 所有节点已连通
}

优势：

在最优情况下显著提升性能
避免不必要的计算

4. 环检测模式

适用场景：需要检测图中环的存在（如LC684）

if (dsu.isConnected(u, v)) {
    // 添加边(u,v)会形成环
    return edge;
} else {
    dsu.join(u, v);
}

优势：

实时检测环的形成
避免构建完整图后再检测

5. 预初始化策略

适用场景：节点数量已知的情况（如卡码107、洛谷1551）

// 预先添加所有节点
for (int i = 1; i <= n; i++) {
    dsu.add(i);
}

优势：

避免join操作中的重复检查
提高代码的可读性和性能

时间复杂度深度分析

阿克曼函数与反阿克曼函数 α(n)

这是什么?

阿克曼函数：一个增长速度极快的递归函数，它的值增长速度远超指数、阶乘等任何我们熟知的函数。对于很小的输入，其输出就大到无法想象。
反阿克曼函数 α(n)：阿克曼函数的反函数，因此它的增长速度极其缓慢。

和并查集有什么关系?
经过路径压缩和按秩合并优化的并查集，其find和join操作的平均时间复杂度被证明为 O(α(n))，参考：并查集复杂度 - OI Wiki (oi-wiki.org)

为什么可以近似看作 O(1)?
因为 α(n) 的增长实在是太慢了。在计算机科学能处理的任何问题规模 n 中（例如，n 小于宇宙中所有原子的数量），α(n) 的值都不会超过 5。因此，在实践中，我们可以放心地将其视为一个极小的常数，时间复杂度近似为 O(1)。

相关知识链接:

阿克曼函数详解 (优快云博客)
并查集复杂度与反阿克曼函数 (博客园)
https://blog.youkuaiyun.com/lemonoil/article/details/57085830

各操作复杂度

操作	未优化	仅路径压缩	仅按秩合并	路径压缩 + 按秩合并
`find`	O(n)	O(log n)	O(log n)	O(α(n)) (近乎O(1))
`join`	O(n)	O(log n)	O(log n)	O(α(n)) (近乎O(1))
`isConnected`	O(n)	O(log n)	O(log n)	O(α(n)) (近乎O(1))
`getComponentCount`	O(1)	O(1)	O(1)	O(1) 直接返回计数器

并查集的适用场景

适合使用并查集的问题

动态连通性查询：需要频繁查询两点是否连通
连通分量计数：需要实时维护连通分量数量
环检测：在图的构建过程中检测环
等价关系处理：处理具有传递性的关系
最小生成树算法：Kruskal算法的核心组件

不适合使用并查集的问题

路径查询：需要找到两点间的具体路径
最短路径：需要计算两点间的最短距离
图的遍历：需要按特定顺序访问节点
动态删除边：并查集不支持高效的边删除

总结与扩充

模板优势

通用性强：泛型设计，支持任意类型元素；刷题中一般 int 多见
性能卓越：路径压缩优化，接近 O(1) 操作
功能完整：提供连通分量计数等高级功能
易于使用：API简洁，学习成本低；上手直接无脑手戳，或者Ctrl C V大法再说

实际应用价值

算法竞赛：快速解决连通性相关问题
系统设计：网络连通性检测、用户关系分析
数据处理：大规模数据的分组和聚类
图算法：作为其他复杂图算法的基础组件

在刷题过程中，遇到连通性问题时，可以直接使用这个模板，大大提高解题效率。
特别适用于图论中的连通分量、最小生成树、动态连通性等问题。掌握并查集不仅能解决特定类型的题目，更能加深对图论和数据结构的理解。

但是注意：

dfs+递归等老方法固然是基本功，需要完全掌握，但是并查集的解法更算是一种进阶解法，某些情况下极其好用。
不要为了使用模板而使用模板，有时候借助显然的递归反而能更加轻松且高效解题，以免南辕北辙。

模板性能极致优化

虽然我们提供的泛型模板通用性强且足够高效，但在对性能要求极为苛刻的场景（如算法竞赛），还可以进行以下优化：

1. 移除健壮性检查

模板中的add方法包含了father.containsKey(x)检查，以防止重复添加和保证程序的健壮性。但在竞赛中，通常可以确保输入数据的有效性（例如，节点编号在给定范围内且不重复）。此时，可以移除这些检查，由调用者自己保证初始化的正确性，从而省去一部分哈希查找的开销。

2. 使用数组替代HashMap

当并查集处理的元素是从0或1开始的连续整数时，使用数组是比HashMap更高效的选择。这可以完全避免HashMap的哈希计算开销以及泛型带来的装箱/拆箱成本。

HashMap 底层虽然也是数组实现，但是当 HashMap 的底层数组达到一定程度的时候，会进行扩容，这将一定程度上降低效率。（参考：关于HashMap扩容）

但是对于大部分的网站刷题来说，使用上述模板已经足够了。

3. 实现按秩/大小合并进一步优化模板

参考“路径压缩”与“按秩/大小合并”优化算法时间复杂度：按秩/大小合并

数组实现等价模板：

/**
 * 并查集模板类（数组实现）
 * 适用于元素是连续整数（如 0 到 n-1）的场景
 */
public class DisjointSetUnionInt {
    // 存储父节点的数组，father[i]表示i的父节点
    private int[] father;
    // 连通分量的数量
    private int componentCount;

    /**
     * 构造函数
     * @param n 元素总数（编号从0到n-1）
     */
    public DisjointSetUnionInt(int n) {
        father = new int[n];
        this.componentCount = n;
        // 初始化，每个元素的父节点都是自己
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
    }

    /**
     * 查找元素i所在集合的根节点（带路径压缩）
     */
    public int find(int i) {
        if (father[i] != i) {
            father[i] = find(father[i]); // 路径压缩
        }
        return father[i];
    }

    /**
     * 合并元素i和j所在的集合
     */
    public void join(int i, int j) {
        i= find(i);
        j = find(j);
        if (i!= j) {
            father[j] = i; // 将j的根指向i的根
            componentCount--;
        }
    }

    /**
     * 判断两个元素是否在同一个集合中
     */
    public boolean isConnected(int i, int j) {
        return find(i) == find(j);
    }

    /**
     * 获取当前连通分量的数量
     */
    public int getComponentCount() {
        return componentCount;
    }
}

泛型模板 vs 数组模板

核心思想一致：无论是泛型模板还是数组模板，其底层实现的并查集原理是完全等价的。

它们都依赖于father数据结构来维护父子关系，并通过find（路径压缩）和join操作来管理集合。区别仅在于数据存储方式和适用场景。

	泛型模板 (DisjointSetUnion)	数组模板 (DisjointSetUnionInt)
通用性	极高。支持任何对象类型（字符串、自定义类等），只要正确实现`equals`和`hashCode`。	有限。仅适用于从0或1开始的连续整数。
性能	高。但有`HashMap`的哈希计算和泛型装箱/拆箱的开销。	极致。直接进行数组索引，无任何额外开销。
内存开销	较大。`HashMap`需要存储键、值、哈希码和链表/红黑树指针。	较小。仅需一个`int`数组的内存空间。
初始化	动态。可以随时通过 add 或 join 方法加入新元素，无需预先知道总数。	静态。需要预先知道元素总数 n，一次性分配所有内存。
选择建议	- 首选：当处理非整数、离散或未知范围的元素时。 - 便利性：代码更灵活，无需手动进行元素到索引的映射	- 首选：在性能要求极高的竞赛或场景中，且元素是连续整数。 - 效率：追求极致的运行速度和最小的内存占用。