代码
#include <iostream>
using namespace std;
typedef long long int LL;
int main() {
LL c[21] = {0};
LL m;
int n;
//求每组(以首元素分组)中的元素个数c[n]
for(int i=1; i<21; i++) {
c[i] = c[i-1]*(i-1)+1;
}
//long long int型用%lld输入
while(scanf("%d%lld", &n, &m)!=EOF) {
int num[21];
for(int i=0; i<21; i++) {
num[i] = i;
}
while(n>0 && m>0) { //n>0的控制是因为最多输出n个数,m>0的控制是因为可能输出的数字个数小于n
//求出所在第几组
int group = m/c[n]+(m%c[n]>0?1:0);
//先输出该数字
cout<<num[group];
//把该数字去除,后面的统一前移
for(int i=group; i<=n; i++) {
num[i] = num[i+1];
}
//把前面group-1组的元素去除,还要去除一个空集
m = m-((group-1)*c[n]+1);
if(m) {//m>0表明后面还有元素,否则没有元素,输出回车
cout<<" ";
} else {
cout<<endl;
}
n--;
}
}
return 0;
}
注解
1、会用typedef简化书写。
2、设f(n)是n个数组成的序列总数,g(n)是每组的个数(首个字符相同即为同一组)。所以f(n)=n(f(n-1)+1),g(n)=f(n)/n=f(n-1)+1。
同理,g(n-1)=f(n-1)/(n-1),所以f(n-1)=(n-1)*g(n-1),所以g(n)=(n-1)*g(n-1)+1。根据此式,可求出每组包含的序列个数,用c[n]表示。
3、读入n和m,m用long long int型,是%lld。首先先把数字归位,即num[i]=i。下面是循环体,循环结束条件是n<=0或者m<=0。n<=0或m<=0时表明该情况下,数字已经输出完了。
4、输出的过程如下:先计算属于第几组,然后把该位置的数字输出,其余数字前移。然后减去前面组的总个数,以及该组的第一个(空集),如此循环下去。
结果






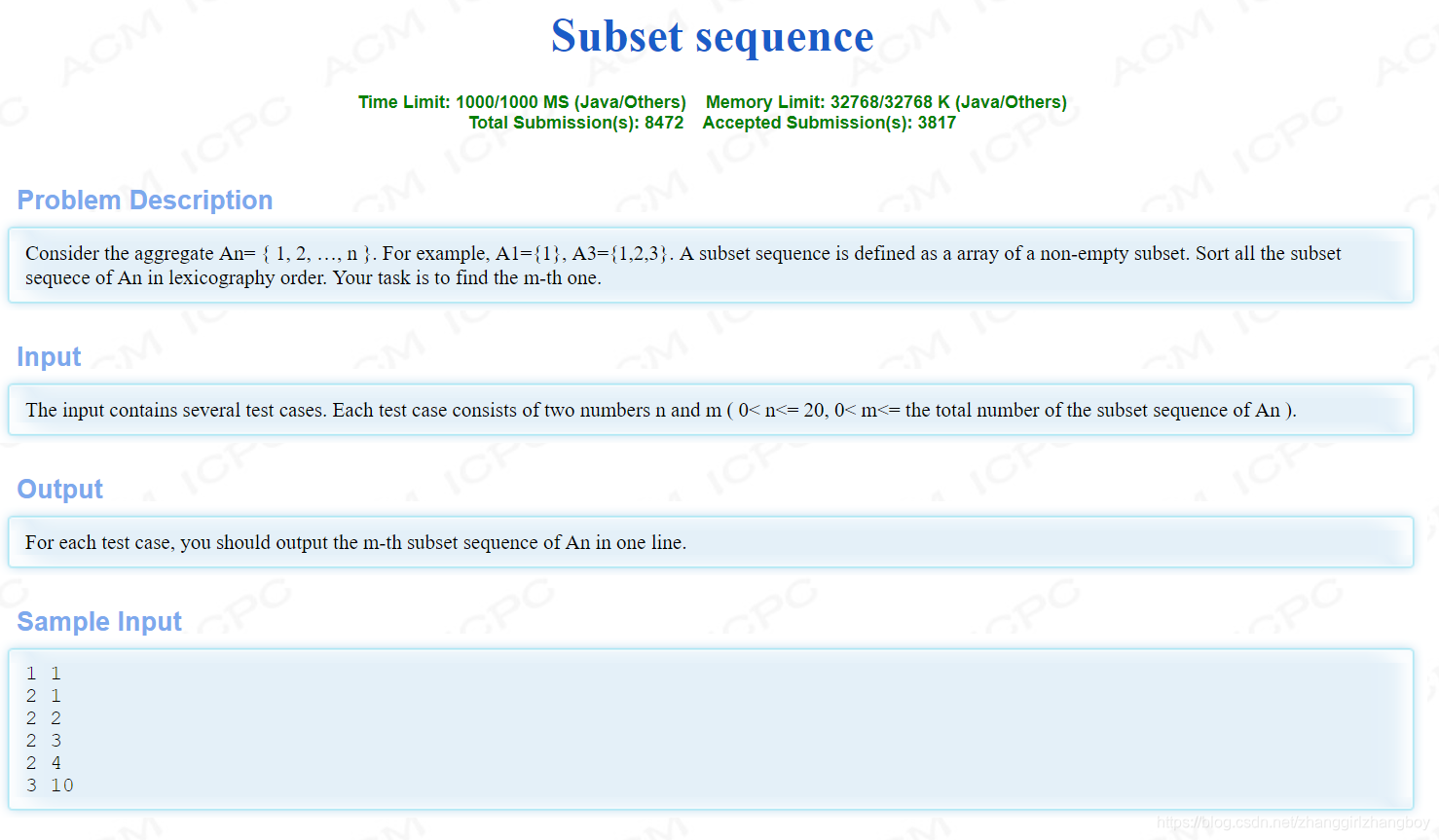
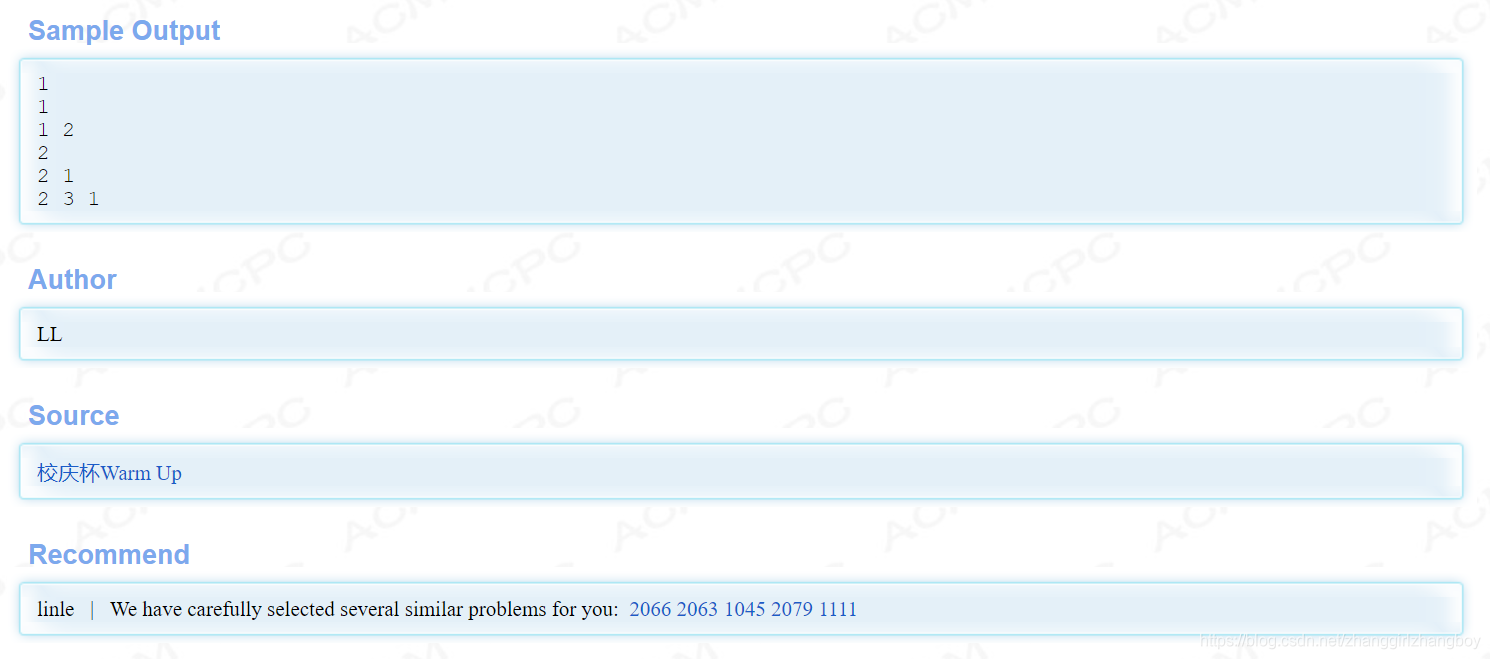
 本文深入探讨了使用C++实现的一种序列生成算法,通过计算特定序列的个数并输出指定序列,展示了typedef的使用、长整型变量的输入方法以及序列生成的逻辑。文章详细解释了序列总数和每组序列数的计算公式,并提供了完整的代码实现。
本文深入探讨了使用C++实现的一种序列生成算法,通过计算特定序列的个数并输出指定序列,展示了typedef的使用、长整型变量的输入方法以及序列生成的逻辑。文章详细解释了序列总数和每组序列数的计算公式,并提供了完整的代码实现。
















 298
298

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








