HDU-2059 龟兔赛跑

最新推荐文章于 2023-03-30 19:30:41 发布

springflower02

最新推荐文章于 2023-03-30 19:30:41 发布

阅读量135

点赞数

CC 4.0 BY-SA版权

分类专栏： hdu 文章标签：动态规划依次将每个站点当作最后一次加油的

本文链接：https://blog.youkuaiyun.com/zhanggirlzhangboy/article/details/85047095

hdu 专栏收录该内容

333 篇文章

订阅专栏

本文介绍了一种使用动态规划算法解决电动车加油策略的问题。通过将起点和终点视为加油站，利用N+2个加油站的位置信息，计算到达每个加油站的最短时间。算法首先初始化起点时间，随后进行动态规划，计算从任意加油站出发到下一加油站的最短时间，最终比较电动车直接行驶和采用最优加油策略的时间，决定胜负。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

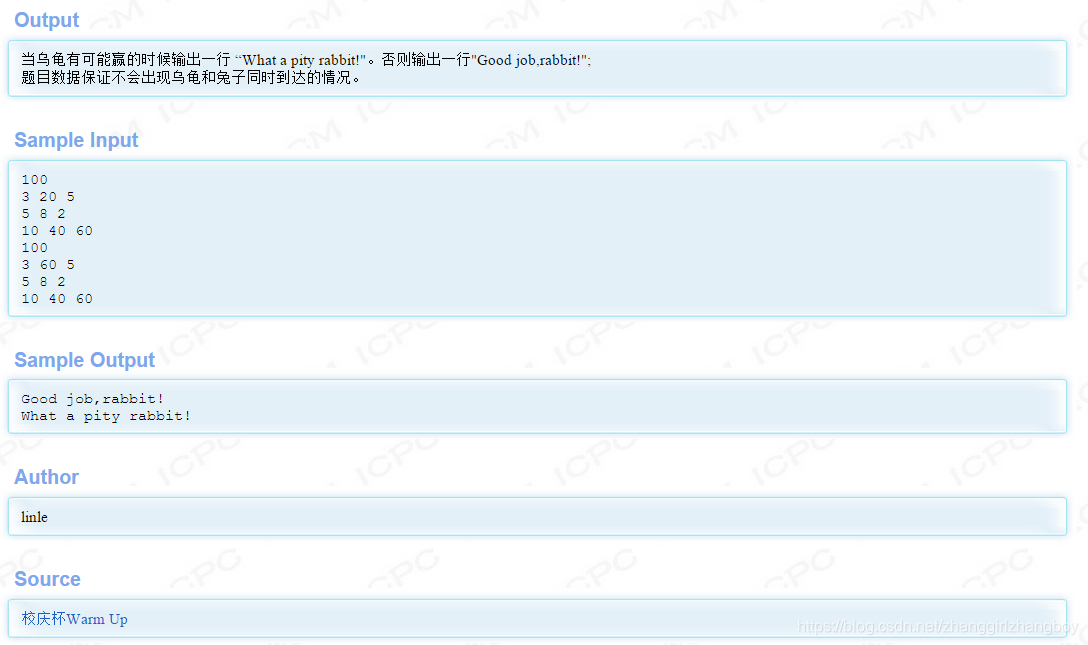
在这里插入图片描述

代码

#include <iostream>

using namespace std;

int main() {

    double L;
    while(cin>>L) {
        int N;
        double C, T;
        cin>>N>>C>>T;
        double VR, VT1, VT2;
        cin>>VR>>VT1>>VT2;

        int dis[N+2];
        dis[0] = 0;
        dis[N+1] = L;
        for(int i=1; i<N+1; i++) {
            cin>>dis[i];
        }

        //init
        double time[N+2];
        time[0] = 0;
        for(int i=1; i<N+2; i++) {
            if(dis[i]>C) {
                double tmpTime = C/VT1 + (dis[i]-C)/VT2;
                time[i] = tmpTime;
            } else {
                double tmpTime = dis[i]/VT1;
                time[i] = tmpTime;
            }
        }

        //dp
        for(int i=1; i<N+1; i++) {
            for(int j=i+1; j<N+2; j++) {
                double tmpTime;
                if(dis[j]-dis[i]>C) {
                    tmpTime = T + C/VT1 + (dis[j]-dis[i]-C)/VT2;
                } else {
                    tmpTime = T + (dis[j]-dis[i])/VT1;
                }
                time[j] = min(time[j], time[i]+tmpTime);
            }
        }

        double rabbit = L/VR;
        if(time[N+1]>rabbit) {
            cout<<"Good job,rabbit!"<<endl;
        } else {
            cout<<"What a pity rabbit!"<<endl;
        }

    }
    return 0;
}

注解

1、简单的动态规划问题。
2、把起点和终点也当作加油站，即有N+2个加油站。用dis数组记录每个加油站离起始点的距离。用time数组记录到每个加油站的最短时间。
3、首先初始化time，也就是把距离起始点为0的加油站当作最后一次加油。然后依次计算每个time。
4、下面开始动态规划：每次把dis[i]当作是最后一次加油，依次计算time[j]所需的最短时间，j>i。time[j]=min(time[j], time[i]+tmpTime)。其中tmpTime表示从上一次加满油到此站点所花的时间。
5、在具体计算tmpTime时间时，需要分两种情况讨论：
（1）从上次加满油到此位置，油已用完，需要有一段时间脚蹬电动车。
（2）从上次加满油到此位置，油还没用完，不需要脚蹬电动车。

结果

在这里插入图片描述