2020牛客暑期多校训练营Tournament(构造)

最新推荐文章于 2024-08-14 23:53:53 发布
原创 最新推荐文章于 2024-08-14 23:53:53 发布 · 423 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#构造

本文探讨了一种优化比赛调度的方法，旨在最小化所有参赛队伍在场地停留的总时间。通过将队伍分为两组并采用特定的配对策略，实现了均衡分配比赛时间的目标。

Tournament

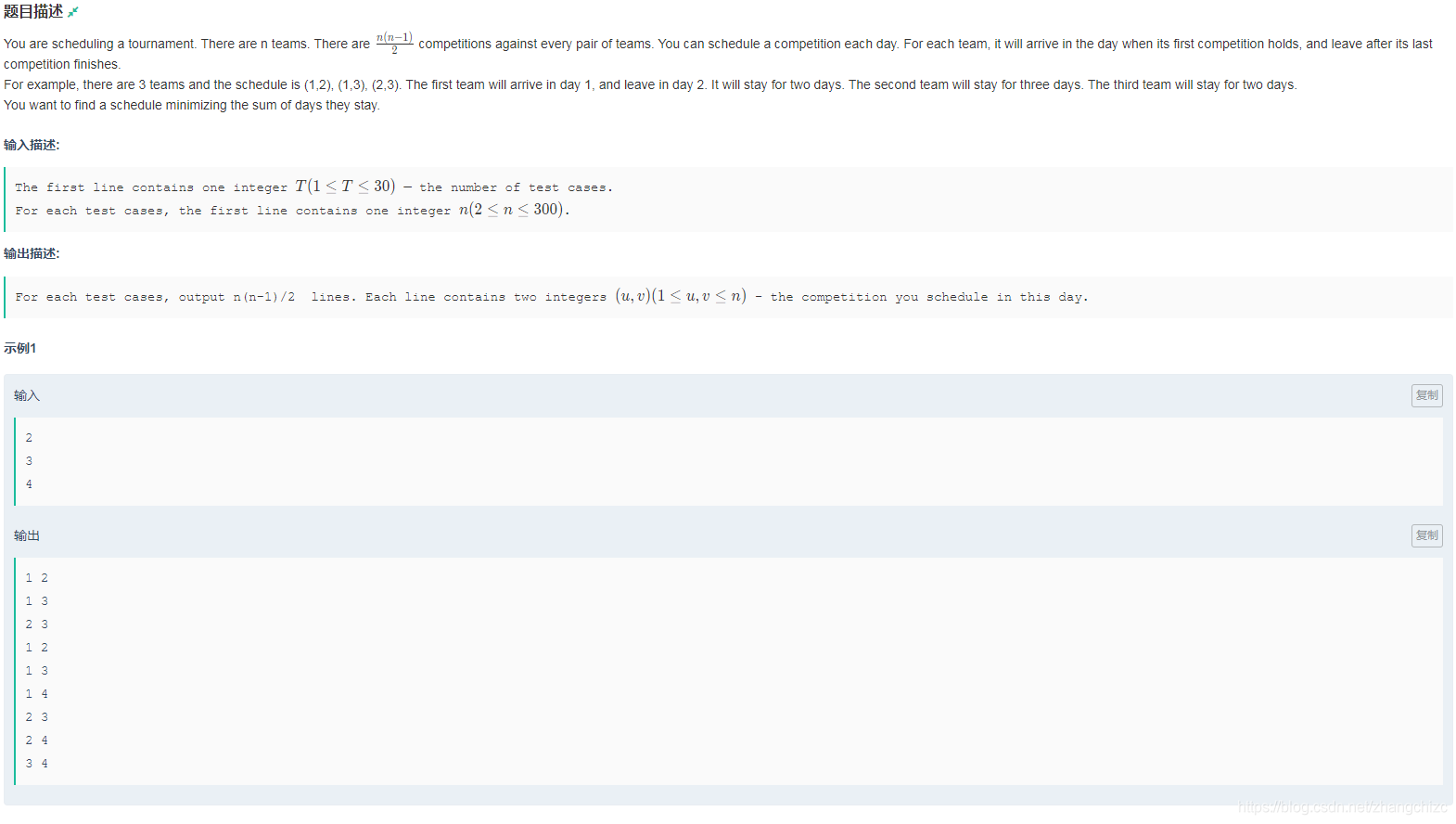
题目描述

在这里插入图片描述

样例

input:
2
3
4
output:
1 2
1 3
2 3
1 2
1 3
1 4
2 3
2 4
3 4

题目大意

有 n n n支队伍两两之间比赛一场，则进行 n ( n − 2 ) 2 \frac{n(n-2)}{2} 2n(n−2)​场。现每支队伍会从他们要比赛的第一天开始直到他们的比赛的最后一场为止，即安排中他们队伍最后出现的那天为止，都会待在比赛场地里。
现你可以安排比赛顺序，要求如何安排会使得所有队伍待在场地里的时间总合最小。

分析

首先想到的是：
f o r ( i    f r o m    1 → n ) for(i\,\,from\,\,1\to n) for(ifrom1→n)
f o r ( j    f r o m    i + 1 → n ) \qquad for(j\,\,from\,\,i+1\to n) for(j

最低0.47元/天 解锁文章
2024牛客暑期多校训练营1 A题（A Bit Common ）解题思路
Wzh20060111的博客
07-17 796
前言：今年和队友报了牛客暑期多校比赛，写了一下午结果除了签到题之外只写出了一道题（A），签到题没什么好说的，其他题我也没什么好说的（太菜了，根本写不出来），这道题能经过自己推导写出公式其实也蛮有成就感的。
2024牛客暑期多校训练营9 补题 B|C
最新发布
2201_75347307的博客
08-14 901
但是对于这种数学问题，挺经常想对于一个行或列去操作，其实是对他的因子操作。否则还要维护最大的标记，最小的标记等等，太繁琐了。然后记得每次标记一个集合的时候，把上一个和这个数相同的标记的集合的影响给消去。每个区间内相同的个数不存在于集合 S 中，问有多少种选择区间的方案。那其实我们可以将矩阵分层，就是每个因子都去建一个矩阵。的矩阵，显然这个的空间复杂度是调和级数的。这个因子，我们看他对答案贡献的个数乘以欧拉函数即可。那么对于一行和列的修改，我们就可以放到每个因子的。，公式的推导详细可能是和卷积有概念。
牛客多校10 - Tournament(找规律)
Falcon的博客
08-11 1614
题目链接：点击查看 题目大意：现在有 n 个队伍参加比赛，任意两个队伍之间都要进行一次比赛，也就是共需要进行 n * ( n - 1 ) / 2 次比赛，对于每个队伍来说，必须要在第一场比赛的时候到达赛场，在最后一场比赛结束后离开赛场，在赛场上呆的时间即为贡献，现在求出一种比赛的安排顺序，使得每个队伍的贡献之和最小 题目分析：可以自己手玩一下找找规律，这里以 n = 6 为例，画个图： 上图中表示了 n * ( n - 1 ) / 2 场比赛按照升序排列后，也就是按照红色箭头的方向依次比赛，相信肯
2020牛客多校第十场I-Tournament
ding_ning123的博客
08-10 445
Decription Solution 首先，看到这题会有一种冲动 怎么办！ 问题在于，我们让第一个人尽快离开，其他人等了很久 我们把它拆成四部分 记住最优宗旨要让所有人尽量一块一块地出现 Case 1 前1→n21 \rightarrow \cfrac{n}{2}1→2n​个人互相比 要让所有人尽量一块一块地出现 For instance,n=10 premulationpremulationpremulation 121\qquad212 131\qquad313 232\q
2020牛客暑期多校训练营（第十场） Tournament
bbbll123的博客
08-10 1467
题目描述 您正在安排比赛。有nnn个球队。 每一对球队有n(n−1)2\frac{n(n-1)}{2}2n(n−1)​个比赛。 每天安排一场比赛。 对于每支球队，它将在第一场比赛举行的当天到达，并在最后一场比赛结束后离开。 例如，有3个团队，日程表是(1，2)(1，2)(1，2)，(1，3)(1，3)(1，3)，(2，3)(2，3)(2，3)。 一队将在第一天到达，在第二天离开。它将停留两天。 第二小组将停留三天。 第三队将停留两天。 求一个安排表，以减少他们停留的总天数。 样例 输入 2 3 4 输出
牛客多校第十场 Tournament（构造）
tomjobs的博客
08-12 562
链接：https://ac.nowcoder.com/acm/contest/5675/I 来源：牛客网 题目描述 You are scheduling a tournament. There are n teams. There are \frac{n(n-1)}{2} 2 n(n−1) ​ competitions against every pair of teams. You can schedule a competition each day. For each team, it will a
2020牛客暑期多校训练营（第十场）—— Tournament
cxkdad的博客
08-10 360
2020牛客暑期多校训练营（第十场）—— Tournament 输入 2 3 4 输出 1 2 1 3 2 3 1 2 1 3 1 4 2 3 2 4 3 4 题目大意 题解 首先，我们看到样例，会想到这个暴力代码： #include<bits/stdc++.h> using namespace std; int main() { int T,n; scanf("%d",&T); while(T--) { scanf("%d",&n);
2020牛客暑期多校训练营（第五场）B、D、E、F、I题解及补题
hzerotole的博客
11-12 616
文章目录2020牛客暑期多校训练营（第五场）题解及补题比赛过程题解A题意解法代码B题意解法代码C题意解法代码D题意解法代码E题意解法代码F题意解法代码G题意解法代码H题意解法代码I题意解法代码J题意解法代码K题意解法代码 2020牛客暑期多校训练营（第五场）题解及补题 比赛过程 这场打出了排名新低，总结原因是前期还行中规中矩，后期两个中等难度的签到题罚时炸了。D和E犯了很多低级的错误，其中E不够熟悉大数板子，而且一开始过于急躁随便就觉得是把所有长度乘起来wa了之后才去认真思考，以后可以多花时间验证思想正确性
2020牛客暑期多校训练营（第七场）A、B、C、D、H、J题解及补题
hzerotole的博客
11-12 607
文章目录2020牛客暑期多校训练营（第七场）题解及补题比赛过程题解A题意解法代码B题意解法代码C题意解法代码D题意解法代码E题意解法代码F题意解法代码G题意解法代码H题意解法代码I题意解法代码J题意解法代码 2020牛客暑期多校训练营（第七场）题解及补题 比赛过程 这场打出了牛客排名新低，原因一来这场题目难度差别较大，我们前期思考的有点慢也wa了很多发罚时炸了，二来读题能力确实不太行，J题读了一小时多才读懂，已经没是没时间写了。 题解 A 题意 给一个半径为rrr的圆，在圆内找到nnn个整数点，求∑i=1n
牛客（多校10）I：Tournament
Mr顺
08-11 273
题目链接 题目意： 你在安排一场比赛。有n支队伍。确实有n(n-1)/2对每一队的比赛。你可以安排每天的比赛。对于每一支球队，他们将在第一次比赛举行的那天到达，在最后一场比赛结束后离开。 例如，有3个团队，时间表是(1，2)，(1，3)，(2，3)。第一队将在第一天到达，第二天离开。它将停留两天。第二队将停留三天。第三队将停留两天。 你想要找到一个时间表，最小化他们停留的天数之和。 示例1： 输入 2 3 4 输出 1 2 1 3 2 3 1 2 1 3 1 4 2 3 2 4 3 4 代码： #in
牛客多校第十场 I-Tournament(思维、构造）
zjllll123的博客
08-12 420
目录题意解题思路代码 题意 链接：Tournament 给出一个数n，请你安排n个队相互之间互打共n(n-1)/2场比赛，一天一场，每个队在需参加的最早的那场进场需参加的最晚的那场退场，问怎么安排才能使他们待的总时间最少 解题思路 由于每个队在需参加的最早的那场进场需参加的最晚的那场退场，而又要使他们待的总时间最少，所以要使大家的等待时间均匀分配，所以就要分成三个部分 前半部分互打 前半部分与后半部分对打 需要注意使后半部分进场均匀，前半部分退场均匀 后半部分互打 有点难理解，以n=10为例，
E. Tournament
多一些不为什么的坚持
12-02 390
题目：E. Tournament 总结：这题用的是贪心。首先对于-1的前部分，一定是不需要考虑的。只需要考虑-1的后部分。接下来每一次的选择对象一定不是前2^k-1,那么可以选择的范围就是2 ^ k~n. 因为第一轮的时候一定是不可能选择第一个的，并且第二或者第三有一个也一定被去掉了，到第二轮的时候前3个此时一定选不到。然后从2 ^ k ~n,选择最小的加其来。用的贪心。 #include &l...
2020暑期牛客多校训练营第十场（I）Tournament（构造）
s260127ljy的博客
08-10 935
Tournament 原题请看这里 题目描述： 您正在安排比赛。 有n个团队。 每对球队都有n(n−1)2\frac {n(n-1)} {2}2n(n−1)​个比赛。 您可以每天安排比赛。 对于每支球队，它将在第一场比赛举行的当天到达，并在最后一场比赛结束后离开。 例如，有3个团队，日程表是(1,2)，(1,3)，(2,3)(1,2)，(1,3)，(2,3)(1,2)，(1,3)，(2,3)。 一队将在第一天到达，在第二天离开。它将停留两天。 第二小组将停留三天。 第三队将停留两天。 您想找到一个时间表，以
2020牛客暑期多校训练营（第十场）I.Tournament(构造/贪心)
小衣同学的博客
11-26 537
2020牛客暑期多校训练营（第十场）I.Tournament(构造/贪心/调整法) t(1
Gym - 101981B - Tournament 2018icpc南京站现场赛B题
c3po
12-06 1430
原文链接  题意 一条直线上有N个村庄，要在这条直线上选K个地方建雕像，使得每个村庄到离其最近的雕像的距离的和最小。输出最小的和。 题解 #include&lt;stdio.h&gt; #include&lt;iostream&gt; #include&lt;algorithm&gt; #include&lt;cmath&gt; #include&lt;cstring&gt; #in...
UPC-5622 Tournament(树的最小深度构造)
kuronekonano的博客
04-24 223
题目描述 N contestants participated in a competition. The total of N−1 matches were played in a knockout tournament. For some reasons, the tournament may not be “fair” for all the contestants. That is, t...
2020牛客暑期多校训练营Drop Voicing(思维，LIS)
ZCETHAN 的博客
07-25 1559
Drop Voicing 题目描述 输入描述: 输出描述: 示例1 输入 6 2 4 5 1 3 6 输出 2 说明 示例2 输入 8 8 4 7 3 6 2 5 1 输出 5 题目大意 给定两个操作： op1:Drop op1:\qquad Drop\,op1:Drop把倒数第二个放到最前面。 op2:Invert op2:\qquad Invert\,op2:Invert把最后一个放到最前面。 现给定一个序列，问最少多少次DropDropDrop操作后会使这个序列变成有序，期间可以任意使用Inv
2020牛客暑期多校训练营Just Shuffle(置换群，逆元)
ZCETHAN 的博客
07-15 1180
题目描述 Given a permutation with size {n}n and an integer {k}k, you should find a permutation substitution {P}P that {1, 2,⋯, n}{1,2,⋯,n} will become {A}A after performing substitution {P}P for exactly {k}k times. Print the permutation after performing {P}P f
2020牛客暑期多校训练营Cover the Tree(构造，dfs序)
ZCETHAN 的博客
07-14 1158
题目描述 Given an unrooted tree, you should choose the minimum number of chains that all edges in the tree are covered by at least one chain. Print the minimum number and one solution. If there are multiple solutions, print any of them. 输入描述: The first line co
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值