2020牛客暑期多校训练营Topo Counting(拓扑排序，组合数学，动态规划)

本文链接：https://blog.youkuaiyun.com/zhangchizc/article/details/107746929

本文介绍了DRG(n)图的拓扑排序问题，通过实例解析了图的构造，并探讨了如何利用动态规划解决该问题。讨论了在不同删除条件下，如何压缩状态并进行转移，最后给出了两种不同的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Topo Counting

题目描述

在这里插入图片描述

输入描述:

在这里插入图片描述

输出描述:

在这里插入图片描述

示例1

输入

2 1073741789

输出

示例2

输入

3 1073741789

输出

7954100

题目大意

给定一个有向图，其形状由 $n$ 单独决定。现在要求这个有向图的拓扑序有多少个。
这个图的建造：
1、有多个子图组成。
2、每个子图里有 $2 * n$ 个节点，其中 $i$ 节点小于等于 $n$ ，则 $i$ 向 $n + i$ 连边。对于一个 $i$ 不等于 $n$ 或者 $2 n$ ，则向 $i + 1$ 连边。
3、各个子图，对于第 $i$ 个子图， $1$ 号子图的 $i - 1 + n$ 号点连向这个子图的 $1$ 号点， $1$ 号子图的 $i$ 号点连向这个子图的 $n + 1$ 号点。

分析

首先要把图给画出来。我们以 $n = 4$ 为例。(随手爬了 $P P T$ 里的图[doge])
在这里插入图片描述
所有的子图实际上最终是连向 $1$ 号子图的，所以就像是 $1$ 号子图是架子， $i (i > 1)$ 号子图是挂在架子上的肉，十分形象地命名为晒肉架图(DRG(n))，其中 $n$ 唯一确定了图。

那么看到这个图，我们发现如果没有图与图之间的连边，我们可以直接分开考虑。用 $d p$ 直接算出每个“肉”的可能然后汇总即可。但是图中是连着的，所以我们为了方便，尽可能地希望它们能够分开，所以就可以分成几种情况考虑。

如果是分开的几个子图，那么如果两个子图的节点数为 $s 1, s 2$ ，拓扑序可能为 $a, b$ 。则两个子图合起来就是 $C_{s1+s2}^{s1}ab$ 。因此如果可以分开就能很好地解决了。

首先，考虑对于一个子图，拓扑时上面这排删掉的点肯定是比下面的多的。而且对于大于一的每个子图，它拓扑的限制就是第一个图与子图的第一条连边。所以只要这条边没有删掉，那么下面这块“肉”是吃不了的。所以可以用一个 $d p$ 维护一下当前我第二排的架子删到了第几个。同样的也要维护第一排的。然后对于每种状态都要维护“肉”有没有被吃，吃了多少。于是，我们列出了一个三维的 $d p [i] [j] [k]$ 。
于是会 $\mathbb{TLE}$ 。

然后分析这个 $d p$ 中存的，发现很多状态是没有用的，比如如果我当前的连边没有删掉，那么对应的“肉”肯定是没有被吃的，所以可以进行压缩。

以下为题解---------------------------------------------------------------------------------------------------------------
如果在完整的图中只删去了一个点的情况，那么我们将其压入状态，只需要一维。设为 $h [n]$ 。
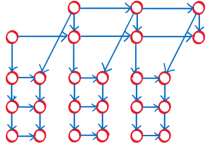
在这里插入图片描述

如果在架子上只删去第一行的2个以上节点，那么需要长度，多一维。此时，该形态唯一地由第一行i和第二行j决定，设为 $f [i, j]$ 。
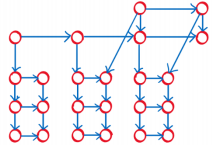
在这里插入图片描述

如果第二行也删了，那么需要一个存肉被吃的程度，也只要两维。此时，该状态由第一行删去的个数i和当前的肉片被咬的程度，即左半面的删去的节点个数j。设为 $g [i, j]$
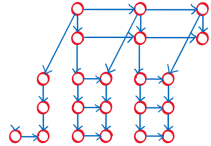
在这里插入图片描述

所以一个 $d p [i] [j]$ 成功压缩。
那么这里解释一下怎么转移：

$Situation1\,\,$ h[n]可以删去第一行的点变成f[n-2,n]或者删去第一片肉的第一个点变成g[n-1,n]。
$Situation2\,\,$ f[i,j]可以继续删第一行的变成f[i-1,j]或者开始删第二行的一个，此时一定会分离出一个完整的肉片，所以可以转移到f[i,j-1]或者是h[j-1]加上一个肉片单独的答案，用之前讲的卡特兰数就可以。
$Situation3\,\,$ g[i,j]同样的可以继续吃肉或者是删第一排的架子，后者会产生一个肉片，因此会转移到g[i,j-1]或者是h[i]和一个肉片的答案。

这就是官方的思路，据此可以得出代码：

代码1

#include<bits/stdc++.h>
using namespace std;
const int N=3010,M=18000010;
long long a[M],b[M];
int f[N][N],g[N][N],w[N][N],ans[N],n,m,mod;
int get(int x,int y){return a[x]*b[y]%mod*b[x-y]%mod;}
int main()
{
    int x,y;scanf("%d%d",&n,&mod);
    m=n*n*2,a[0]=a[1]=b[0]=b[1]=ans[0]=1;
    for(int i=2;i<=m;i++) a[i]=a[i-1]*i%mod,b[i]=mod-(mod/i)*b[mod%i]%mod;
    for(int i=1;i<=m;i++) b[i]=b[i-1]*b[i]%mod;
    for(int i=0;i<=n;i++)
        for(int j=i;j<=n;j++){
            if(i==0) w[i][j]=1;
            else{w[i][j]=w[i-1][j];
                if(i<j) w[i][j]+=w[i][j-1];
                if(w[i][j]>=mod) w[i][j]-=mod;
            }
        }
    for(int j=2;j<=n;j++){
        if(j>=3) y=f[0][j-1]; else y=ans[0];
        x=(j-1)*(n*2+1)-n*2;
        (f[0][j]+=1ll*w[n][n]*y%mod*get(x+n*2,n*2)%mod)%=mod;
    }
    for(int i=1;i<n;i++){
        for(int j=0;j<=n;j++){
            x=2*i-1+(i-1)*(n*2);
            g[i][j]=1ll*w[j][n]*ans[i-1]%mod*get(n+j+x,x)%mod;
            if(j!=0) (g[i][j]+=g[i][j-1])%=mod;
        }
        ans[i]=f[i-1][i+1]+g[i][n];
        if(ans[i]>=mod) ans[i]-=mod;
        for(int j=2;j<=n;j++){
            f[i][j]=f[i-1][j];
            if(j-1>i+1) y=f[i][j-1];
            else y=ans[i];
            x=i+(j-1)*(n*2+1)-n*2;
            (f[i][j]+=1ll*w[n][n]*y%mod*get(x+n*2,n*2)%mod)%=mod;
        }
    }
    printf("%d\n",ans[n-1]);
    return 0;
}

但是神仙队友DNdalao写了如下的代码，显然，三个数组是可以压缩的。~~具体的就请各位细品了，在下也不是很理解，怕菜鸡带偏各位（滑稽）。~~

代码2

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN=2e7+10;
ll n,MOD,inv[MAXN],jc[MAXN],dp[3010][3010];
ll ksm(ll a,ll p)
{
    ll ret=1;
    while(p){
        if(p&1) ret=ret*a%MOD;
        a=a*a%MOD;p>>=1;
    }return ret;
}//快 速 幂
ll C(ll n,ll m)
{return jc[n]%MOD*inv[m]%MOD*inv[n-m]%MOD;}
ll CTLS(ll n,ll m)
{return (C(n*2-m,n)-C(n*2-m,n-m-1)+MOD)%MOD;}
//卡 特 兰 数
int main()
{
    scanf("%d%d",&n,&MOD);
    jc[0]=dp[0][0]=1;
    for(int i=1;i<MAXN;i++) jc[i]=jc[i-1]*i%MOD;
    inv[MAXN-1]=ksm(jc[MAXN-1],MOD-2);
    for(int i=MAXN-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%MOD;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++){
            if(i==n-1&&j==n-1) continue;
            int l=2*n*n-min(i,j)*n*2-i-j-2;
            if(j==i+1){
                for(int k=0;k<=n;k++)
                    dp[i+1][j]=(dp[i+1][j]+dp[i][j]*C(l-k,n*2-k)%MOD*CTLS(n,k)%MOD)%MOD;
            }//如果只删去一个
            else{
                dp[i+1][j]=(dp[i+1][j]+dp[i][j])%MOD;
                if(i==j) dp[i][j+1]=(dp[i][j+1]+dp[i][j])%MOD;//删掉了肉
                else dp[i][j+1]=(dp[i][j+1]+dp[i][j]*C(l,n*2)%MOD*CTLS(n,0)%MOD)%MOD;//没有删肉
            }
        }
    printf("%lld\n",dp[n-1][n-1]);
}

END

DNdalaoNB！！！%%%