2020牛客暑期多校训练营Bogo Sort(置换群，分解质因数，大数乘法)

Bogo Sort

题目描述

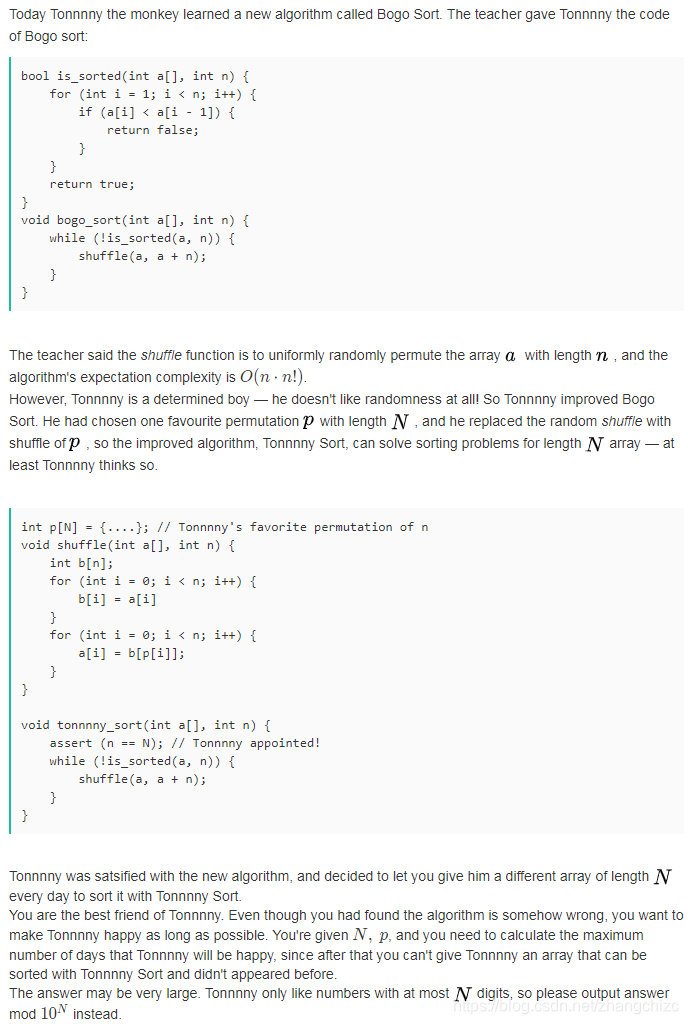
输入描述:

输出描述:

示例1

输入

5
1 2 3 4 5

输出

1

示例2

输入

6
2 3 4 5 6 1

输出

6

题目大意

给定一串数列$p[]$，有变换：
$for(inti=0;i<n;i++)$
$b[i]=a[i]$
$for(inti=0;i<n;i++)$
$a[i]=b[p[i]]$
求$1\sim n$的序列的所有排列中，有多少序列可以通过$p$的上述变换而变成$1\sim n$的有序数列。

分析

置换群

分析这个变换的过程，所有的$a[i]$都变成了$a[p[i]]$，很容易可以看出这就是一个置换群的变换。我在第二场的J题里放了其概念，看官也可以上网自行搜索。（真就牛客多校的特色是置换了）

所以这就是要找到$1\sim n$的原数列经过多少次变换后会变回原数列。

如果有$p:3,1,2,5,4$，那么前三个每3次变换就能回到原位，而后两个每2次变换就能回到原位。那么显然总的是需要$lcm(2,3)=6$次变换使得它们都回到原位。

因此，对于这题，我们只需要求出每个群的大小，然后求一下$lcm$即可。题目有点沙雕的是说要$mod10^N$，但是显然，这是不会达到的，所以不需要$mod$。但是问题是这些$lcm$算出来可能爆$longlong$，所以需要用到高精度。

高精度

问题是高精度求$lcm$是个麻烦的事情，万幸的是，这些群的大小都是$int$型的，因此$gcd$是很好求的。可是要用到大数除，诶这就有点麻烦了，对于一个根本忘了怎么写高精度的蒟蒻来说，除法是个难于上青天的事情。

但是蒟蒻脑子好使，可以用另一种方式来求$lcm$。考虑分解质因数，对于每个质数记录每个数的质因数的个数的最大值，有点绕呵，举个例子吧。
比如有$2,3,4$要求它们的最小公倍数，则我只要分解：
$2=2$
$3=3$
$4=2\ast 2$
那么$2$有$max(1,2)$次，3有$1$次，因此它们的最小公倍数是$2^2\ast 3^1=12$，没有问题。它的原理是：任意一对数，它们如果有质因子相同，那么根据$lcm=a\ast b/gcd$可知，它会将公共的部分除掉，相当于对于每个质因子的个数求个$max$即可。比如有质数$pr$，$a=p{r}^3\ast ...b=p{r}^5\ast ...$，则它们的公共部分是$p{r}^3$，相乘之后有$p{r}^8$，除掉后有$p{r}^5$也就是$p{r}^{max(3,5)}$。

所以只要对于每个质数都求在不同数里的$max$，然后相乘就是$lcm$，避免了除法。只要用到高精乘低精就可以AC。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll MAXN=1e5+100;
int pr[MAXN],pp[MAXN];//质数专用
bool vis[MAXN];//判断每个数是否已经被算进群了
int a[MAXN],len=1,ans[MAXN],n,sz[MAXN],tot=0,cnt=0;//ans  高精度用  sz  群的大小
void mul(int x){
    for(int i=1;i<=len;i++) ans[i]*=x;
    for(int i=1;i<len;i++)if(ans[i]>9) ans[i+1]+=ans[i]/10,ans[i]%=10;
    while(len<n&&ans[len]>9) ans[len+1]+=ans[len]/10,ans[len++]%=10;//这里的len<n是因为一开始的位数限制，但是后来发现不用
    ans[len+1]=0;
}//高精乘低精
int main()
{
    for(int i=2;i<MAXN;i++) if(!pr[i]){for(int j=i*2;j<MAXN;j+=i) pr[j]=1;pp[++cnt]=i;}//筛质数，注意j+=i，一开始手抖，WA了一遍QAQ
    ans[1]=1;//一开始=1，那么乘上去会有效
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        if(!vis[i]){
            vis[i]=1;//标记已经访问
            sz[++tot]=1;
            for(int j=a[i];j!=i;j=a[j])
                vis[j]=1,sz[tot]++;//用a[i]去遍历群，然后记录大小
        }
    memset(pr,0,sizeof(pr));//这里换了作用，是记录每个素数的max
    for(int i=1;i<=tot;i++)
        for(int j=1,t=0;j<=cnt&&sz[i]>1;j++){
            while(sz[i]%pp[j]==0) t++,sz[i]/=pp[j];//把每个数的质因子的个数求出来
            pr[pp[j]]=max(pr[pp[j]],t);t=0;//求最大值
        }
    for(int i=1;i<=cnt;i++) while(pr[pp[i]]--) mul(pp[i]);//把每个质数都乘上去就可以算lcm了
    for(int i=len;i>=1;i--) printf("%d",ans[i]);//逆向输出哦
}

END

难得，自己WA了好几遍居然在比赛的时候AC了。