2020牛客暑期多校训练营Ancient Distance(二分+贪心+dfs序+线段树)

Ancient Distance

题目描述

输入描述:

输出描述:

示例1

输入

3
1 2
3
1 1

输出

3
2

说明

备注:

题目大意

……备注里的话有点……。给定一棵树，树上有一些关键点$(key)$。要求对于 k ∈ { 1 , 2 , . . . , n } k \in\{1,2,...,n\} k∈{ 1,2,...,n}个关键点，求所有节点的$AncientDistance$的最大值最小是多少。其中，$AncientDistance$是这个节点在到根节点$root$的路径上第一个$key$的距离。
备注：如果你有了结果，勇敢地尝试吧

分析

看到题目中说，求最大值的最小，第一个想法就是二分答案。虽然$dalao$用分块，但是蒟蒻还是用二分。二分$k$个节点的最大值，然后验证答案即可。

那么问题来了，怎么验证答案呢？？？
一下我们分几个问题进行分析：

dfs序

首先，我们对这棵树进行dfs序的标号（不计回溯）：

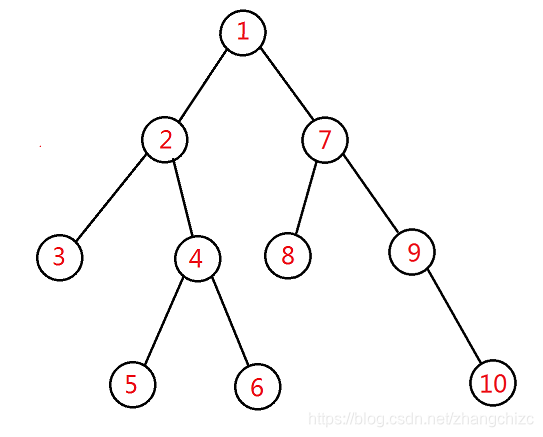
对此，可以跑一次$dfs$，记下$dfn$。然后，我们发现可以对这棵树进行操作——展开变成线段。

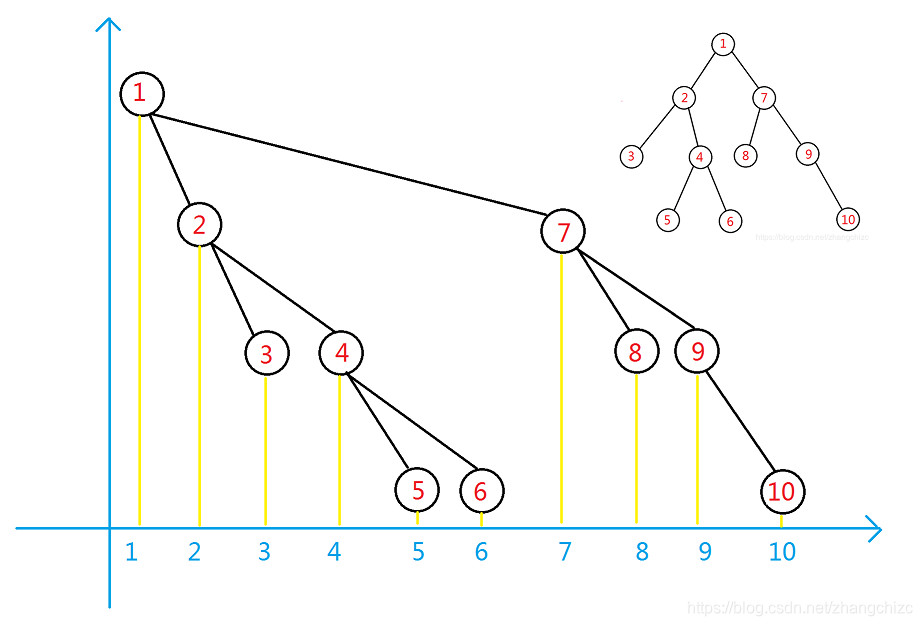
此时，如果我们需要对$2$的子树操作，就是对区间$2...6$进行操作。

线段树

此时，已经展开的树就可以用线段树进行修改和查询了。

但是开头的问题是，怎么验证？我们可以考虑求出每个节点的深度，然后从最深的节点开始，向上$k$层，就能使得$AncientDistance$最大为$k$。此时，我们将向上$k$层的节点设为$key$，则整棵子树都有了$AncientDistance$，以上图 k = 2 k=2