目录
介绍堆排序
上次讲解了冒泡排序,冒泡排序是一种稳定的排序方式,这次介绍一种不稳定的排序方式:堆排序,他会提供另一种思路进行排序.
二叉树简介
想要学习堆排序,首先,需要学习二叉树的概念,并直到完全二叉树的概念,在了解二叉树之前,首先向大家介绍树的概念,树是由一个根节点和若干个子节点组成的

树的根节点
为了便于理解,用现实中的树来介绍,如上图:树的根就类似树的根节点.
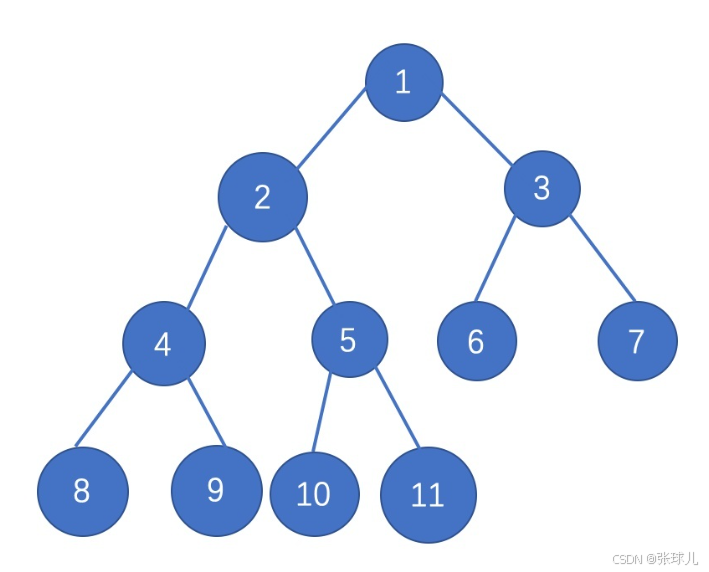
下图中的数字1则是根节点
根节点的特点和树也有相似之处:
1.根节点只能有一个,同一般一棵树只有一个树根
2.根节点没有父节点
除此之外,根节点还有很多作用,可以把左右数据分割,最大(小)值等...
树的父节点
在树结构中,对于除根节点以外的任意节点,其父节点是指在树的层次结构中,直接连接到该节点并且更靠近根节点的节点。如上图,2是4和5的父节点,且只能上一级的称为父节点,上两级则不是.
树的子节点
子节点是相对于父节点而言的。在上图树的结构中,8和9是4的子节点,与父节点相对,相信也很好理解.
树的叶子结点
没有子节点的节点称之为叶子结点,向上面的8,9,10,11节点则称之为叶子结点.
二叉树概念介绍
上面介绍几个节点也是为了介绍二叉树做铺垫,二叉树是一种树形结构,他的任何节点的子节点个数不大于2,因此叫做二叉树,相信由上面的概念介绍后,理解起来很简单了.
堆排序
堆排序则是基于二叉树来排序的,首先需要进行向下调整
向下调整
向下调整操作是堆排序中的关键步骤之一。其基本思路是针对一个满足堆性质(比如大顶堆要求父节点的值大于等于子节点的值,小顶堆要求父节点的值小于等于子节点的值)的完全二叉树,当某个节点(通常是根节点)的值发生改变,导致堆的性质可能被破坏时,需要从该节点开始向下调整,使得调整后的子树依然满足堆的性质。
以大顶堆为例,假设当前要对节点 i 进行向下调整(这里节点编号从 0 开始,节点 i 的左子节点为 2i + 1,右子节点为 2i + 2),操作过程如下:
首先,比较节点 i 的左、右子节点(如果存在的话),找到其中值较大的那个子节点,记为 max_index。然后将节点 i 的值与 max_index 所对应节点的值进行比较,如果节点 i 的值小于 max_index 对应节点的值,那就交换这两个节点的值,接着再以 max_index 对应的节点为新的起点,继续向下进行上述比较和调整操作,直到该节点的子节点都小于它或者到达了叶子结点,此时就完成了一次向下调整,保证了以该节点为根的子树满足大顶堆的性质。
构建初始堆
在进行堆排序前,要先将待排序的数组构建成一个初始堆(比如大顶堆或者小顶堆)。对于给定的无序数组,从最后一个非叶子结点开始(对于长度为 n 的数组,最后一个非叶子结点的索引为 n/2 - 1 向下取整),依次对这些非叶子结点执行向下调整操作,经过这样一轮的操作后,整个数组对应的完全二叉树就构成了一个满足堆性质的堆结构。
堆排序的过程
- 构建初始堆:如前面所述,根据待排序数组构建出初始堆(假设构建大顶堆),此时堆顶元素就是数组中的最大元素。
- 交换堆顶和数组末尾元素:将堆顶元素(也就是当前最大元素)与数组的最后一个元素进行交换,这样最大元素就被放到了数组的正确排序位置(即数组末尾),而原数组末尾元素被换到了堆顶位置。
- 调整堆:对交换后的堆顶元素进行向下调整操作,使其再次满足大顶堆的性质,此时堆顶元素又变成了剩余未排序元素中的最大元素。
- 重复步骤 2 和 3:不断重复交换堆顶和当前未排序部分的末尾元素,以及调整堆的操作,直到整个数组都完成排序,也就是所有元素都被放置到了正确的位置上。
堆排序的代码
def sift(li, low, high):
i = low # 因为是堆顶,之后堆顶要换位置,要提前赋值
j = 2 * i + 1
tmp = li[low] # 可以写li[i]
while j <= high: # 判断在不在堆中
if j + 1 <= high and li[j + 1] > li[j]: # 先判断是否超出list
j = j + 1
if tmp < li[j]:
li[i] = li[j] # 把儿子结点的最大值赋值给堆顶
i = j # 往下一级
j = 2 * i + 1 # 堆顶的儿子改变
else:
li[i] = tmp # 当上领导了,比下面的都大
break
else:
li[i] = tmp # 底下没人了,叶子上面位堆排序向下调整的过程的代码,下面将展示堆排序的整个过程:
def heap_sort(li):
n = len(li)
# 从最后一个叶子结点的父节点开始向下调整
for i in range((n - 2) // 2, -1, -1):
sift(li, i, n - 1)
# 把数从根节点拿出来排序,从n-1开始,排好一个,往前一位
for i in range(n - 1, -1, -1):
li[i], li[0] = li[0], li[i]
sift(li, 0, i - 1)堆排序的时间复杂度
堆排序的时间复杂度在平均情况、最好情况和最坏情况下都是 O (nlogn),这使得它在处理大规模数据排序时效率相对较高。
堆排序的空间复杂度
堆排序是一种原地排序算法,它只需要常数级别的额外空间来辅助完成排序过程,其空间复杂度为 O (1)。
堆排序的稳定性
堆排序是一种不稳定的排序算法,例如在排序过程中,相同元素的相对顺序可能会发生改变。比如对于数组 [5, 5, 3] 进行堆排序,可能出现原本在前的 5 在排序后跑到了后面的情况,导致相同元素的先后顺序发生了变化。
适用场景
堆排序由于其时间复杂度相对稳定且不需要大量额外空间,比较适合对数据量较大且对空间要求较为严格的情况进行排序,例如在一些内存有限但需要高效处理大量数据排序任务的系统中,堆排序就能发挥较好的作用。






















 4593
4593

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








