矩阵幂法求Fibonacci数 复杂度O(logn)

求Fibonacci数，用递归法复杂度O(2 ^ n)，用动态规划法能优化到O(n)，参考：

动态规划算法入门——Fibonacci数列、过桥问题

其实还有更快的做法：矩阵幂法。

设{Fn}是Fibonacci数列，则有：

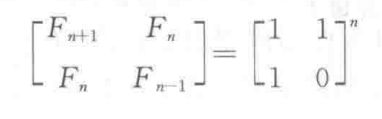
可用归纳法证明：当n=1时，F(2) = F(1) = 1, F(0) = 0，满足上式；当n>1时，四个元素分别为F(n+2) = F(n+1) + F(n), F(n+1) = F(n+1), F(n+1) = F(n) + F(n-1), F(n) = F(n)。

所以计算F(n)转换成了计算矩阵的n-1次幂。

两个二阶矩阵相乘，需要做8次乘法，是个常数，那么算法复杂度只取决于矩阵之间相乘的次数。

考虑计算a ^ n，若暴力求解需要n - 1次乘法；若考虑分治法，则有：

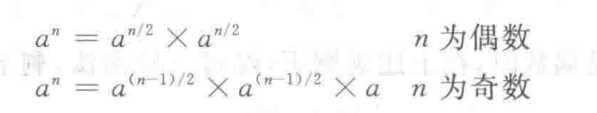
(注意奇偶需要分别考虑)

最坏时间复杂度:
W(n) = W(n/2) + O(1)
W(1) = 0

所以 W(n) = O(logn)

求Fibonacci数的复杂度便也降低到了O(logn)次。