Peter算法小课堂—DP的应用

最新推荐文章于 2024-04-12 18:59:43 发布

原创最新推荐文章于 2024-04-12 18:59:43 发布 · 249 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

动态规划专栏收录该内容

11 篇文章

订阅专栏

本文介绍了动态规划在编程中的应用，包括基本概念、线性DP问题实例（如魔鬼的步伐问题）以及求解最大连续子序列和和最长下降子序列的方法。通过实例演示了状态转移方程的运用和代码实现。

大家好，我是Peter，我又来啦🎈🎄✨

🎈🧨🎉《动态规划》专栏来啦，目前为止，此专栏已经有三篇文章啦🎁🎀🎄

1.DP概念与编程方法 DP概念和编程方法-优快云博客

2.Peter算法小课堂—经典线性DP问题（上）Peter算法小课堂—经典线性DP问题(上）-优快云博客

3.Peter算法小课堂—经典线性DP问题（下）Peter算法小课堂—经典线性DP问题（下）-优快云博客

魔鬼的步伐（太戈编程第452题）

太戈编程网站：太戈编程 (etiger.vip)

452. 魔鬼的步伐2（Best AC by 陈全）

题目描述

魔鬼共有n级楼梯要走，魔鬼有他的步伐，每一步他只可以向上走a级楼梯或者b级楼梯，请问走到第n级台阶至少要几步？走不到时输出-1。

算法思路

我们令f[i]为“每一步向上走a级楼梯或者b级楼梯，走到第i级台阶至少要几步”。我们现在再思考状态转移方程，分类讨论。

第一种情况，i>=a。我们有分两种情况，①走a级楼梯：那么我们必须保证第i-a级台阶得走到，所以此时f[i]=f[i-a]+1。②不走a级楼梯：那么我们f[i]主要看b级楼梯走不走，所以暂时f[i]=f[i]。然后，我们取最小值，也就是f[i]=min(f[i],f[i-a]+1)

第二种情况，i>=b。我们模仿第一种情况的状态转移方程，得到f[i]=min(f[i],f[i-b]+1)。

这时，我们突然看到题目上写着一行字，叫“走不到时输出-1”，这个东西😰看起来很麻烦！其实很简单，我们在for循环里写这么一句话“f[i]=INF”，最后输出时写if(f[n]==INF) cout<<-1;其实就解决啦！😎😁

给出代码吧

#include <bits/stdc++.h>
using namespace std;
const int N=1009;
const int INF=1e9;
int n,a,b,f[N];
int main(){
    freopen("steps.in","r",stdin);
    freopen("steps.out","w",stdout);
	cin>>n>>a>>b;
	f[0]=0;
	for(int i=1;i<=n;i++){
		f[i]=INF;
		if(i>=a) f[i]=min(f[i],f[i-a]+1);
		if(i>=b) f[i]=min(f[i],f[i-b]+1);
	}
	if(f[n]==INF) cout<<-1;
	else cout<<f[n];
	return 0;
}

最大连续子序列和

题目的话大家看字面意思就懂了哈，我们主要思考状态转移方程。

状态定义

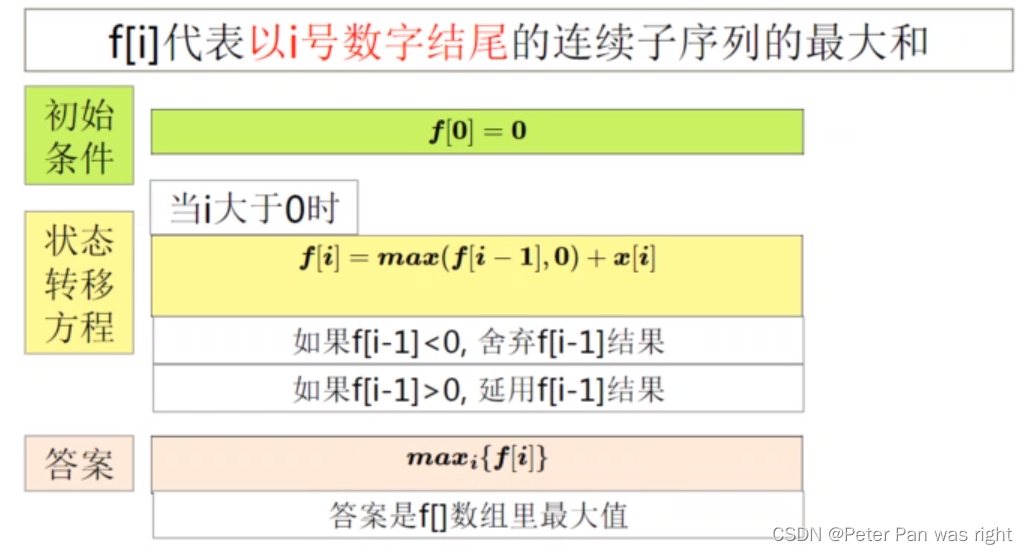
我们考虑两种状态定义：A：前i个数字里最大连续子序列和 B：以i号数字结尾的连续子序列的最大和，显然我们选择B，因为A压根找不到状态转移方程啊。

状态转移方程

我们在计算f[i]时，我们可以选择延用f[i-1]，或者不延用。所以说状态转移方程如下图所示

最后来个代码

cin>>n;
for(int i=1;i<=n;i++) cin>>x[i];
f[0]=0;
for(int i=1;i<=n;++i){
	f[i]=max(f[i-1],0);
}
int ans=*max_element(f+1,f+1+n);
cout<<ans<<endl;

最长下降子序列

cin>>n;
for(int i=1;i<=n;i++) cin>>x[i];
f[0]=0;
for(int i=1;i<=n;i++){
	f[i]=1;
	for(int j=1;j<i;j++){
		if(x[j]>x[i]) f[i]=max(f[i],f[j]+1);
	}
}
int ans=*max_element(f+1,f+1+n);
cout<<ans<<endl;

🎈🎄✨希望大家能有所收获，有问题的话可以评论。🎈🎄✨