预测医疗器械可浸出物暴露

预测患者接触医疗器械浸出物的进展

短标题：预测可浸出物暴露

摘要

医疗器械材料含有化学物质，如果释放量足够大，可能会引发毒理学担忧。目前越来越多地采用毒理学风险评估方法来替代动物实验以解决这些担忧。当前，这些方法主要依赖in vitro提取测试来估计患者暴露于可能从器械材料中浸出的化学物质的风险，但测试结果的临床相关性往往不明确。最近的研究进展表明，基于物理的模型可用于提供更具临床相关性的暴露估计。然而，可用于参数化和验证这些模型的数据缺乏，阻碍了其常规应用。本文概述了这些方法，包括开发和参数化暴露模型时的考虑因素、应对数据有限挑战的策略，以及潜在的未来方向和改进措施。

关键词
风险评估；毒理学；扩散；溶解度；聚合物；理论模型；分子动力学仿真

引言

医疗器械是一类多样化的生物医学产品，可由多种材料组成，具有截然不同的预期用途。传统评估医疗器械生物学安全的方法是采用体外和/或体内生物系统进行试验（ISO 10993‐1:2018）。然而，开展包括长期全身毒性及/或遗传毒性在内的全套传统生物学试验成本高昂且耗时。

2016年，美国食品药品监督管理局（FDA）器械与放射健康中心（CDRH）提出将化学和毒理学风险评估作为评估医疗器械安全性时替代传统方法的途径，用于解决遗传毒性、致癌性、全身毒性以及生殖/发育生物学终点等问题（CDRH，2016）。该替代方法利用特定终点的化学毒性信息以及对潜在暴露的假设，判断医疗器械是否含有需要进一步采取风险控制措施的有害物质。在应用化学/毒理学风险评估方法时，必须评估所有可能从医疗器械中析出的有害化学物质。采用替代性预测毒理学方法来评估医疗器械安全是FDA的重点方向（国家科学院，2017；FDA，2019）。

化学毒理学风险评估的一个关键组成部分是估算在医疗器械可能使用的最坏情况条件下，个体可能接触到的可浸出化学物质的最大暴露剂量（ED max）。然而，目前尚无建立ED max的标准方法。取而代之的是，常利用不能代表临床使用情况的非靶向提取研究（即，筛选）并基于保守假设来获得ED max。对于每种被提取的化学物质，将其ED max与可耐受摄入量（TI）值进行比较。对于医疗器械，ISO 10993‐17:2002 提供了一种推导TI的方法，以保护人体免受特定化学物质引起的不良健康效应。通过TI与ED max的比值、化学物质毒性信息以及临床使用信息，对已识别化学物质的毒理学风险进行表征。通常无法获得实际接触医疗器械可浸出物的情况。此外，对于长期植入器械，通过获取所有可浸出物的ED max来确定暴露水平也存在困难。

在不了解医疗器械可能释放哪些化学物质的情况下，通常很难在体外模拟临床条件。对于长期接触人体的医疗器械而言，由于需要在多个时间点获取数据，估算非目标可提取物的每日释放量也可能因耗时和成本高昂而不切实际。由于这些问题，提取研究通常在升高温度和强分析溶剂条件下进行；然而，这可能导致测试结果的临床相关性不明确。

在将体外提取数据用于毒理学风险评估时，风险评估者需对医疗器械在使用中的临床条件下可能释放的情况做出假设。对于长期接触人体的医疗器械，一种常用的方法是假设提取出的总累积量在身体接触的整个持续时间内以恒定速率释放，这类似于职业流行病学中的剂量模型（克里贝尔、切考威和皮尔斯，2007；切考威和赖斯，1992）。换句话说，通过将器械中某种可浸出物的总量除以器械与人体接触的天数，得到每日释放率。理论上，当医疗器械在实际临床条件下使用时，这种方法可能会低估多个数量级的毒理学风险。另一种更为保守的暴露剂量估计方法是假设器械中可浸出化学物质的总量每天均被完全释放（CDRH，2016）。尽管后一种方法通常被认为是具有保护性的，但它可能导致极度保守的暴露估计。因此，目前用于估算患者暴露的方法，在对医疗器械可浸出物进行毒理学风险评估时，并未基于物理、生理或临床决定因素。幸运的是，近年来在应用基于物理的传输模型方面已取得进展，这些模型能够为器械可浸出物提供更具临床相关性且仍然保守的患者暴露估计，这也是本综述的主题。

基于物理的浸出模型

基于物理的浸出模型在多种应用中备受关注，包括食品包装材料暴露的建模（方与维特拉克，2017；贝利等人，2005），尽管通过审慎（且保守）地选择边界条件来消除对组织特异性数据的需求可以显著提高模型的可处理性，但器械材料的复杂性也可能成为建立充分描述仅材料内部化学物质传输关键物理过程模型的重大障碍。器械材料可能由多相组成，并在临床使用过程中发生溶胀和/或降解。

虽然在模型中纳入这些复杂性相对直接，但由此产生的控制方程将包含大量未知参数，这些参数可能依赖于材料内的浓度和相态，需要加以确定（赛勒、福瑞、金和沃伦，2016）。多种实验技术，例如测量吸附动力学（帕西涅米，1995；马马利加、沙贝尔和金德，2004）、样品原位或超薄切片后的浓度分布分析（罗伊、贝尔和吉内夫斯基，1974；赛勒等人，2018），以及放射化学方法（约克什，1987；杜比尼、奇凯蒂、维卡里奥和布亚，1967），可能需要用于在这些参数的可实现范围内量化特定材料体系的这些参数。因此，获取用于参数化和验证模型所需的数据可能会非常困难。

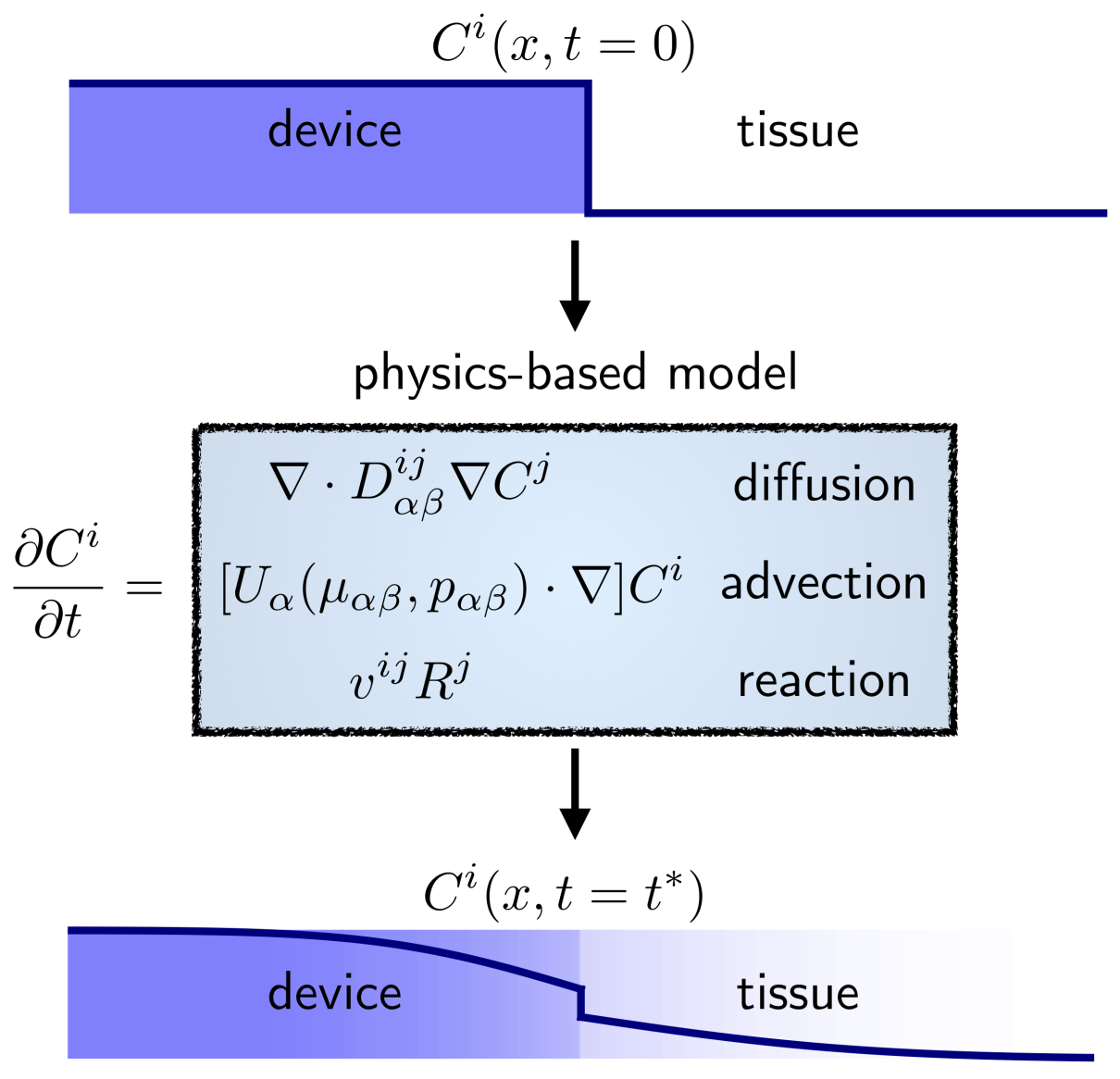
在许多器械场景中，可以采用更简单的模型。例如，如果基质材料是宏观均质的，并且在体内不发生溶胀或降解，且可浸出物仅以稀释浓度存在，则可浸出物在基质内的传输仅可通过标量扩散系数来描述。因此，可以开发仅需了解器件几何结构、可浸出物的初始分布以及单一材料参数的保护性模型。如果可浸出物是主体添加剂或杂质，使其在基质内以初始浓度均匀分布，则模型的复杂性可进一步降低。此外，对于绝大多数医疗器械，其几何结构可保守地表示为具有暴露表面积（A）的半无限介质。这些考虑因素导出了一个关于可浸出物最大质量的模型，该模型描述了随时间从器械释放的可浸出物的最大质量，且仅需了解这三个参数（赛勒等人，2019）：

$$
M(t) \leq 2AC_0 \sqrt{\frac{Dt}{\pi}}
$$

公式1 可在满足基本假设的各种器械场景中，提供一种简单且保守的基于物理原理的浸出速率预测方法。我们注意到A通常是已知的，在有意添加物含量已知的情况下，可能通过a priori知识确定，或通过强化提取测试获得C₀。然而，系统特异性值的获取可能具有挑战性。

扩散系数

建立系统特异性值最直接的方法是基于实验测量。获得聚合物基质中可浸出物数值的常用实验方法是吸附实验，即将纯聚合物与固定量的可浸出物接触，监测其随时间的质量吸收情况，并持续实验直至达到平衡。随后可通过将随时间变化的质量吸收数据拟合到适当的扩散方程解中来估算该值（克兰克，1979）。对于低分子量浸出物（M < 100克/摩尔），重量法蒸气吸附技术非常有效，可连续监测聚合物样品随时间的质量吸收（贾恩斯、钱德拉塞卡尔、伍尔福德和路德维希，2017）。

对于扩散较慢的较大浸出物，传输参数的实验测定可能更具挑战性。例如，聚合物器件组件中存在的添加剂通常在100至1000克/摩尔之间（巴特，2005）。对于这些较大的分子，必须将聚合物暴露于含有溶解浸出物的液相溶液中进行液体吸附实验。例如，液体吸附实验已被用于表征与器械相关的聚合物中的多种着色剂（Chandrasekar等，2018；钱德拉塞卡尔等人，2018a）。虽然监测纯聚合物的整体质量吸收是评估的最直接方法，但其他技术如浓度分布分析（罗伊、贝尔和吉内夫斯基，1974；赛勒等人，2018）、扩散池（莫里西和韦塞利，2000）以及标记技术（约克什，1987）也经常被使用。

然而，根据浸出物尺寸和聚合物特性（例如结晶度百分比和Tg），为特定系统实验建立可能需要相当长的时间。例如，在PEBAX 4033中对一种着色剂——酞菁锰的表征，需要进行为期32周的液体吸附实验（钱德拉塞卡尔等人，2018a）。

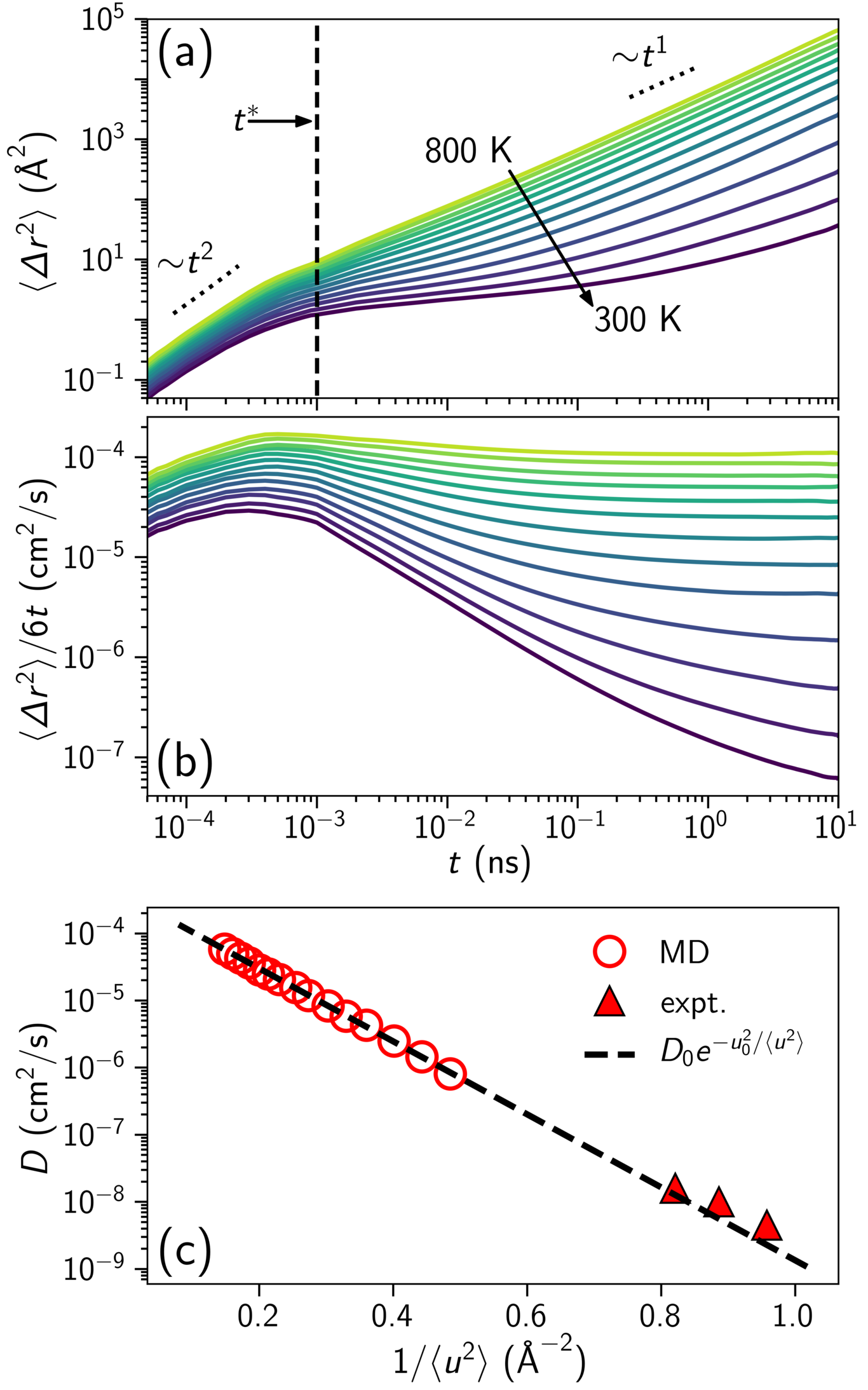
分子动力学（MD）模拟提供了一种量化的方法。分子动力学（MD）模拟可以揭示添加剂分子的原子尺度轨迹，其均方位移与扩散率的关系为：

$$
\langle \Delta r^2 \rangle = 6D \lim_{t \to \infty} \frac{d \langle \Delta r^2(t) \rangle}{dt}
$$

如图2所示。通过分子动力学（MD）获得的值如果已完全收敛，则可以非常精确，实际上这意味着必须足够大（安德森、杨和埃迪格，2018；福雷等人，2014；古塞夫、穆勒‐普拉特、范冈斯特伦和苏特，1994）。与实验方法类似，所需时间取决于浸出物尺寸和其他条件（例如温度、添加剂浓度等）。对于在足够高温度下的低分子量添加剂，模拟时间仅需几纳秒即可收敛，相当于实际时间中的几个小时（安德森、杨和埃迪格，2018；福雷等人，2014；古塞夫、穆勒‐普拉特、范冈斯特伦和苏特，1994）。然而，在生理温度下对于较大的添加剂，这些模拟可能需要长达数月的实际时间（福雷等人，2014；李、基尔德西格和朴，199）。

近年来，随着理论发展将局部短时间溶质动力学与长时间扩散联系起来，出现了一种可能加速该计算的方法（帕兹米诺·贝坦科尔特、哈纳卡塔、斯塔尔和道格拉斯，2015；道格拉斯、帕兹米诺·贝坦科尔特、童和张，2016；赛勒、贾瓦赫里、西尔弗斯坦和福雷，2016）。这些方法利用德拜‐沃勒因子来考察溶质的局域化行为，该因子用于衡量在扩散跳跃事件之间瞬态“笼状”结构的大小。通过短时间的分子动力学模拟可在高温下快速量化和（D ⟨u²⟩）。然后，利用与之间的关系方程，可实现向较低温度的有限外推（图2c）。要进一步扩展这种外推的低温极限，尤其是在Tg附近，仍需进一步的理论发展（道格拉斯、帕兹米诺·贝坦科尔特、童和张，2016）。

其他一些模拟技术也颇具前景，包括动力学蒙特卡洛（内尔茨和布朗，2010）和加速动力学方法（沃特、蒙塔伦蒂和格尔曼，2002），但它们在聚合物中分子扩散的有效性尚未得到充分验证。

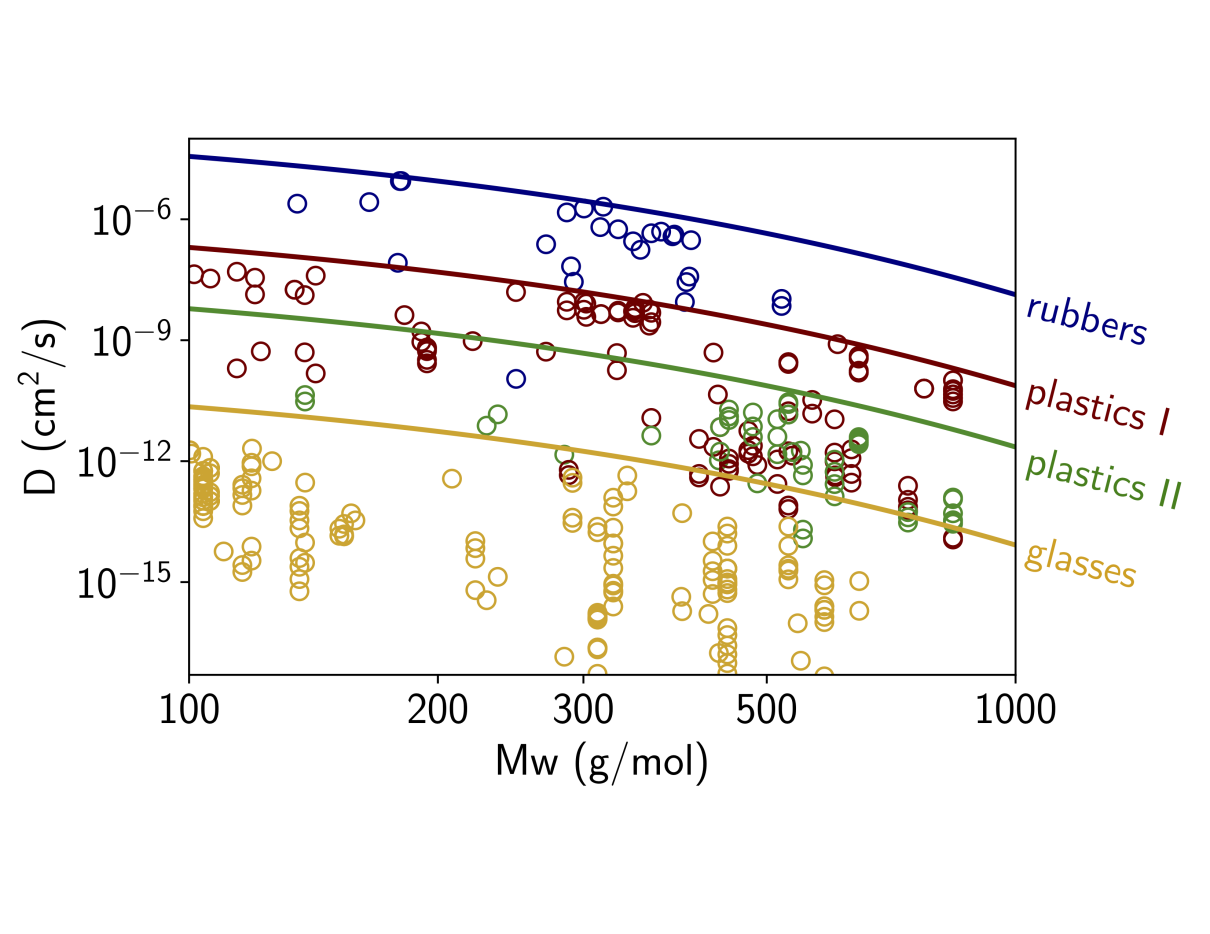
尽管可以通过实验测量或分子动力学模拟来获得系统特异性扩散系数，但这些方法可能需要数月或数年才能完成。因此，目前尚不可行将这些方法常规用于评估。另一种方法是利用文献中已有的测量数据，为特定基质（贝利等人，2005；霍克斯特拉等人，2015）或基质类别（赛勒等人，2019；施沃普、戈丹和里德，1992）建立保守限值。图3展示了该方法的一个示例。在图中，使用了来自文献的汇总数据，基于特定类别内测量数据D(Mw)所体现的最快“皮林格模型”（贝利等人，2005）关系，为四种不同类别的聚合物基质建立保守限值。此外，还提出了更复杂的方法，以从稀疏数据中推导出保守值，从而减少高估程度，同时在预定义的统计概率范围内保持保守性（方与维特拉克，2017）。鉴于测量系统特异性参数存在障碍，目前最简便的方法是基于现有数据建立保守限值，用于参数化基于物理机制的暴露模型，以支持医疗器械可浸出物的毒理学风险评估。

未来机遇

如果系统符合基本假设且已确定D，则公式1应能提供一个保守的暴露量估计值。然而，在许多系统中，这种估计可能会显著高估实际暴露量。例如，如果可浸出物在基质材料中溶解度很低，主要以相分离的颗粒形式存在，则扩散传输速率可能远低于公式1的预测值。在此类情况下，使用希古奇模型（希古奇，1961；保罗，2011）更能准确描述浸出行为，该模型将公式1中的扩散系数替换为有效扩散系数：

$$
D_e = \frac{\pi S^2 C_0}{2} D
$$

其中 $ S $ 是可浸出物在基质中的平衡溶解度。因此，浸出速率与 $ S $ 成正比而减慢。尽管最初是为预测药物递送系统中的药物释放而开发的，但公式2已被证明能准确描述医疗器械聚合物中其他添加剂的浸出行为（钱德拉塞卡尔等人，2018a）。幸运的是，$ S $ 可以通过吸附实验直接获得，前提是将聚合物样品浸入可浸出物的饱和溶液中。或者，也可通过汉森或希尔德布兰德溶解度参数（Barton，1991）、基团贡献法（巴纳，2000；范克雷夫伦和特尼亨伊斯，2009）或定量结构/性质关系（QSPRs）（德拉尼，2005；曼霍尔德，波达奥斯特曼和泰特科，2009）进行估算。

同样，已有多种分子动力学模拟方法可用于预测小分子溶解度，例如热力学积分、自由能微扰和威多姆插入（弗伦克尔和斯密特，2002）。这些理论与计算方法在食品包装（特拉尼和德索布里，2004）和药物递送（梅达雷维奇、朱里斯、巴尔帕莱西斯、卡赫里马尼斯和伊布里奇，2019）领域已证明具有实用价值。将其调整用于为医疗器械提供保守估计，是一个有前景的未来机遇。

除了器械材料考量外，若能进一步了解可浸出物在植入物周围组织中的传输特性，也可能提高暴露预测的临床相关性。例如，如果组织中传输的对流贡献可以忽略不计，则浸出可能受到可浸出物在组织中的溶解度和扩散系数（分别为 $ S_T $ 和 $ D_T $）的限制。从数学上考虑这些因素相当于再次在方程1中用一个有效扩散系数 $ D_e $ 替代 $ D $，在此情况下，该有效扩散系数由（甘代克，1986）给出：

$$
D_e = \left( \frac{S_T D_T}{S_T D_T + S D} \right)^2 D
$$

因此，如果可浸出物在组织中溶解度足够低，或从器械‐组织界面缓慢迁移，则总体释放速率将相应降低。尽管这些组织特性可能难以确定，但可以利用体内（Wataha 等，2001）或离体（赛勒等人，2018；塞勒、索内森、克莱内德勒、霍纳和沃伦，2015）吸附数据进行评估和分析。图4展示了镍在各种组织中的特性的示例。

先前模型中隐含的一个假设是基质材料在体内不会发生溶胀或降解 in vivo。然而，许多器械应用所采用的材料在设计上会溶胀（佩帕斯、希尔特、卡迪姆侯赛尼和兰格，2006）和/或降解（徐、金、塞勒和库，2017）。在这种情况下，除了需考虑可浸出物的传输外，还必须考虑溶胀的程度和速率，以及材料降解过程中性能的变化。此外，如果发生显著溶胀，则不能忽略对流贡献的影响。

摘要

我们已经介绍了近期在应用基于物理的模型以提高暴露预测的临床相关性方面的努力，这些预测可支持毒理学风险评估。实施这些模型的主要挑战在于可用于参数化与验证的数据缺乏。尽管这在很大程度上限制了能够预测临床使用场景的暴露模型的发展，但基于保守假设和参数估计的保护性模型仍可作为常规筛选工具加以利用。如果拥有系统特异性数据，可用于量化材料或植入物周围组织环境中相关的传输特性，则预测结果的临床相关性可得到显著提升。采用数学与计算型基于物理的模型获得最大暴露剂量估计，其增强的临床相关性也可能适用于在体内倾向于溶胀或降解的器械材料。由于通常无法进行患者暴露的直接临床评估，因此，为更好地应对可浸出物相关的毒性担忧，改进毒理学风险评估方法的最佳途径是进一步开发、参数化并验证数学与计算型基于物理的模型，以预测患者暴露。