自适应传感器融合导航

相机、全球导航卫星系统和惯性测量单元的自适应传感器融合用于自动驾驶导航

摘要

视觉‐惯性导航系统（VINS）已成为无人机（UAV）或机器人技术领域中一种流行的导航方法。然而，其在自动驾驶场景下的性能并不理想，原因是自动驾驶场景比无人机场景更具挑战性和动态性。因此，视觉‐惯性导航系统偶尔会失效，从而影响导航结果。本文提出了一种自适应机制，可在三种模式之间切换：仅VINS、仅GNSS和视觉‐惯性与全球导航卫星系统融合。当视觉‐惯性组件失效时，我们的算法可仅依赖GNSS信号，直至VINS恢复；类似地，当GNSS信号不够精确时，系统可仅依赖VINS‐Mono。我们在夜间场景和高速公路等具有挑战性的场景下验证了该算法，并进行了定性分析和定量分析。

关键词

传感器融合，自适应机制，全球导航卫星系统，视觉‐惯性

一、引言

准确且鲁棒的导航系统是自动驾驶车辆的关键模块。目前，全球导航卫星系统（GNSS）仍然是组合导航系统中提供全球参考定位的主要手段[1]。随着实时动态定位（RTK）[2]的普及，GNSS在开阔区域可提供厘米级精度的定位结果。然而，大多数商用GNSS接收机仅能提供低频定位结果，且易受外部环境影响。惯性导航系统（INS）可通过惯性测量单元（IMU）采集的加速度和角速度测量值[3]，提供高频的六自由度位姿估计。但由于IMU测量误差会随时间累积[4]，INS无法独立支持长期导航。鉴于两者具有互补特性，GNSS与INS通常基于信息融合算法进行集成，以提高定位的精度和鲁棒性。一些企业如U‐blox、Novatel、OXTS已将GNSS/INS组合导航系统投入大规模生产。同时，GNSS/INS已成为自动驾驶车辆的主要定位模块[5]。

然而，在城市环境中，仅依赖GNSS/INS导航仍难以获得高精度的定位估计。由于GNSS信号被周围建筑物和动态物体遮挡或反射[6]–[8]，多路径效应和非视距信号（NLOS）接收经常发生。为提升车载导航系统在城市区域的性能，当前的研究方向包括：1）开发GNSS测量预处理方案，以削弱GNSS异常值的影响；2）开发更优的组合融合算法，融合更多传感器信息，如图像、激光雷达点、先验高精地图等。鉴于车载相机成本较低且计算机视觉技术快速发展，全球导航卫星系统/惯性测量单元/视觉融合正受到越来越多的关注，以提升车载组合导航系统的精度和鲁棒性。

本文主要关注全球导航卫星系统、惯性测量单元和图像这三种传感器信息的融合方案与算法。最常见的策略是采用基于滤波的方法的松耦合系统，其中视觉里程计（VO）作为一个独立系统运行，提供相对位姿估计。视觉里程计（VO）是指利用车辆上安装的相机所捕获的图像序列来估计无人驾驶车辆自我运动的过程[9]。与惯性导航系统和轮式里程计类似，VO通过分析车辆运动对其车载相机图像造成的变化，逐步估算车辆的位姿。关于基于视觉的状态估计/里程计/同步定位与地图构建的研究成果十分丰富。一些优秀的开源项目包括PTAM[10], SVO[11], LSD‐SLAM[12], DSO[13], 和ORB‐SLAM[14]。已有研究表明，与轮式里程计相比，VO能提供更精确的轨迹估计，相对位置误差在0.1%到0.2%之间[15]。因此，VO能够成为GNSS/INS组合导航系统的一个良好补充。

与紧耦合集成相比，松耦合集成由于状态向量的维度较小且方案更简单，更容易实现。但图像质量容易受到外部环境的影响。

环境，这将导致视觉里程计系统不准确或失效。在这种情况下，视觉里程计模块的不准确位姿估计很容易导致松耦合导航系统的性能下降。

为了提高视觉里程计系统（VO system）的精度和鲁棒性，近年来出现了视觉惯性里程计(VIO)。从VIO算法框架的角度来看，它可以分为两类：基于滤波的VIO和基于优化的VIO。一种经典的开源VIO——MSCKF[16]，是基于扩展卡尔曼滤波的。MSCKF通过引入IMU测量，显著提升了视觉里程计的性能。相比之下，基于优化的VIO通过将问题转化为基于IMU和视觉测量值的优化问题，从而获得最优的位姿估计。通常情况下，该方法相比基于滤波的方法可以获得更高的位姿估计精度，但需要更多的处理时间。VINS‐Mono[17]是最流行的开源VIO系统之一，在KITTI数据集[18]上取得了良好的成绩。

VINS‐Mono将IMU测量残差和视觉测量残差引入滑动窗口优化方案，实现IMU与视觉的紧耦合融合。因此，VINS‐Mono只能提供局部相对位姿估计，这对于自动驾驶车辆而言可能不够充分。VINS‐fusion是VINS‐Mono的扩展版本，融合了全局位置信息。基于VINS‐fusion，我们使用公开的城市交通数据集UrbanNav[19]和UrbanLoco[20]对该算法进行了测试。然而，在某些情况下结果并不十分理想。由于自动驾驶场景更具挑战性和动态性，VINS‐Mono偶尔会出现失效，从而影响导航性能。

在本研究中，我们引入全球导航卫星系统信号来辅助视觉惯性导航系统，并提出了一种新颖的自适应机制，使得整个导航算法在视觉惯性导航系统失效时能够仅依赖GNSS信号进行导航。我们在一些具有挑战性的场景（如夜间场景和高速公路）中验证了我们的算法。该算法能够有效检测视觉惯性导航系统的失效，并利用GNSS信号进行导航，直至视觉惯性导航系统成功重启。我们的主要贡献包括：提出一种自适应机制，在视觉惯性导航系统失效时利用全球导航卫星系统信号进行导航；引入滑动窗口以减少计算负载；在具有挑战性的场景中演示我们的算法，并进行定性和定量分析。

II. 系统概述

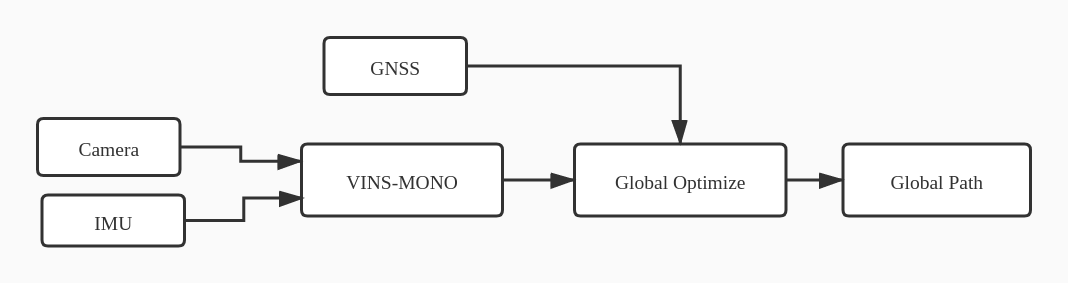
我们的系统主要基于VINS‐Fusion[21]。我们系统的结构如图1所示，选择VINS‐Mono作为我们的视觉惯性里程计算法。接收来自相机和惯性测量单元的数据，并将估计路径输出到全局融合节点。同时，全局融合节点将以较低频率接收来自全球导航卫星系统的数据。最后，全局融合节点将融合两条路径并输出全局路径。

III. 方法论

A. 位姿图结构

整个导航问题可以建模为图2所示的位姿图。每个节点包含一个六自由度位姿，对应于视觉惯性里程计的一次单次测量值。考虑到视觉惯性里程计在短时间内具有较高的精度，我们在两个节点之间添加视觉惯性测量作为相对约束。此外，当某个节点具有对应的GNSS测量值时，将添加GNSS约束作为全局约束。由于GNSS测量值不包含累积误差，且我们仅使用两个视觉惯性测量之间的相对位姿，因此该方法能够有效缓解累积误差。

位姿图优化问题可以通过最大后验估计（MAP）方法求解。假设所有的测量值都是独立的，则最大后验估计（MAP）可表示为，

$$
\hat{\chi} = \arg \max_{\chi} \prod_{t \in W} \prod_{k \in S} p(z_{kt}|\chi)
$$

其中，$\chi = {x_0, x_1, …, x_n}$, $x_i = {p_w^i, q_w^i}$, $p_w^i$ 和 $q_w^i$ 为位置向量和姿态四元数。W表示滑动窗口集，S是所有测量值的集合，包括视觉惯性和全球导航卫星系统。进一步地，若假设 $p(z_{kt}|\chi)$ 的分布为高斯分布，则原始MAP问题(1)可表示为，

$$
\hat{\chi} = \arg \max_{\chi} \prod_{t \in W} \prod_{k \in S} \exp\left(-\frac{1}{2} | z_{kt} - h_{kt}(\chi) |^2_{\Omega_{kt}}\right) = \arg \min_{\chi} \sum_{t \in W} \sum_{k \in S} | z_{kt} - h_{kt}(\chi) |^2_{\Omega_{kt}}
$$

其中 $\Omega_{kt}$ 表示高斯分布 $p(z_{kt}|\chi)$ 的信息矩阵，而 $h_{kt}(\chi)$ 是传感器模型。因此，整个导航问题已被表示为一个非线性优化问题。

B. 自适应机制

由于自动驾驶场景极具挑战性，有时VINS‐Mono会出现故障并偶尔重启。我们设计了一种自适应机制，当VINS‐Mono发生故障时，可仅依赖GNSS信号进行导航。当VINS‐Mono恢复后，VI因子将再次被添加到位姿图中。类似地，当协方差超过一定阈值时，我们会拒绝使用GNSS信号，仅依靠VINS‐Mono进行导航。

VINS‐Mono的失效将通过伪代码算法1中连续两帧t‐1和t之间的相对平移或旋转来检测，其中$(p_{VI}^{t-1}, q_{VI}^{t-1})$ 和 $(p_{VI}^t, q_{VI}^t)$ 是我们在时刻t从视觉惯性（VI）获得的位姿，$\ominus$ 表示四元数减法。因此，我们通过以下方式定义VINS自适应因子$\Phi$：

$$
\Phi =
\begin{cases}
0 & \text{if } \text{isVinsFail returns } 1 \
1 & \text{otherwise}
\end{cases}
$$

类似地，如果与GNSS信号相关的协方差大于某个阈值 $Cov_{threshold}$，我们也定义全球导航卫星系统自适应因子 $\Psi$。

$$
\Psi =
\begin{cases}
0 & \text{if } Cov_{GNSS} > Cov_{threshold} \
1 & \text{otherwise}
\end{cases}
$$

在两种自适应因子的帮助下，位姿图问题2可以表示为：

$$
\hat{\chi} = \arg \min_{\chi} \sum_{t \in W} \Phi \cdot | z_{VI}^t - h_{VI}^t(\chi) |^2_{\Omega_{VI}^t} + \Psi \cdot L_\delta(| z_{GNSS}^t - h_{GNSS}^t(\chi) |^2_{\Omega_{GNSS}^t})
$$

此外，为了减轻GNSS测量中异常值的影响，我们引入了具有鲁棒Huber核的M估计器 $L_\delta$，即

$$
L_\delta(a) =
\begin{cases}
\frac{1}{2} a^2 & \text{for } |a| \leq \delta \
\delta(|a| - \frac{1}{2}\delta) & \text{otherwise}
\end{cases}
$$

因此，我们的系统能够检测VINS的故障，并在三种模式之间切换：仅VINS‐Mono、仅GNSS以及VINS‐Mono与GNSS融合。在接下来的章节中，我们将定义公式(5)中的VI因子和GNSS因子。

C. 视觉-惯性因子

我们采用VINS‐Mono[17]来估计位姿作为我们的视觉‐惯性因子，该方法可提供六自由度位姿。考虑两个连续的帧$t$和帧$t - 1$，视觉‐惯性因子定义为：

$$
z_{VI}^t - h_{VI}^t(\chi) = z_{VI}^t - h_{VI}^t(x_{t-1}, x_t) =
\begin{bmatrix}
\alpha q_{VI}^{t-1}(p_{VI}^t - p_{VI}^{t-1}) - \alpha q_W^{t-1}(p_W^t - p_W^{t-1}) \
\beta(q_{VI}^{t-1} \ominus q_{VI}^t)(q_W^{t-1} \ominus q_W^t)
\end{bmatrix}
$$

其中 $\alpha$ 和 $\beta$ 是两个超参数，用于调节位置残差和旋转残差之间的权重。

D. GNSS因子

我们使用原始GNSS测量值中的经度、纬度和海拔，并将其转换为本地东‐北‐天(ENU)坐标。考虑到车辆通常从静止状态开始，我们在车辆静止时取平均GNSS测量值作为原点。GNSS因子定义为：

$$
z_{GNSS}^t - h_{GNSS}(\chi) = z_{GNSS}^t - h_{GNSS}(x_t) = p_{GNSS}^t - p_w^t
$$

其中 $p_{GNSS}^t = [x_w^t, y_w^t, z_w^t]^T$ 表示来自GNSS信号的测量值，我们直接使用原始GNSS数据中的协方差，该协方差表示可用卫星数量。

E. 优化

我们使用Ceres Solver[23]来求解公式(5)中提到的优化问题。Ceres求解器是一个开源的非线性优化工具，广泛应用于同步定位与地图构建领域。Ceres实现了许多经典的优化算法，其中我们选择Levenberg‐Marquardt方法来求解该非线性优化问题。

每次将新的全球导航卫星系统数据与相应的视觉惯性测量关联时，都会触发一次全局优化过程。如公式(5)所述，我们引入滑动窗口以降低计算负载，并确保系统能够实时运行。

IV. 实验

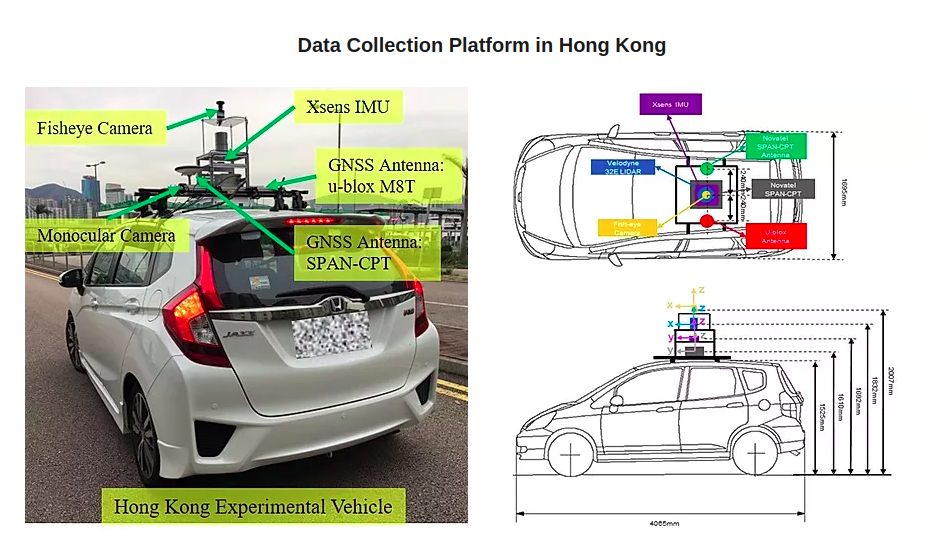
(a) UrbanNav 平台设置
(b) UrbanLoco 平台设置

为了验证我们提出的自动驾驶车辆方法的有效性，我们选择了开源数据集UrbanNav和UrbanLoco来测试我们的系统，这些数据集提供了包括夜间场景、高速公路等在内的具有挑战性的场景。所有的轨迹分析均由EVO[22]完成，该工具能够分析轨迹并输出RTE（相对轨迹误差）、中位数误差和平均误差等统计结果。

A. 数据集介绍

UrbanNav和UrbanLoco数据集中所使用的无人驾驶车辆外观如图3所示，其上安装了多种传感器，包括一个INS/IMU（Xsens‐Mti10）、一个多GNSS接收器（u‐blox M8T）、一个3D激光雷达传感器以及一些单目相机。真实值由Novatel SPAN‐CPT（高端RTK GNSS/INS组合导航系统）提供。我们在两个数据集的若干序列上运行了算法，以验证其有效性。

B. 定性分析

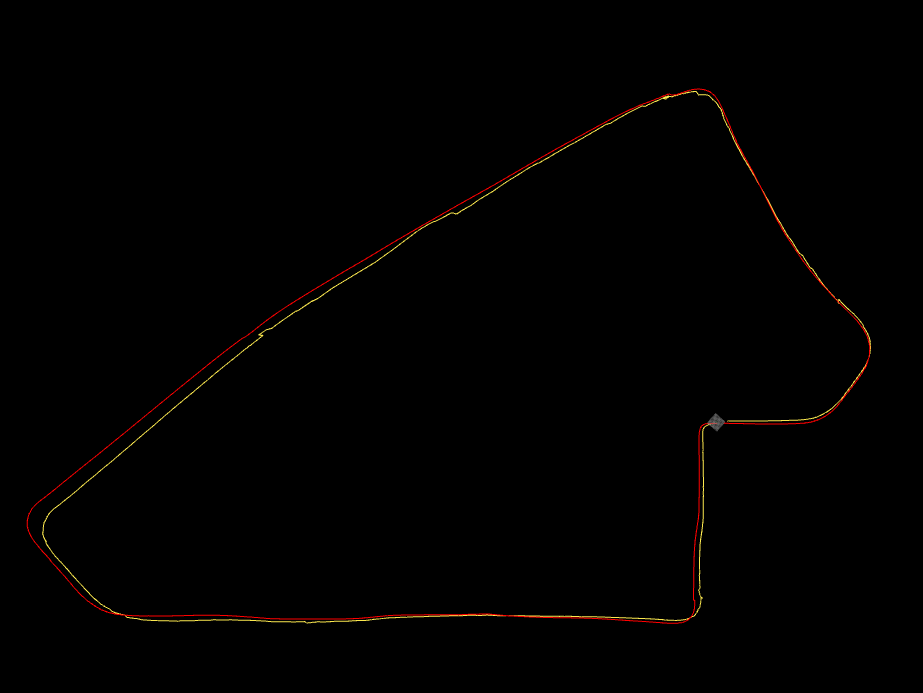
在本节中，我们在UrbanNav和UrbanLoco数据集的两个具有挑战性的场景中验证我们的自适应机制，并对其进行定性分析。在本小节中，我们向真实值信号添加高斯噪声以模拟GNSS信号，高斯噪声的标准差设为5米。结果如图4所示。在图4中，红线表示真实值，黄线表示估计路径。由于VINS‐Mono多次失效，我们未显示其路径。

表I 定性分析数据

数据集	VINS崩溃次数	轨迹长度	持续时间
UrbanLoco01	6	13.14公里	930s
UrbanNav01	4	2.01公里	488s

VINS‐Mono崩溃的次数、轨迹长度以及测试持续时间如表I所示。UrbanLoco01是在加利福尼亚记录的一段高速公路场景。在此期间，由于车辆速度较高，VINS‐Mono共崩溃6次。此外，当VINS‐Mono发生故障时，由于缺乏足够的特征点，重启需要较长时间。因此，在VINS‐Mono失效时，有必要引入自适应机制以实现导航。轨迹如图4(b)所示。UrbanLoco01序列总长度为13.14公里，总时长为930秒，可验证我们的算法在长时间运行中的有效性。

UrbanNav序列01记录了香港的夜间场景城市环境，其中特征点不稳定，导致VINS‐Mono崩溃了4次。从图4(b)可以看出，我们的算法能够有效检测VINS‐Mono的失效，并在VINS‐Mono失效时继续导航。

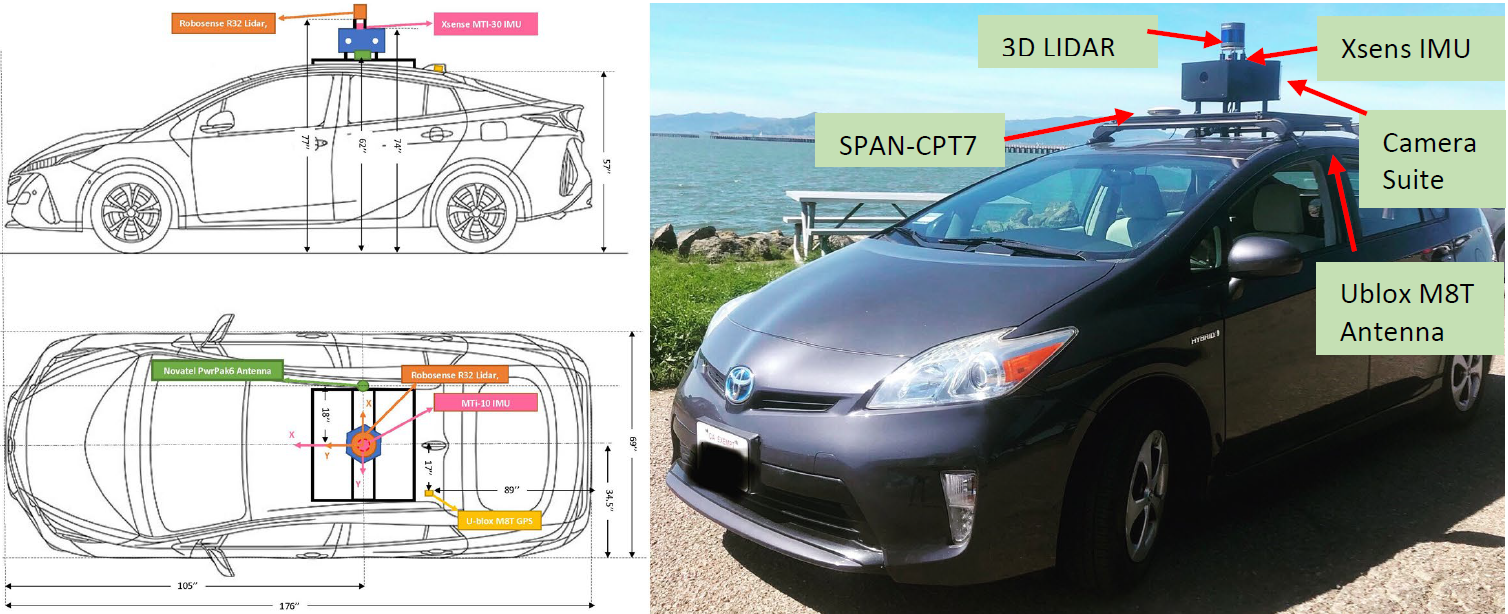
(a) UrbanLoco 序列01
(b) UrbanNav序列01

C. 定量分析

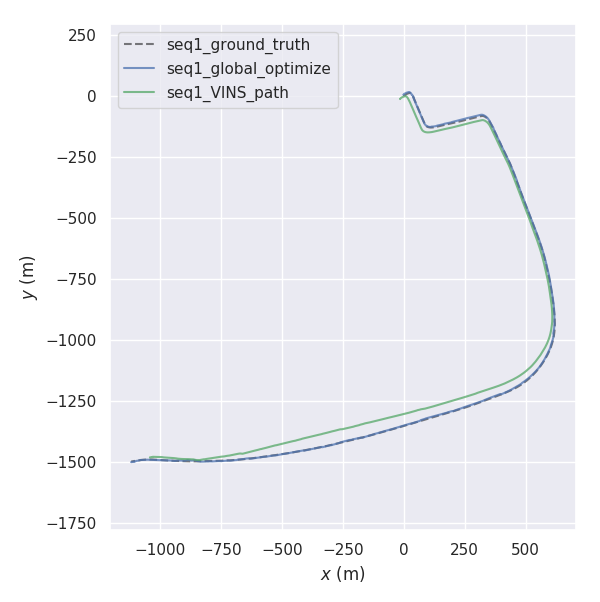
在本小节中，我们首先通过向真实值添加高斯噪声来演示我们的算法，然后加入真实的GNSS信号。当我们使用高斯噪声时，高斯噪声的标准差选择为5米。轨迹如图5所示，以及误差之间的

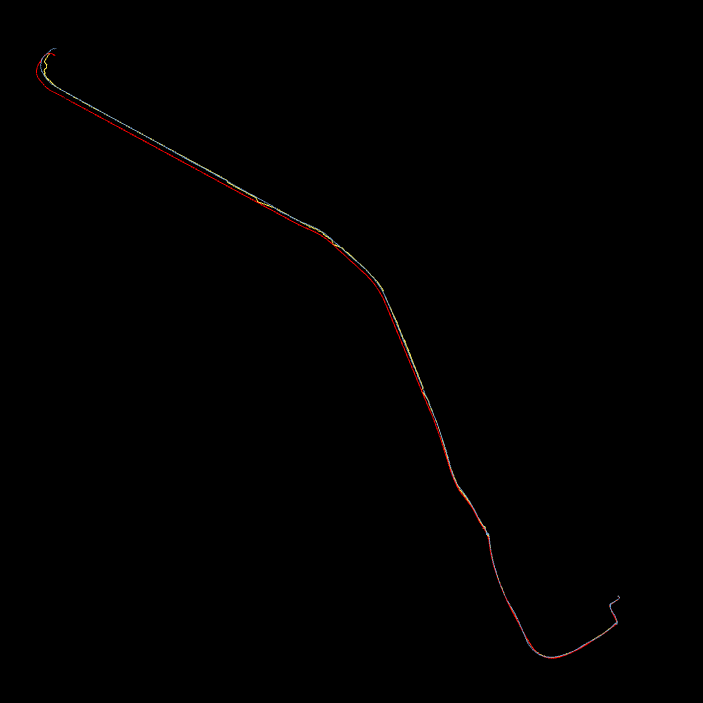
(a) UrbanLoco 序列01
(b) UrbanNav序列01

真实值和估计路径如图6所示。定量结果总结于表II中。

(a) UrbanLoco 序列01
(b) UrbanNav序列01

表II 定量分析数据

序列	最大误差(米)	平均误差(米)	中位误差(米)
序列1	35.30	7.31	5.22
序列2	33.80	9.00	8.39

从图5可以看出，在加入GNSS信号（绿线）之前，误差会累积。此外，当车辆进行匀速运动时，恢复的尺度会出现错误。加入GNSS信号后，这两种现象得到缓解（蓝线），正如图5所示。加入GNSS后，误差显著降低。进一步地，真实轨迹与估计路径之间的误差如表II所示。加入GNSS信号后，平均误差和中位误差均在10米以内，相对于整个轨迹的长度而言是可接受的。

然后我们加入真实的GNSS信号，使用UrbanNav 序列01来验证我们的算法，结果如图7所示。从图7(a)可以看出，平均误差为14.55米，中位数误差为12.42米。相对于总轨迹长度642米，相对误差约为2%。从图7(b)可以看出，误差主要来自X轴，而在YZ轴上的误差相对较小。考虑到车辆主要沿Y轴行驶，或许我们可以增加更多关于车辆运动的约束来拒绝未来的GNSS信号的异常值。

(a) 相对轨迹误差
(b) XYZ误差
(c) 轨迹

V. 结论

在本研究中，我们提出了一种自适应机制，利用GNSS信号辅助VINS系统，并引入滑动窗口以降低计算成本。当视觉惯性组件失效时，我们的算法可以仅依赖GNSS信号进行导航，直到VINS恢复。此外，我们的算法能够拒绝不可靠的GNSS信号。相对较大的协方差，并且仅在GNSS和VI两种信号都可靠时才进行融合。我们在夜间场景和高速公路等具有挑战性的场景下验证了我们的算法，并进行了定性分析和定量分析。在定性分析部分，我们可以看到，当VINS‐Mono出现故障时，我们的算法能够有效检测到该故障，并在VINS‐Mono恢复之前依靠GNSS进行导航。在定量分析部分，我们证明了如果GNSS信号足够准确，我们的算法可以达到令人满意的精度。对于未来的工作，我们正在致力于解决自动驾驶车辆在匀速或平面运动时引起的尺度漂移问题。同时，我们也在尝试引入IMU信号对GNSS数据进行预处理，并拒绝其中的异常值。