1 相关工作
本文根据2015年《NICE: Non-linear Independent Components Estimation》翻译总结的。流模型的最初论文。流模型(flow)也是一种生成模型。
1)像deep Boltzmann machines (DBM,2009)无向图模型,其用采用Markov chain Monte Carlo (MCMC)而很慢。
2)variational auto-encoders (VAE)(2014)使用随机encoder q(h|x)和不完美的decoder p(x|h),成本上需要一个重构项,保证decoder近似反转encoder。这注入了噪声到auto-encoder循环中,因为h是从q(h|x)采样的,其是对真正后验p(h|x)一个可变近似。训练的目标就是数据log-likelihood的可变下界(variational lower bound)。有向图提供的一般化的快速的原始采样技术使得VAE模型非常吸引人。但是使用lower bound对于真正的log-likelihood是次优的。如此次优的方案也许会在生成过程中注入显著的非结构化噪声。
NICE模型是学习一个非线性双射转换(bijective transformation),其将训练数据映射到另一个空间,在该空间上分布是可以因子化的,整个模型架构依靠直接最大化log-likelihood来完成。
2 简介
非监督学习的主要问题之一是如何捕捉复杂的数据分布,其结构未知。深度学习方法(bengio,2009)依靠数据表达的学习,其捕捉变量最重要的因子。这就带来一个问题:什么是一个好的表达(representation)?我们认为一个好的表达是其数据分布很容易建模。

利用change of variable方法。
对于h=f(x),我们假定f是可逆的,h的维度和x的一样。

本文的主要创新就是f,其有两个属性,一个是雅可比矩阵的容易行列式,一个是容易可逆。其容许我们有足够的容量学习复杂的变换。

3 学习连续概率的双射变换
使用maximum likelihood。

同时这个先验分布如果各维度独立,可以因子化,故可以写成下式,从而获得了我们的non-linear independent components estimation (NICE)。
我们可以将NICE视为学习数据集的可逆预处理变换。
在以前的variational auto-encoder (Kingma and Welling, 2014; Rezende et al., 2014; Mnih and Gregor, 2014; Gregor et al., 2014), 我们可以称f为encoder,f的逆为decoder。
4 结构
4.1 三角形结构
针对f,我们采用三角形雅可比矩阵。
4.2耦合层
我们描述一个双射变换(bijective transformation),其拥有三角形雅可比矩阵,所以是易计算的。
一般的耦合层:
其实就是第2章提到的函数m,即耦合函数m构造耦合层。
其中g可以是任何形式的,我们采用加法形式,g(a;b)=a+b.
耦合层一般至少3层,才能容易所有的维度互相影响。我们采用了4层。
4.3 先验分布
可以采用高斯分布:
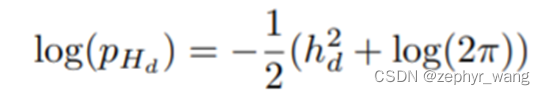
或者逻辑分布:
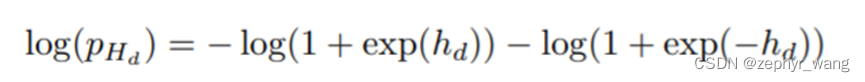
我们倾向于使用逻辑分布,其倾向于提供更好的梯度。
5 实验
可以看到NICE表现更好。
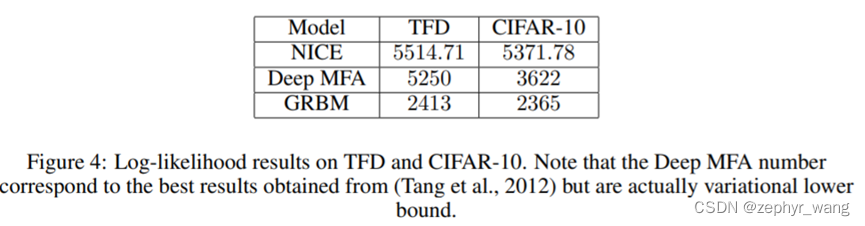





 NICE模型是一种通过学习非线性双射变换实现数据分布建模的方法。它将数据映射到一个易于因子化的空间,并通过直接最大化log-likelihood进行训练。与VAE不同,NICE避免了使用可变下界,减少了生成过程中的非结构化噪声。
NICE模型是一种通过学习非线性双射变换实现数据分布建模的方法。它将数据映射到一个易于因子化的空间,并通过直接最大化log-likelihood进行训练。与VAE不同,NICE避免了使用可变下界,减少了生成过程中的非结构化噪声。

















 1752
1752

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








