广度优先搜索（BFS）算法（图文并茂，新手必看）

广度优先搜索（Breadth First Search）简称广搜或者 BFS，是遍历图存储结构的一种算法，既适用于无向图（网），也适用于有向图（网）。

所谓图的遍历，简单理解就是逐个访问图中的顶点，确保每个顶点都只访问一次。

首先通过一个样例，给大家讲解广度优先搜索算法是如何实现图的遍历的。

图 1 广度优先搜索算法遍历图

使用广度优先搜索算法，遍历图 1 中无向图的过程是：
1) 初始状态下，图中所有顶点都是尚未访问的，因此任选一个顶点出发，开始遍历整张图。

比如从 V1 顶点出发，先访问 V1：

图 2 访问顶点 V1

2) 从 V1 出发，可以找到 V2 和 V3，它们都没有被访问，所以访问它们：

图 3 访问 V2 和 V3

注意：本图中先访问的是 V2，也可以先访问 V3。当可以访问的顶点有多个时，访问的顺序是不唯一的，可以根据找到各个顶点的先后次序依次访问它们。后续过程也会遇到类似情况，不再重复赘述。

3) 根据图 3 中的顶点访问顺序，紧邻 V1 的顶点已经访问过，接下来访问紧邻 V2 的顶点。

从 V2 顶点出发，可以找到 V1、V4 和 V5，尚未访问的有 V4 和 V5，因此访问它们：

图 4 访问 V4 和 V5

4) 根据图 4 中的顶点访问顺序，接下来访问紧邻 V3 的顶点。

从 V3 顶点出发，可以找到 V1、V6 和 V7，尚未访问的有 V6 和 V7，因此访问它们：

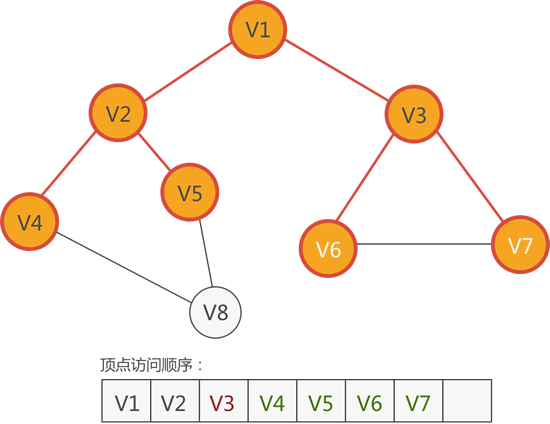
图 5 访问 V6 和 V7

5) 根据图 5 中的顶点访问顺序，接下来访问紧邻 V4 的顶点。

从 V4 顶点出发，可以找到 V2 和 V8，只有 V8 尚未访问，因此访问它：

图 6 访问 V8

6) 根据图 6 的顶点访问顺序，接下来访问紧邻 V5 的顶点。

观察图 6 中的无向图不难发现，与 V5 紧邻的 V2 和 V8 都已经访问过，无法再找到尚未访问的顶点。此时，广度优先搜索算法会直接跳过 V5，继续从其它的顶点出发。

7) 广度优先搜索算法先后从 V6、V7、V8 出发，寻找和它们紧邻、尚未访问的顶点，但寻找的结果都和 V5 一样，找不到符合要求的顶点。

8) 自 V8 之后，访问序列中再无其它顶点，意味着从 V1 顶点出发，无法再找到尚未访问的顶点。这种情况下，广度优先搜索算法会从图的所有顶点中重新选择一个尚未访问的顶点，然后从此顶点出发，以同样的思路继续寻找其它尚未访问的顶点。

本例中的无向图是一个连通图，从 V1 出发可以找到所有的顶点，因此广度优先搜索算法继 V1 顶点之后无法再找到新的尚未访问的顶点，算法执行结束。

对于连通图来说，广度优先搜索算法从一个顶点出发就能访问图中所有的顶点。但是对于非连通图来说，广度优先搜索算法必须从各个连通分量中选择一个顶点出发，才能访问到所有的顶点。

广度优先搜索算法的具体实现

所谓广度优先搜索，就是从图中的某个顶点出发，寻找紧邻的、尚未访问的顶点，找到多少就访问多少，然后分别从找到的这些顶点出发，继续寻找紧邻的、尚未访问的顶点。

当从某个顶点出发，所有和它连通的顶点都访问完之后，广度优先搜索算法会重新选择一个尚未访问的顶点（非连通图中就存在这样的顶点），继续以同样的思路寻找未访问的其它顶点。直到图中所有顶点都被访问，广度优先搜索算法才会结束执行。

图的存储结构有很多种，大体上可以分为顺序存储和链式存储（又细分为邻接表结构、十字链表结构和邻接多重表结构），各个存储结构有自己的特点。选用不同的存储结构，广度优先搜索算法的具体实现不同，但算法的思想是不变的。

这里以图的顺序存储结构为例，广度优先搜索算法的 C 语言实现代码如下：

#include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20                   //顶点的最大数量
#define VRType int                          //表示顶点之间关系的数据类型
#define VertexType int                      //顶点的数据类型
typedef enum { false, true }bool;           //定义bool型常量
bool visited[MAX_VERtEX_NUM];               //设置全局数组，记录每个顶点是否被访问过

//队列链表中的结点类型
typedef struct Queue {
    VertexType data;
    struct Queue* next;
}Queue;

typedef struct {
    VRType adj;                             //用 0 表示不相邻，用 1 表示相邻
}ArcCell, AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];

typedef struct {
    VertexType vexs[MAX_VERtEX_NUM];        //存储图中的顶点
    AdjMatrix arcs;                         //二维数组，记录顶点之间的关系
    int vexnum, arcnum;                     //记录图的顶点数和弧（边）数
}MGraph;

//判断 v 顶点在二维数组中的位置
int LocateVex(MGraph* G, VertexType v) {
    int i;
    //遍历一维数组，找到变量v
    for (i = 0; i < G->vexnum; i++) {
        if (G->vexs[i] == v) {
            break;
        }
    }
    //如果找不到，输出提示语句，返回-1
    if (i > G->vexnum) {
        printf("no this vertex\n");
        return -1;
    }
    return i;
}

//构造无向图
void CreateDN(MGraph* G) {
    int i, j, n, m;
    int v1, v2;
    scanf("%d,%d", &(G->vexnum), &(G->arcnum));
    for (i = 0; i < G->vexnum; i++) {
        scanf("%d", &(G->vexs[i]));
    }
    for (i = 0; i < G->vexnum; i++) {
        for (j = 0; j < G->vexnum; j++) {
            G->arcs[i][j].adj = 0;
        }
    }
    for (i = 0; i < G->arcnum; i++) {
        scanf("%d,%d", &v1, &v2);
        n = LocateVex(G, v1);
        m = LocateVex(G, v2);
        if (m == -1 || n == -1) {
            printf("no this vertex\n");
            return;
        }
        G->arcs[n][m].adj = 1;
        G->arcs[m][n].adj = 1;
    }
}

int FirstAdjVex(MGraph G, int v)
{
    int i;
    //对于数组下标 v 处的顶点，找到第一个和它相邻的顶点，并返回该顶点的数组下标
    for (i = 0; i < G.vexnum; i++) {
        if (G.arcs[v][i].adj) {
            return i;
        }
    }
    return -1;
}

int NextAdjVex(MGraph G, int v, int w)
{
    int i;
    //对于数组下标 v 处的顶点，从 w 位置开始继续查找和它相邻的顶点，并返回该顶点的数组下标
    for (i = w + 1; i < G.vexnum; i++) {
        if (G.arcs[v][i].adj) {
            return i;
        }
    }
    return -1;
}

//初始化队列，这是一个有头结点的队列链表
void InitQueue(Queue** Q) {
    (*Q) = (Queue*)malloc(sizeof(Queue));
    (*Q)->next = NULL;
}

//顶点元素v进队列
void EnQueue(Queue** Q, VertexType v) {
    Queue* temp = (*Q);
    //创建一个存储 v 的结点
    Queue* element = (Queue*)malloc(sizeof(Queue));
    element->data = v;
    element->next = NULL;
    //将 v 添加到队列链表的尾部
    while (temp->next != NULL) {
        temp = temp->next;
    }
    temp->next = element;
}

//队头元素出队列
void DeQueue(Queue** Q, int* u) {
    Queue* del = (*Q)->next;
    (*u) = (*Q)->next->data;
    (*Q)->next = (*Q)->next->next;
    free(del);
}

//判断队列是否为空
bool QueueEmpty(Queue* Q) {
    if (Q->next == NULL) {
        return true;
    }
    return false;
}

//释放队列占用的堆空间
void DelQueue(Queue* Q) {
    Queue* del = NULL;
    while (Q->next) {
        del = Q->next;
        Q->next = Q->next->next;
        free(del);
    }
    free(Q);
}

//广度优先搜索
void BFSTraverse(MGraph G) {
    int v, u, w;
    Queue* Q = NULL;
    InitQueue(&Q);
    //将用做标记的visit数组初始化为false
    for (v = 0; v < G.vexnum; ++v) {
        visited[v] = false;
    }
    //遍历图中的各个顶点
    for (v = 0; v < G.vexnum; v++) {
        //若当前顶点尚未访问，从此顶点出发，找到并访问和它连通的所有顶点
        if (!visited[v]) {
            //访问顶点，并更新它的访问状态
            printf("%d ", G.vexs[v]);
            visited[v] = true;
            //将顶点入队
            EnQueue(&Q, G.vexs[v]);
            //遍历队列中的所有顶点
            while (!QueueEmpty(Q)) {
                //从队列中的一个顶点出发
                DeQueue(&Q, &u);
                //找到顶点对应的数组下标
                u = LocateVex(&G, u);
                //遍历紧邻 u 的所有顶点
                for (w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)) {
                    //将紧邻 u 且尚未访问的顶点，访问后入队
                    if (!visited[w]) {
                        printf("%d ", G.vexs[w]);
                        visited[w] = true;
                        EnQueue(&Q, G.vexs[w]);
                    }
                }
            }
        }
    }
    DelQueue(Q);
}
int main() {
    MGraph G;
    //构建图
    CreateDN(&G);
    //对图进行广度优先搜索
    BFSTraverse(G);
    return 0;
}

程序中，广度优先搜索算法的实现借助了队列存储结构，用来存储访问过的顶点。每次出队一个顶点，从该顶点出发寻找和它紧邻、尚未访问的顶点，然后将找到的顶点全部入队。

用 1~8 分别表示图 1 中的顶点 V1~V8，程序的执行结果为：

8,9
1
2
3
4
5
6
7
8
1,2
2,4
2,5
4,8
5,8
1,3
3,6
6,7
7,3
1 2 3 4 5 6 7 8

实现图的遍历，除了使用本节讲解的广度优先搜索算法外，还可以使用深度优先搜索算法，感兴趣的小伙伴可以猛击《深度优先搜索（DFS）算法》详细了解。